Случайные величины и их характеристика

Случайные величины и их характеристика

• Случайные величины и их характеристики До сих пор это была случайная проблема: Да нет, этого не произошло. Современная теория вероятностей В основном используются случайные величины. Случайная переменная является такой переменной. В результате опыта вы можете взять любое количество Значение, и о котором оно не известно.

• Например, отклонение Прибыль от ожидаемой стоимости. Случайные величины являются дискретными (прерывистыми) и Постоянно. Дискретная случайная величина Получить только отдельные изолированные значения Перечислено, что можно предвидеть. Например, ожидается Количество единиц: 0, 1, 2. Больше не Не может принять значение. Непрерывные случайные величины являются такими величинами.

Есть бесчисленное множество значений. Людмила Фирмаль

Например, возможная сумма прибыли. Для характеристики случайных величин Примените так называемый дистрибутив. Распределение-характеристика случайных величин, Показывает следующее: -Значение, которое может принимать случайная величина. Одна или другая возможность этих значений. Дискретное распределение случайных величин Используются два типа групп случайных величин.

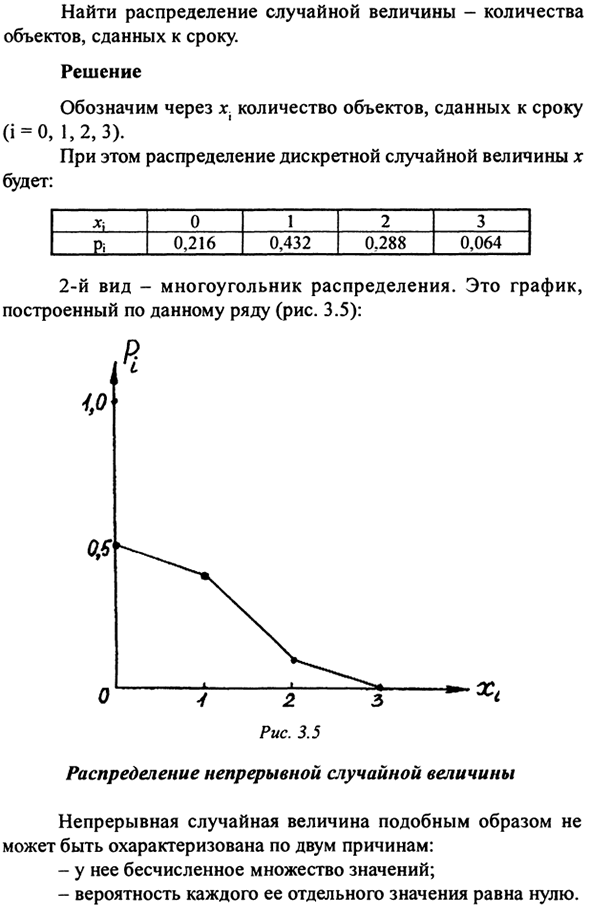
Распространение. Тип 1-Распределительная серия: х р Χι пирог * 2 Wg х-ы Rz … х „ … р „ Пример 3.27 Контракт на три идентичные конструкции Объект. Вероятность сдачи объекта во время р = 0,2. Найти распределение случайных величин Объект, который доставлен вовремя. Решения Указывает количество объектов, доставленных к сроку в г 0 = 0,1,2,3).

• Кроме того, распределение дискретной случайной величины χ Будете ли вы: запад Ιρ 0 0,216 1 0,432 2 0,288 3 0,064 I Второй вид-распределение полигонов. Это график Постройте эту строку (рисунок 3.5): Непрерывное распределение случайных величин Таким образом, непрерывная случайная величина Он характеризуется по двум причинам: -Она имеет бесчисленные значения.

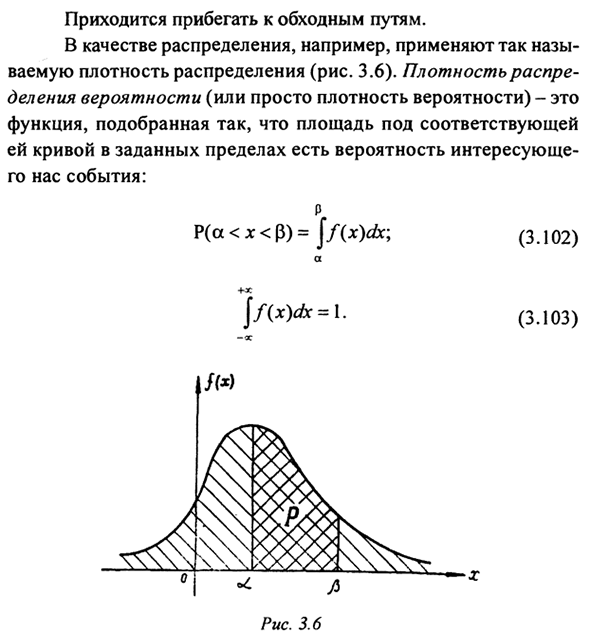
Вероятность каждого отдельного значения равна нулю. Вы должны положиться на обходной путь. Например, в качестве дистрибутива Это называется плотностью распределения (рис. 3.6). плотность Распределение вероятностей (или просто плотность вероятности) Соответствующая нижняя область.

Существует вероятность кривой в пределах данного предела Интересные события: Людмила Фирмаль

Смотрите также:

• Решение экономико математических методов

Теория вероятностей и математическая статистика. Основные понятия	Числовые характеристики случайных величин
Основные теоремы теории вероятностей	Законы распределения случайных величин