Оглавление:
Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, неизвестное заранее какое именно.
Будем обозначать случайные величины прописными буквами 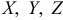 , и их возможные значения — соответствующими строчным буквами —
, и их возможные значения — соответствующими строчным буквами — 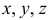 .
.
Дискретной называют случайную величину, которая принимает отдельные, возможные значения с определенной вероятностью. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.
Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка.
Число возможных значений непрерывной случайной величины бесконечно.
Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями.
Способы задания: таблично, аналитически, графически.
1). С помощью таблицы.

События 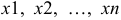 — образуют полную группу, т.е.
— образуют полную группу, т.е.  .
.
Такую таблицу называют рядом распределения случайной величины 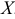 .
.
2) Графическое изображение.
Для наглядности точки соединяются отрезками прямых. Такая фигура называется многоугольником распределения.
Пример №1
Игральная кость брошена 3 раза. Написать закон распределения числа появлений шестерки.
Решение:
Вероятность появления шестерки при одном бросании 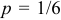 , вероятность не появления шестерки
, вероятность не появления шестерки 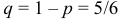 .
.
При трех бросаниях игральной кости шестерка может появиться либо 3 раза, либо 2 раза, либо 1 раз, либо совсем не появиться. Таким образом, возможные значения 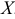 таковы:
таковы: 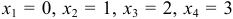 . Найдем вероятности этих возможных значений по формуле Бернулли:
. Найдем вероятности этих возможных значений по формуле Бернулли: 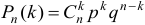 .
.
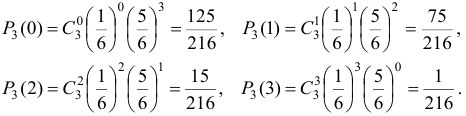
Искомый закон распределения:
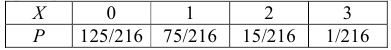
Если производится 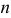 независимых испытаний, в каждом из которых событие
независимых испытаний, в каждом из которых событие 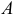 может появится либо не появиться, причем вероятность наступления события в каждом испытании постоянна и равна
может появится либо не появиться, причем вероятность наступления события в каждом испытании постоянна и равна 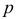 , то закон распределения вероятностей определяется формулой Бернулли:
, то закон распределения вероятностей определяется формулой Бернулли: 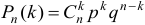 , которое называют биноминальным распределением вероятностей.
, которое называют биноминальным распределением вероятностей.
Запишем биноминальный закон в виде таблицы:

Если производится 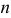 независимых испытаний, в каждом из которых вероятность появления события
независимых испытаний, в каждом из которых вероятность появления события 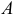 равно
равно 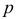 и
и 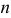 велико, то закон распределения вероятностей массовых (
велико, то закон распределения вероятностей массовых (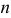 велико) и редких (
велико) и редких (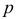 мало) событий определяется:
мало) событий определяется:
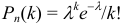 , где
, где 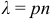 .
.
Эта формула выражает закон распределения Пуассона.
Пример №2
Прядильщица обслуживает 1000 веретен. Вероятность обрыва нити на одном веретене в течение 1 минуты равна 0,004. Найти вероятность того, что в течение 1 минуты обрыв произойдет на пяти веретенах.
Решение:
По условию 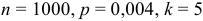 . Найдем
. Найдем 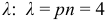 .
.
По формуле Пуассона искомая вероятность приближенно равна
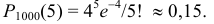
Рассмотрим события, которые наступают в случайные моменты времени.
Потоком событий называют последовательность событий, которые наступаю в случайные моменты времени.
Интенсивность потока 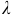 называют среднее число событий, которые появляются в единицу времени.
называют среднее число событий, которые появляются в единицу времени.
Если постоянная интенсивность потока известна, то вероятность появления 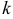 событий простейшего потока за время длительностью
событий простейшего потока за время длительностью 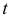 определяется формулой Пуассона
определяется формулой Пуассона
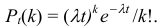
Простейшим (пуассоновским) называют поток событий, который обладает свойствами стационарности, отсутствия последействия и ординарности.
Свойство стационарности характеризуется тем, что вероятность появления 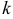 событий на любом промежутке времени зависит только от числа
событий на любом промежутке времени зависит только от числа 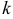 и от длительности
и от длительности 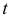 промежутка и не зависит от начала его отсчета; при этом промежутки времени предполагаются непересекающимися.
промежутка и не зависит от начала его отсчета; при этом промежутки времени предполагаются непересекающимися.
Свойство отсутствия последствия характеризуется тем, что вероятность появления 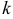 событий за промежуток времени длительности
событий за промежуток времени длительности 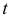 есть функция, зависящая только от
есть функция, зависящая только от 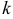 и
и 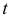 .
.
Свойство ординарности характеризуется тем, что появление двух и более событий за малый промежуток времени практически невозможно, т.е. за бесконечно малый промежуток времени может появиться не более одного события.
Пример №3
Среднее число вызовов, поступающих на АТС в 1 минуту, равно 5. найти вероятность того, что за две минуты поступит:
а) три вызова; б) менее трех вызовов.
Решение:
Будем предполагать, что поток вызовов является простейшим.
а) По условию 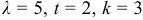 . Вероятность того, что за две минуты поступит два вызова найдем по формуле Пуассона:
. Вероятность того, что за две минуты поступит два вызова найдем по формуле Пуассона:
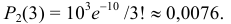
б) События не поступило ни одного вызова, поступил один вызов и поступило два вызова несовместны, поэтому по теореме сложения искомая вероятность того, что за две минуты поступит менее трех вызовов, равна
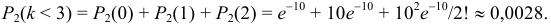
На этой странице размещён краткий курс лекций по теории вероятностей и математической статистике с теорией, формулами и примерами решения задач:
Теория вероятностей краткий курс для школьников и студентов
Возможно вам будут полезны эти страницы:

