Оглавление:

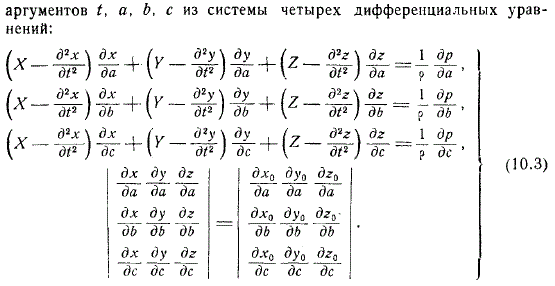

Несжимаемая жидкость
Несжимаемая жидкость, плотность это определенная константа, которая действует как физическое свойство определенного типа жидкости и считается известной. Если вы возьмете уравнение Эйлера (или ОЗУ) и гидромеханику, неизвестные величины-это 4 величины, которые зависят от каждого аргумента, но это заданные функции одного и того же аргумента.
Выглядит примерно вот так:
- dv x dt
- dv x dz
Если мы добавим общую постановку задач гидродинамики к 3 дифференциальным уравнениям Эйлера уравнение неразрывности, которое является 4-м дифференциальным уравнением, возникает проблема определения 4 неизвестных функций из системы 4 дифференциальных уравнений.
Если эта система может быть интегрирована, векторное поле скорости и скалярное поле давления в каждый момент времени определяются для нахождения функции, удовлетворяющей задаче. To выполнив и определив уравнение движения для каждой частицы, «временную зависимость координат частицы и ее зависимость от начальных значений координат», необходимо закрепить еще одну систему из 3 уравнений.
Определенная константа
Если взять уравнение движения в Лагранжевой форме аналогично, то в этом случае задача будет заключаться в определении 4 неизвестных функций, которые зависят от количества каждой. Выведем наиболее общие уравнения, связывающие равномерное течение несжимаемой жидкости с действующими на нее силами жидкость, выберите любой объем с площадью поверхности случайной сжимаемой жидкости. Баротропностью и бароклинностью. и уравнение притока энергии.
В пределах этого объема выберите основной объем с плотностью, массой и площадью поверхности. На объем воздействуют массовая (гравитационная) сила растяжения и поверхностные силы, обусловленные напряжением.
| Система 1 | Система 1 | Система 1 |
| У gt; z gt; о | s lt; i gt; о | H lt; w lt; о |
Ускорение центра тяжести основного объема можно описать в пункте следует отметить, что во многих задачах динамики уравнения механики жидкости идеальной жидкости широко используются, так как влиянием вязкости жидкости можно пренебречь или учесть расчёт станет произвольным. To выведя эти уравнения, мы используем общие уравнения движения для однородной несжимаемой невязкая жидкость, там нет напряжения сдвига.
При интегрировании дифференциального уравнения неразрывности с динамикой невязкой жидкости константа интегрирования появляется в зависимости от координаты. To определяя их, нужно использовать начальные и граничные условия задачи.
Начальные условия определяют кинематические и динамические свойства движения жидкости первого момента. Они имеют смысл только для нестационарных движений и в первый момент будут задавать положение границ, скорость, давление или другие параметры движения.

