Случай Лагранжа и Пуассона

Оглавление:

Случай Лагранжа и Пуассона

Для оси Oz возьмем ось вращения эллипсоида инерции в точку O, а для положительного направления этой оси примем направление OQ от начала координат O до центра тяжести. Тогда Л =В, = т =О С 0.Кроме того, поскольку С, С,=, иos 9, 6 являются углами между осями Oz и Ozv, давайте сначала посмотрим, какие инвариантные интегралы 44 и 45 будут. Теорема о кинетической энергии A p + P 4 Cr2 = 2MgC,+ L = 2Mg: cos 9 4 L. 46. Кроме того, мы пишем, что проекция главного импульса движения ОА на ось z является константой K. Затем вспомним формулы y, f , y в функциях 6 и p и получим их на основе уравнения 45.

Потому что БФ 4 КР, потому что 9 =к. 47 Присоедините уравнения Эйлера к этим 2 интегралам В этом случае он принимает следующий вид г = 0. л.,. 48 Потому что B A и N равны нулю. Эти 3 уравнения можно записать в виде: Р + 9 = а Бл 9. грех 9 Р грех P на 4 м, потому что ИС = br0, потому что 9 Где b положительные постоянные коэффициенты, соответственно C 0 Равно u, а a и p любые интегральные константы. Ниже мы предполагаем, что r0 не равно нулю.

Возьмем еще систему материальных точек, притягиваемых неподвижным центром О пропорционально массам и расстояниям г. Людмила Фирмаль

Если r0 = 0, то движение оси тела Oz совпадает с движением нити сферы маятника пункт 277. Углы ср, 9 и F связаны с P, Q и R на следующие отношения: Ф. 0. 46. Р sin9sin Р Джей Джей, потому что кф. F. На 46. Ж. Н. совместно. Т ам Р = РНЕ я Л Г ДТ, потому что о т ДТ Присвойте эти значения приведенному выше выражению, чтобы оно имело следующую форму EGSO5B + е г 49 50 51 52 За исключением первых 2 мы получаем уравнение 6: p br0 cos 6 + sin 9 = sin 9 A e cos 9. cos 9 = a. получаем = 1 гйи, у = F U. 2 е уравнение 49 принимает вид: 4рн 9 Б. dt = 1 ci и 3 й ДФ 4Ф 9 6g0a ДТ Р ДТ Р 1 а Многочлен f u отрицателен для значений co, 1, 4 1, u = 4 и положителен для начального значения u, a0.

Кроме того, если u = a0, то величина является реальной. Таким образом, многочлены имеют 3 вещественных корня: et, a2 и, соответственно, заключенные в интервалы. 1.А0. А0. 4 1.И 4 1, 4 ОО. Таким образом, вы можете написать: Ф У = А А а аа а а а Будучи Косинусом, последний фактор является очень положительным и всегда находится между 1 и 4 1. значение a, начинающееся с a0, всегда равно И так что остается положительным u2.As в результате угол b колеблется между 2 предельными углами 91 и 02 9 62, а его Косинус равен u1 и u. когда расти г = + K7w. если вы уменьшаете u от u2 до, Вам нужно поставить знак. Если у вас есть вершина O вокруг оси Ozt рис.

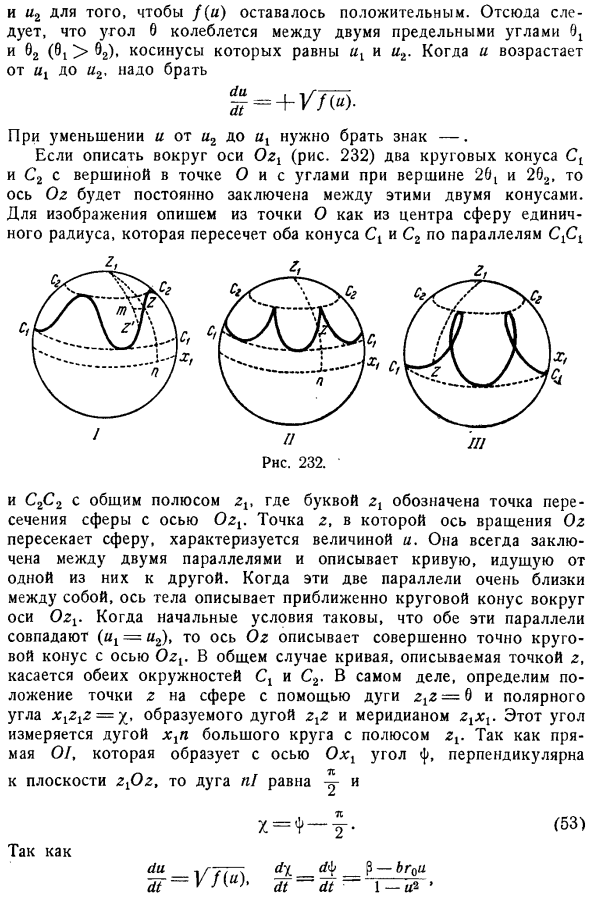
Описать 2 конических Ct и Cr с углами в вершинах 26t и 202, ось Oz всегда будет заключена между этими 2 cones. In на этом изображении, начиная с точки O, центр C описывается как сфера с единичным радиусом, которая пересекает как конус C, так и C2 параллельно CX. РНС. 232. В CrC2 с общим полюсом d2 буква zt обозначает пересечение сферы и оси OdR, а точка r, где вращающаяся ось Oz пересекает сферу, характеризуется значением and. It всегда окружена 2 параллельными линиями, представляющими собой кривую от одной стороны к другой.

Если эти 2 параллельные линии находятся очень близко друг к другу, то ось тела рисует приблизительно конус вокруг оси Oz2.Для начальных условий, когда обе параллели совпадают ut = u2, ось Oz представляет собой ось Odr и точно конус, и в целом кривая, представленная точкой g, касается обеих окружностей C и C2.In фактически, мы используем дугу ztz = 6 и Полюсный угол xlztz = x , образованный дугой q, q и меридианом r1×1, чтобы определить положение точки q на сфере. Этот угол измеряется дугой xtn большой окружности с полюсом Dp.

Линия, образующая ось Ox и угол 01.Is перпендикулярно плоскости zfiz, поэтому дуга nl равна y X = Ф—у 53 С ду П П и ДТ ви w t dt 1 и Тогда, за исключением dt Д — Г iroa РСР 54. Это кривое дифференциальное уравнение, представляющее геометрическое положение точки z. из этого уравнения мы используем 1 квадратуру, чтобы получить y в функции и, следовательно, y в функции 9. Угол V, который образует касательную к геометрическому положению точки r с дугой ztz Меридиана, 1е,, = а Виден непосредственно из кривой прямоугольника, образованного крохотной дугой Треугольник ЗМЗ, ЗЗ. Ковчег пункт дуга Лели zm и Меридиан tg. в этом треугольнике угол z равен V. дуга mz равна d9,а дуга tg IA sin.

И это не удивительно, потому что радиус этой дуги это грех 9 рис. 232. cos 9 =и Ниже приведены Или на основе 54 ГПТ= 7 5 55 Угол V всегда является прямой линией. если u получает 1 или u из этих значений, f a будет равно нулю. Кривые фактически касательны к обеим параллелям рис. 232, , и III .Исключение составляют лишь те случаи, когда одно из ограничений u, u и v2 делает недействительным числитель j3 bgo. Затем на соответствующей параллельной линии tgV исчезает, и кривая имеет точку возврата на этой параллельной линии рис.232, .Ниже мы покажем, что эта ситуация может возникнуть только в более высокой параллели C2.

Например, если в пустоте брошена бомба и она в некоторый момент времени взрывается, то центр тяжести осколков будет продолжать описывать ту же самую параболу, так как силы, возникающие при взрыве, являются внутренними. Людмила Фирмаль

Чтобы увидеть, какую форму принимает эта кривая, рассмотрим направление, в котором радиус вектор дуги ztz может вращаться на сфере. Исходя из соотношения ды ты Г Бру ДТ ДТ у ды 8 Если значение равно, то значение будет содержать тот же знак. Числители не заключены между ними и ig. Тогда дуга ztz будет всегда вращаться в одном и том же направлении, а кривая будет иметь вид рис.232. если я Между и И еще i2.It может быть как положительным, так и отрицательным, и дуга z, z будет вращаться в одну или другую сторону. Кривая это привет Рис. 232. если дя равна 1 лимита, знак снова сохраняется, но кривая имеет точку возврата на параллельной линии, соответствующей этому пределу рис. 232, второй.

Эти 3 случая отличаются легкими начальными условиями. Если абсолютное значение больше 1, оно не может находиться между o и u2.Если абсолютное значение величины меньше 1, то выражение Он имеет тот же знак, что и a , который получается после замены этой суммы на f u .В зависимости от того, станет ли это 8 Если резидент положительный или отрицательный, то значение в первом случае заключено. между границами u1 и Uj, а если 2 я не между them. In в среднем случае значение a может быть равно нулю.

Тогда, или равный 1 из U2 limit. It легко увидеть, что это всегда Uj. In факт, давайте Затем, если вы замените f a на это значение, оно будет выглядеть следующим образом: Мшш и 1 из маршрутов между 1 и 1 ясен. Другой должен отключить выражение в квадрате brackets. As а результат и станет положительным, а значит Больше. Таким образом, поскольку только больший корень из and2 может иметь значение, Точка возврата может существовать только на верхней параллели C2.Этот последний случай имеет место при легко выполнимых начальных условиях, описанных в следующем разделе.

В случае формы III рис.232 рисунка на чертеже полное изменение, соответствующее периоду полных колебаний от ut до a2 и от U2 до uv, не равно нулю и имеет тот же знак, что и фундаментальное изменение этого угла в момент достижения u минимума uv точное доказательство этого свойства вы можете получить. Заметки Адамара H A d A m A g d, Bulletin des Sciences math M M M A M A M, 1895, f я часть, стр. 228. Бывают случаи, когда максимальный корень a2 будет равен 1.Затем верхняя параллельная линия вырождается в полюс R сферы.

Уравнение герполодии	Движение тяжелого твердого тела вокруг неподвижной точки
Интегралы, получаемые из общих теорем	Интегрирование в эллиптических функциях

Если вам потребуется заказать теоретическую механику вы всегда можете написать мне в whatsapp.