Случай квадратичной зависимости
Предположим, что между значениями фактора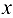 
и признака 
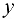существует квадратичная зависимость вида: 
.
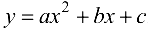Функция (24.2) в этом случае принимает вид:
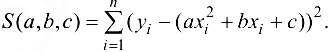
Это функция трех переменных: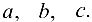 
Система уравнений (24.3) принимает вид:
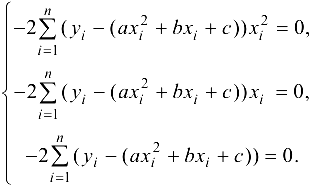
После преобразований, получаем
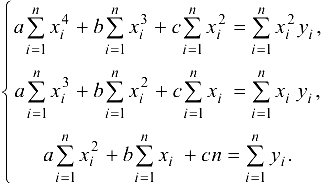
Получена система линейных уравнений для определения неизвестных 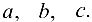Можно доказать, что определитель этой системы отличен от нуля, следовательно, она будет иметь единственное решение. При полученных значениях параметров функция 
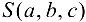будет иметь минимум.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
