Оглавление:
Случай, когда плоская система сил приводится к равнодействующей. Теорема Вариньона о моменте равнодействующей
Пусть некоторая система сил приводится к какому-то главному вектору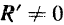 
, приложенному в произвольном центре 
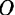приведения, и к какой-то паре с положительным моментом 
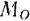(рис. 53,а).
Преобразуем пару с моментом 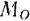так, чтобы силы, составляющие эту пару (обозначим их через 
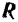и 
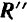), оказались равными по модулю силе 
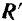. При этом нужно взять плечо 
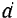этой пары таким, чтобы ее момент оставался равным 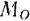. Тогда получим пару 
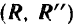, причем
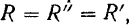
а плечо пары
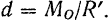
Воспользуемся тем, что пару как угодно можно переносить в ее плоскости. Перенесем пару 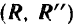так, чтобы ее сила 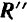оказалась приложенной в центре 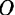приведения и направленной противоположно главному вектору 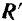(рис. 53,6). При этом направление вращения пары должно остаться неизменным (для 
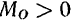оно должно быть противоположно направлению хода стрелки часов). Полученная плоская система сил эквивалентна силе 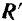и паре 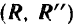. Но силы 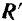и 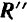взаимно уравновешиваются, а потому остается одна сила 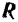, являющаяся, следовательно, равнодействующей этой системы сил.
Если система сил, при приведении к некоторому центру 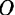, приводилась бы к главному вектору 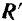и к паре с отрицательным моментом 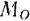, то, повторяя аналогичные рассуждения, мы также пришли к одной равнодействующей (рис. 53,в и г). Благодаря тому, что пара 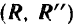имеет в этом случае противоположное направление вращения (по ходу стрелки часов), равнодействующая 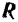окажется проходящей по другую сторону от центра 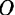приведения.
Как нетрудно видеть, в обоих случаях линия действия равнодействующей отстоит or центра 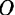приведения на расстоянии
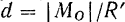
отложенном в такую сторону, чтобы знак момента равнодействующей относительно центра 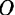приведения совпадал со знаком главного момента М0 (рис. 53).
Очевидно, если при приведении к какому-либо центру главный момент 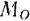системы сил относительно этого центра будет равен нулю, но главный вектор системы 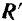будет отличен от нуля, то линия действия равнодействующей этой системы будет проходить через центр приведения.
Итак, если главный вектор данной плоской системы сил не равен нулю, то эта система приводится к равнодействующей, равной по модулю и направлению глав ному вектору.
При произвольном расположении сил на плоскости система может и не иметь равнодействующей, а приводится к паре. Но если только плоская система сил имеет равнодействующую, то эта равнодействующая во всех случаях равна по модулю и по направлению главному вектору 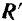. При этом для сходящихся сил линия действия равнодействующей проходит через общую точку пересечения линий действия сил. Для сил же, расположенных как угодно на плоскости, положение линии действия равнодействующей определяется величиной и знаком главного момента.
Как это видно из рис. 53,6 и г и из предыдущих рассуждений, модуль момент равнодействующей 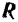относительно произвольно выбранной точки
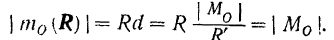
Знак же момента равнодействующей 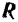относительно точки 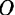также всегда совпадает (как это видно из сравнения рис. 53, о и б и рис. 53,с и г) со знаком главного момента 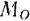. Но главный момент 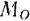данной плоской системы сил относительно произвольно выбранного центра 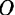приведения согласно (23) равен сумме алгебраических величин моментов составляющих сил относительно той же точки:
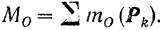
Отсюда следует:
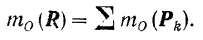
Момент равнодействующей плоской системы сил относительно любой точки, лежащей в плоскости действия данных сил, равен сумме алгебраических величин моментов составляющих сил относительно той же точки.
Мы доказали теорему, носящую имя французского ученого П. Вариньона (1654—1722), для случая плоской системы сил. Она справедлива и для произвольной пространственной системы сил. Только у для произвольной системы сил момент равнодействующей относительно любой точки равен геометрической сумме моментов составляющих сил относительно той же точки.
Пример задачи:
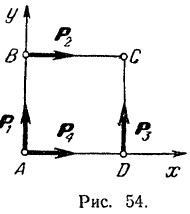
Вдоль сторон квадрата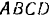 
(рис. 54) действуют силы, равные по модулю 
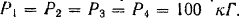. Сторона квадрата 
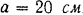. Привести эту систему к точке 
.
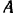Решение:
Проведем координатные оси так, как показано на рис. 54. Спроектируем на эти оси силы и определим их моменты относительно центра приведения. Найденные значения занесены в таблицу.
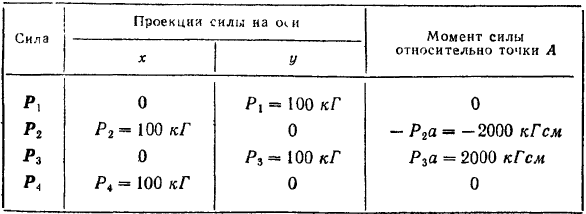
Проекции главного вектора
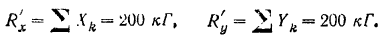
Модуль главного вектора
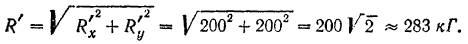
Направление главного вектора определится из формулы
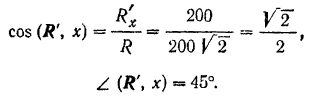
Главный момент относительно центра 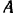приведения
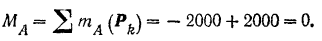
Так как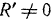 
, а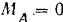 
, то система приводится к равнодействующей 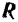, направленной по диагонали квадрата 
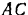и равной по модулю 283 кГ.
Тот же результат мы получили бы, если бы перенесли силы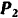 
и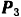 
в точку 
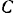пересечения их линий действия, а затем сложили бы по правилу параллелограмма эти силы и силы 
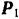и 
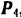приложенные в точке 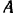. В результате мы получили бы две силы, направленные по одной прямой (диагонали квадрата 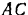) в одну сторону, которые можно заменить равнодействующей, равной по модулю
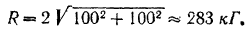
Пример задачи:
На мостовую ферму (рис. 55) действуют вертикальные силы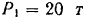 
и 
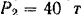, приложенные соответственно
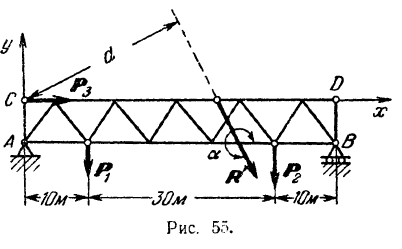
на расстоянии 10 м и 40 м от левого конца фермы, и горизонтальная сила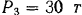 
, приложенная на уровне верхнего пояса фермы 
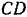. Высота фермы 6 м. Длина фермы 
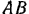равна 50 м. Определить равнодействующую сил 
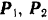и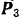 
.
Решение:
Примем точку 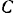за центр приведения. Для вычисления главного вектора и главного момента проведем координатные ос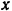и 
и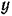 
(так, как показано на рис. 55), спроектируем все силы на эти оси и возьмем их моменты относительно принятого центра 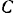приведения.
Проекции главного вектора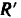 
на координатные оси равны
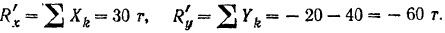
Отсюда находим модуль главного вектора
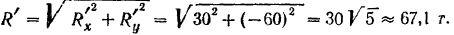
Так как главный вектор 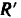не равен нулю, то система сил приводится к равнодействующей, равной по модулю и направлению главному вектору.
Направление равнодействующей определится из формулы:
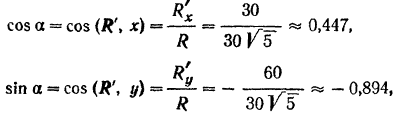
откуда
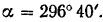
Линия действия равнодействующей проходит от центра приведения на расстоянии
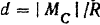
где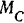 
— главный момент данной системы сил относительно центра 
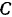приведения, равный
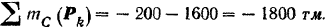
Знак момента показывает, что расстояние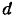 
должно быть отложено вправо от центра приведения (как показано на рис. 55).
В нашем случае расстояние
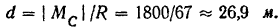
Зная расстояние 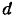и угол 
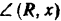, нетрудно при желании найти и точки пересечения линии действия равнодействующей с верхним и нижним поясами фермы.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
