Оглавление:
Случай, когда плоская система сил приводится к одной паре
Очевидно, что система приводится к паре, если ее главный вектор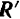 
равен нулю, а главный момент 
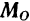не равен нулю.
Так как момент пары равен, как было доказано ранее (стр. 74), сумме алгебраических величин моментов составляющих ее сил относительно любой точки, лежащей в плоскости действия пары, то значение главного момента 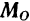в данном случае не может зависеть от выбора центра приведения. Иначе получилось бы, что одна и та же система сил заменяется парами с разными моментами, что невозможно.
Следовательно, если главный вектор плоской системы сил равен нулю, а ее главный момент не равен нулю, то эта система эквивалентна паре, момент которой равен сумме алгебраических величин моментов всех данных сил относительно любой точки плоскости.
Пример задачи:
Вдоль сторон квадрата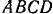 
действуют в одну сторону по их обходу равные по модулю силы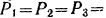 
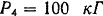(рис. 52). Сторона квадрата 
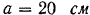. Привести эту систему к точке 
.
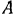Решение:
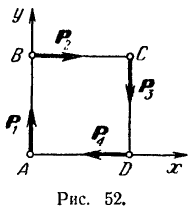
Проводим координатные оси так, как показано на рис. 52. Проектируем на эти оси все силы и определяем их моменты относительно центра приведения 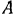. Найденные значения занесем в таблицу.
Проекции главного вектора: откуда главный
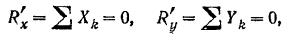
откуда главный вектор данной системы сил
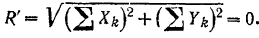
Главный момент этой системы сил относительно центра приведения
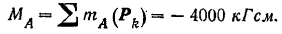
Так как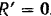 
, то система сил приводится к паре с моментом 
.
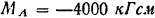К тому же результату можно было бы прийти и другим, более простым путем. Из рис. 52 видно, что заданная система сил состоит из двух пар: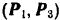 
и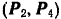 
, стремящихся повернуть квадрат по ходу стрелки часов. Но эти две пары, лежащие в одной плоскости, можно заменить одной результирующей парой 
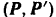. момент которой равен сумме алгебраических величин моментов составляющих пар
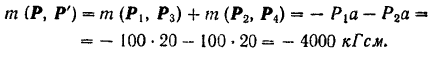
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
