Случай, когда плоская система сил находится в равновесии. Условия равновесия
Любая система сил эквивалентна по своему действию на твердое тело совокупности одной силы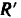 
, равной главному вектору этой системы, и одной пары, момент которой равен главному моменту 
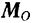системы относительно произвольно выбранного центра 
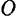приведения.
Следовательно, для равновесия системы сил, как угодно расположенных на плоскости, необходимо и достаточно, чтобы и главный вектор, и главный момент этой системы относительно произвольно выбранного центра приведения равнялись нулю:
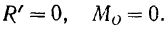
Из формул (8) и (24) для модуля главного вектора и главного момента плоской системы сил:
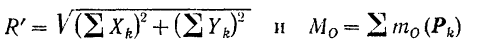
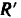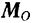следует, что и обращаются в нуль в том случае, когда имеют место уравнения
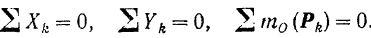
Для равновесия плоской системы как угодно расположенных сил необходимо и достаточно, чтобы порознь равнялись нулю сумма проекций всех сил на каждую из двух любых координатных’ осей, лежащих в плоскости действия сил, и сумма алгебраических величин моментов всех сил относительно любой точки той же плоскости.
Нужно заметить, что вовсе не обязательно каждую задачу решать при помощи двух уравнений проекций и одного уравнения моментов. Уравнения равновесия плоской системы сил могут быть выражены и в иной форме, а именно:
- Для равновесия системы сил, как угодно расположенных на плоскости, необходимо и достаточно, чтобы порознь равнялись нулю суммы алгебраических величин моментов всех сил относительно каждой из трех, произвольно выбранных, но не лежащих на одной прямой точек плоскости действия сил («Теорема о трех моментах») :
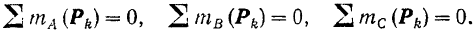
Необходимость этих уравнений следует из того, что при равновесии системы равна нулю сумма моментов всех ее сил относительно любой точки плоскости.
Достаточность же этих трех уравнений для утверждения о равновесии плоской системы сил вытекает из следующих соображений. Система не может приводиться к паре, так как в этом случае главный момент системы относительно любой точки плоскости равен моменту пары и не может равняться нулю.
При наличии данных уравнении система не может приводиться и к равнодействующей. По теореме Вариньона, момент равнодействующей относительно любой точки равен сумме моментов составляющих сил относительно той же точки и, следовательно, если бы равнодействующая существовала, то се линия действия должна была бы проходить через точк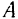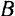и 
, 
и 
. Но они не лежат на одной прямой, и это невозможно.
- Для равновесия системы сил, как угодно располо-женных на плоскости, необходимо и достаточно, чтобы порознь равнялись нулю сумма проекций всех сил на одну какую-либо ось и суммы алгебраических величин моментов всех сил относительно двух любых точек плоскости, не лежащих на прямой перпендикулярной к выбранной оси проекций:
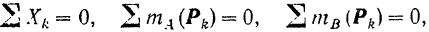
если ось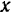 
не перпендикулярна к прямой 
.
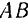Необходимость этих уравнений вытекает из того, что при равновесии системы равны нулю как сумма проекций всех сил на любую ось, так и суммы их моментов относительно любой точки. Достаточность же этих уравнений следует из того, что если бы равнодействующая существовала, то линия ее действия должна была бы проходить через точк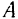и и 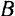. Но в этом случае проекция равнодействующей 
на ось 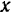, не перпендикулярную к прямой 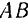, не может равняться нулю.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
