Оглавление:
Случаи сведения функций к линейной. Выбор «лучшей» функции
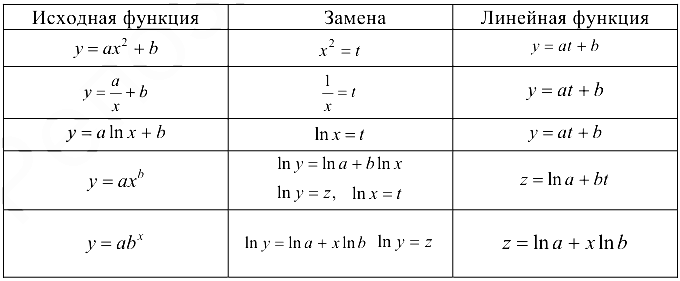
Рассмотрим другие виды функций, используемых в экономических исследованиях и способы их сведения к линейной зависимости, табл. 24.2.
Таблица 24.2
Для проверки адекватности построенной зависимости реальному поведению значений 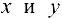 можно использовать коэффициент аппроксимации МАРЕ:
можно использовать коэффициент аппроксимации МАРЕ:
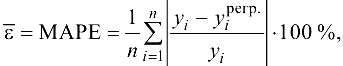
где 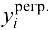 — значения функции регрессии, вычисленные по соответствующим значениям
— значения функции регрессии, вычисленные по соответствующим значениям 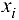 .
.
В случае, если 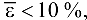 , полученная функция регрессии имеет высокую точность. Если
, полученная функция регрессии имеет высокую точность. Если 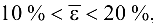 , точность функции регрессии хорошая (допустимая). При
, точность функции регрессии хорошая (допустимая). При 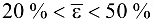 точность полученной функции удовлетворительная, однако использование данной зависимости па практике спорно. При
точность полученной функции удовлетворительная, однако использование данной зависимости па практике спорно. При 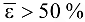 точность неудовлетворительная и использование данной функции в анализе недопустимо.
точность неудовлетворительная и использование данной функции в анализе недопустимо.
В случае если при исследованиях зависимость х и у определили с помощью нескольких функций, то для выбора «лучшей» рассчитывают среднюю квадратичную ошибку
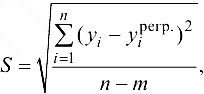
где 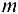 — количество параметров полученной функции.
— количество параметров полученной функции.
Для дальнейших исследований обычно используют функцию с наименьшей квадратичной ошибкой.
Пример 24.1.
В табл. 24.3 приведены данные о зависимости значений признака 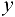 от значений фактора
от значений фактора 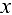 .
.
Таблица 24.3

Требуется:
1) построить функцию регрессии вида 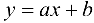 , оценить ее качество, найти среднюю квадратичную ошибку уравнения регрессии:
, оценить ее качество, найти среднюю квадратичную ошибку уравнения регрессии:
2) построить функцию регрессии вида 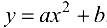 , оценить ее качество, найти среднюю квадратичную ошибку уравнения регрессии:
, оценить ее качество, найти среднюю квадратичную ошибку уравнения регрессии:
3) сравнить полученные результаты и сделать вывод о возможности их использования в прогнозировании.
Решение:
Для построения функций регрессии будем использовать метод наименьших квадратов. Все расчеты будем выполнять с точностью до трех знаков после запятой.
1. В случае линейной регрессии 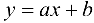 система для определения параметров
система для определения параметров 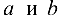 будет иметь вид (24.5).
будет иметь вид (24.5).
Все вспомогательные вычисления по определению постоянных коэффициентов данной системы представим в табл. 24.4.
Таблица 24.4
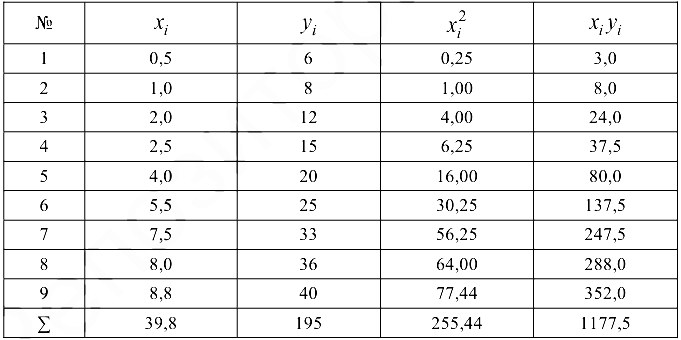
Система для определения параметров принимает вид:
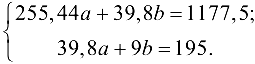
Воспользуемся формулами (24.6) и получим
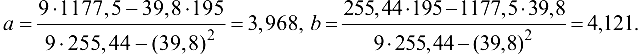
Таким образом, в случае линейной зависимости, функция регрессии принимает вид 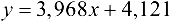 .
.
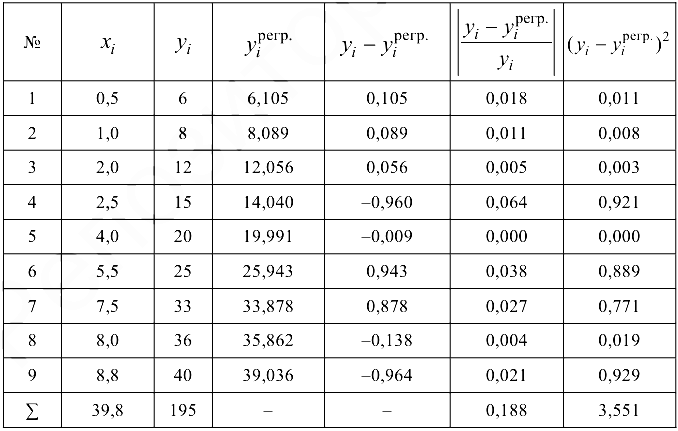
Для оценки качества полученной функции регрессии будем использовать коэффициент аппроксимации МАРЕ (24.7), среднюю квадратичную ошибку рассчитаем по формуле (24.8). Все вспомогательные вычисления представим в табл. 24.5. Согласно расчетам, коэффициент аппроксимации 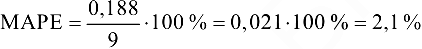 , что соответствует высокой точности функции.
, что соответствует высокой точности функции.
Средняя квадратичная ошибка составит 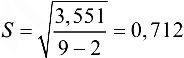 .
.
Таблица 24.5
2. В случае зависимости вида 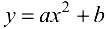 предварительно требуется выполнить замену
предварительно требуется выполнить замену 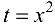 . Выполнив все вспомогательные вычисления по определению постоянных коэффициентов получим систему:
. Выполнив все вспомогательные вычисления по определению постоянных коэффициентов получим систему:
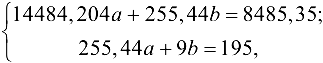
откуда 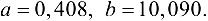 . Таким образом, в случае квадратичной зависимости, функция регрессии принимает вид
. Таким образом, в случае квадратичной зависимости, функция регрессии принимает вид 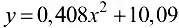 .
.
Кроме того, в данном случае вычисления позволяют получить следующие результаты:
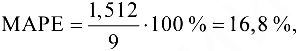
что соответствует допустимой точности функции регрессии; средняя квадратичная ошибка составит
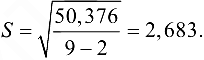
3. Таким образом, функция регрессии 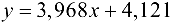 обладает высокой точностью, функция регрессии
обладает высокой точностью, функция регрессии 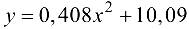 -допустимой точностью, а это означает, что использование первой функции обеспечит более достоверные результаты при прогнозировании. Средняя квадратичная ошибка для функции
-допустимой точностью, а это означает, что использование первой функции обеспечит более достоверные результаты при прогнозировании. Средняя квадратичная ошибка для функции 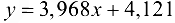 также меньше, чем для функции
также меньше, чем для функции 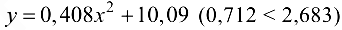
Вывод. На основе данных о зависимости значений признака 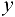 от значений фактора
от значений фактора 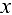 были построены две функции регрессии:
были построены две функции регрессии: 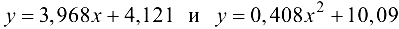 . В целях прогнозирования рекомендуется использовать зависимость вида
. В целях прогнозирования рекомендуется использовать зависимость вида 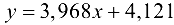 , так как опа обладает высокой точностью соответствия исходным данным и меньшей средней квадратичной ошибкой функции регрессии.
, так как опа обладает высокой точностью соответствия исходным данным и меньшей средней квадратичной ошибкой функции регрессии.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
| Случай линейной зависимости в математическом анализе |
| Случай квадратичной зависимости в математическом анализе |
| Элементы теории множеств: основные понятия |
| Логические символы в теории множеств |

