Оглавление:





Сложный и косой изгиб
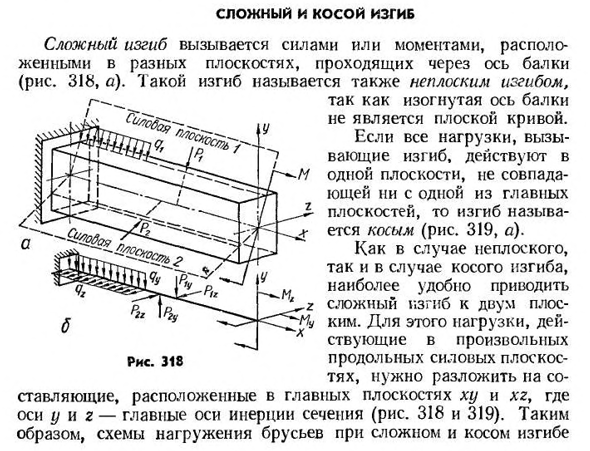
- Сложные и диагональные изгибы Сложный изгиб вызван силами или моментами, расположенными в разных плоскостях, проходящими через ось балки(рис. 318, а). Такой изгиб также называют неплоским изгибом, Триста восемнадцать риса Потому что криволинейная ось луча-это не плоская кривая. Если все нагрузки, вызывающие изгибающее действие в одной плоскости, не совпадают с одной из главных плоскостей, то изгиб называется косым (рис.). 319, А). Как для неплоского, так и для косого изгиба наиболее удобно свести
сложные изгибы к двум плоским изгибам. Для этого возьмем нагрузку, действующую на силовую плоскость в любом продольном направлении (318 и 319), которая разлагает компоненты, расположенные в главной плоскости XY и xz, где оси Y и g являются главными инерционными осями сечений. Поэтому механизм нагружения бруса при сложном и косом изгибе Рисунок
331могут представлен так, как показано на рисунке. 318 и 319, Б, Людмила Фирмаль
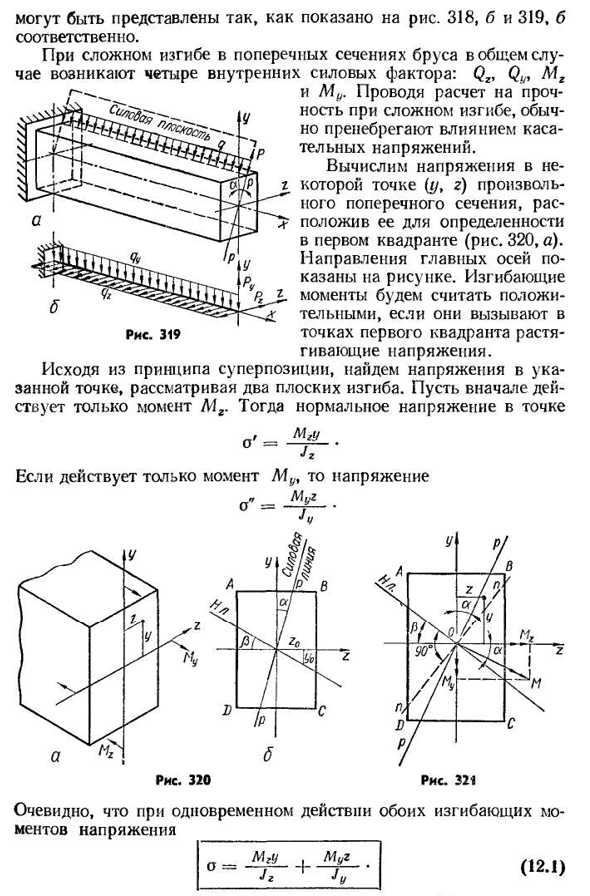
соответственно. При сложном изгибе в поперечном сечении балки, в общем случае, действуют четыре фактора внутренних сил: Qy, Mz и Mu. При расчете прочности сложного изгиба обычно игнорируется влияние касательного напряжения. Вычислите напряжение в определенной точке любого поперечного сечения (yt g) и надежно поместите его в первый квадрант(рис. 320, а). Направление главной оси показано на рисунке. Изгибающий момент считается
положительным, если он вызывает растягивающее напряжение в первом квадранте. Исходя из принципа суперпозиции, находим напряжение в указанной точке с учетом двух плоских изгибов. Пусть только тот момент, когда МГ будет действовать первым. И нормальное напряжение в точке Если действует только момент му, то напряжение Понятно, что при одновременном действии обоих
- режимов изгиба возникают напряжения (121) 332формула (12.1) позволяет определить нормальное натяжение в любой точке поперечного сечения при сложном, или, как еще говорят, пространственном, изгибе. Изгибающий момент и координаты точки, в которой определяется напряжение, подставляются в это выражение, используя их знак. Для косого изгиба(рис. 321) изгибающий момент L42 и Mu являются связанными зависимостями M2m cos OS; = m sin a, где M-изгибающий момент этого участка в силовой плоскости p-p(рис. 321). Тогда, используя формулу (12.1), это выглядит так МУ
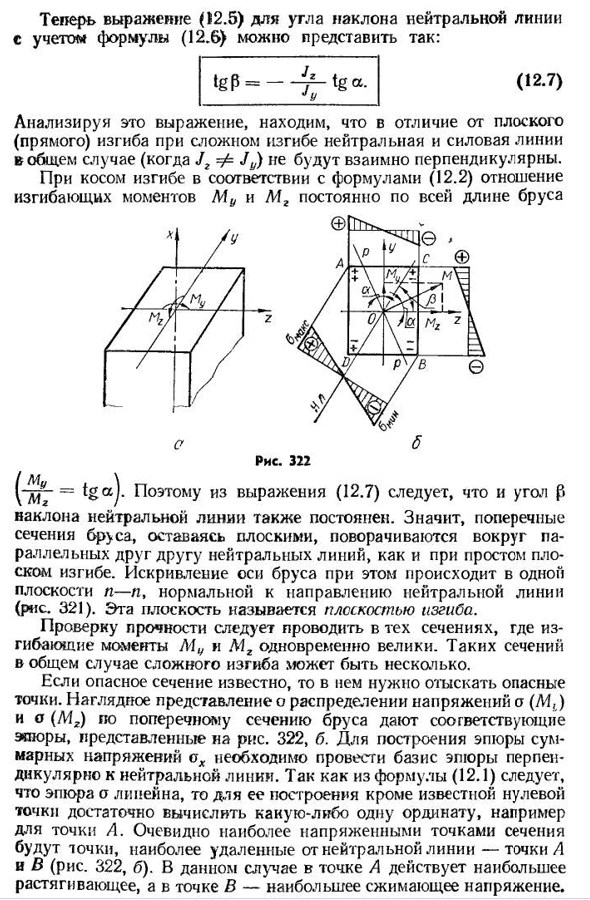
потому что. МЗ грех Но _ _ ———-)——— ———, Дж г * г Или O=m( — ± ^ — + • (12.3) формула для нейтральной линии в сложных изгибах в любом поперечном сечении выводится из Формулы (12.1), ставя О-О и через координаты точек нейтральной линии(рис. 320, б). Затем о= = 0. (12.4) это уравнение является уравнением прямой, проходящей через начало координат (центроидное сечение O). Расположение нейтральной линии характеризуется ее угловым коэффициентом В общем случае сложного (пространственного) изгиба угол наклона нейтральной линии вдоль оси балки является не постоянным, а M2 и Mu, который изменяется в зависимости от изменения отношения изгибающего момента.、 Если несколько участков балки, где изгибающий момент M2 и Mu(рис. 322, а),
необходимо найти положение нейтральной линии, полезно уточнить, чтобы указать Людмила Фирмаль
положение первой силовой линии р-р. проще всего это сделать 322, б) указывает направление результирующего вектора момента м, а следовательно, определяет уголг В частности, если прямоугольник ч_дя _ 2В-2В г * г в Таким образом, формулы(12.10) и (12.11)можно упростить следующим образом:. л (грех-ОВ-магистрали A1M х| Л уй Коза в У’ ЗГ / Раздел г= = Ж » Г г г Это полный бардак. Мин-A4max (12.12) В общем случае неплоского изгиба, условие прочности принимает вид (/Samake МУ, мг \ — Степень » + — ug — , по-видимому, существует такое же растягивающее напряжение по величине:°D-
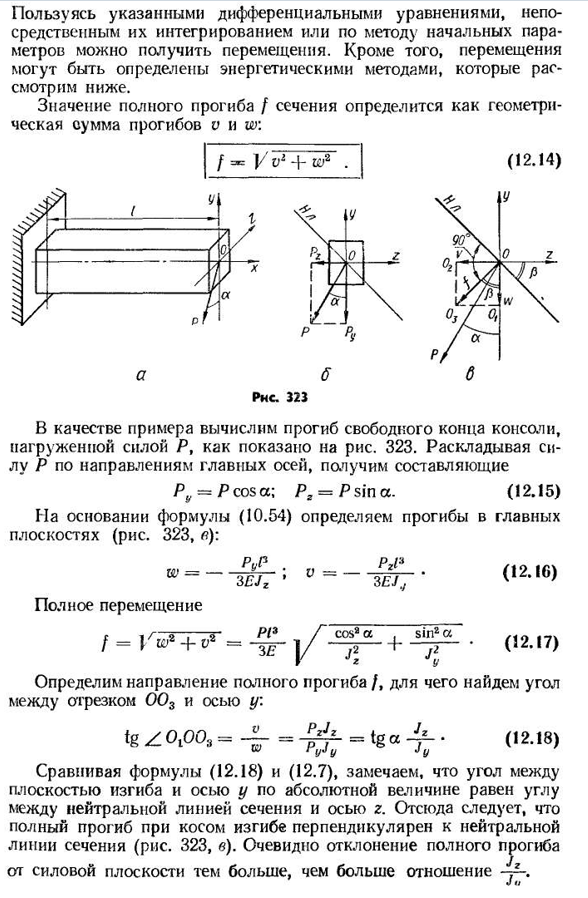
61″3kgf / cm2. Максимальное отклонение производится в середине пролета. Он определяется по формуле я ф л _ £ 381 за £ 7′ Она должна заменить ее компонент с направлением главной оси, а не сила распределенная нагрузка: ду-м соѕ а=400-0.894=357.6 кгс/м=3.576 кг, КЗ=г грех=400•0.447=178.8 кгс/м=1.788 кгс/м = 1.788 кг、 5^P_5^3,576-300″. Двенадцать. 381£7G384• 105 • 16 • 2 (M5^ 384^7^ ^
Смотрите также:
| Основы расчета балок на упругом основании | Изгиб с растяжением (сжатием) |
| Изгиб балок, материал которых не следует закону гука | Изгиб с кручением |

