Оглавление:



Сложение вращений вокруг пересекающихся осей
- Пусть тело участвует в двух вращениях одновременно: движение с угловой скоростью d и движение с угловой скоростью d2. Оси вращения пересекаются в точке O (рис. 95, а). Вектор угловой скорости как вектор движения можно считать переданным в точку О оси вращения. Примером объекта, ответственного за два поворота вокруг пересекающихся осей, является диск A, который свободно установлен на оси 00 и вращается с угловой скоростью 22. Наряду с осью 00 диск вращается вокруг другой оси OtOi (рисунок 95.6) с угловой скоростью Давайте определим тип движения твердого тела, участвующего в двух вращениях вокруг пересекающихся осей.
Точка O объекта на пересечении осей вращения фиксирована, и ее абсолютная скорость равна vo = 0. Вектор угловой скорости w>! Докажем другую точку M объекта на диагонали параллелограмма, построенного в. D2 также имеет скорость, равную нулю в момент возникновения проблемы. По теореме сложения скорости в точке M Рис. 95 Поскольку переносное и относительное движение — это вращение вокруг оси, 1’me = L1®, = 2пл. USD /; 1> мг = L2®2 = 2pl.D (? /? L /, Где d и d2 — кратчайшие расстояния от точки М до соответствующей оси вращения. Поскольку треугольники параллелограмма имеют одинаковую площадь, ome = smg.
В общем случае все шесть уравнений можно рассматривать вместе, так как правая часть этих уравнений зависит от шести параметров и их начальных производных, если сила зависит от скорости. Людмила Фирмаль
Векторы скорости yme и VMr находятся в противоположных направлениях. Следовательно, vMe = 0. Это верно для любой точки M на диагонали параллелограмма, поскольку векторную шкалу можно изменить. Скорость точки оси ОМ равна нулю. Таким образом, ОМ является мгновенной осью вращения тела в момент возникновения проблемы. То есть, если два поворота складываются вокруг пересекающейся оси, и одно является переносным, а другое — относительным, тело вращается вокруг мгновенной оси. Чтобы определить абсолютную угловую скорость вращения вокруг мгновенной оси, выберите точку W на теле, рассчитайте эту скорость как сложную скорость движения один раз, а другую — как вращение вокруг мгновенной оси.
- Согласно формуле Эйлера для вращательного движения со сложным движением, VN = VNe + VNr = aI XG + & 2XG = (®1 + II) XG. Для абсолютного вращения вокруг мгновенной оси я> N = кокср. Если скорость равна, ® = ®j + ®2, (3) Другими словами, абсолютная угловая скорость равна векторной сумме угловых скоростей вращения компонента. Последовательно применяя это дополнительное правило вращения вокруг пересекающейся оси, любое количество вращений вокруг пересекающейся оси можно заменить одним вращением, угловая скорость которого является вектором угловой скорости составляющих вращений.
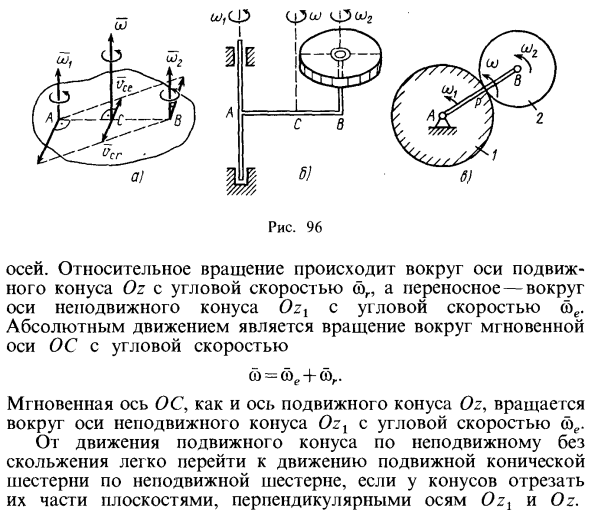
Равно сумме Тело, участвующее в двух вращениях вокруг пересекающихся осей, имеет фиксированную точку на пересечении осей. Вращается вокруг фиксированной точки. Другими словами, это перемещает сферу. Таким образом, движение сплошной сферы можно рассматривать как состоящее из двух поворотов (относительного и относительного) вокруг пересекающейся оси. Не катясь по неподвижному конусу 1, сфера движется во время катания с конусом 2 (рис. 95, в). Это движение можно рассматривать как две революции вокруг перекрестка Рис. 96 Ось.
Прежде чем рассматривать применение некоторой теоремы Карно, необходимо рассчитать кинетическую энергию потерянной скорости твердого тела, движущегося вокруг неподвижной оси или неподвижной точки. Людмила Фирмаль
Относительное вращение происходит вокруг оси подвижного конуса Oz с угловой скоростью <„, а удельное вращение происходит вокруг оси неподвижного конуса Ozt с угловой скоростью <ε. Абсолютным движением является ОС с угловой скоростью Вращение вокруг мгновенной оси. th = yue + th. Мгновенная ось ОС вращается вокруг оси неподвижного конуса Ozt с угловой скоростью, <аналогичной оси подвижного конуса Oz. Если конус отрезан частью с плоскостью, перпендикулярной осям Oz и Oz, перемещение подвижного конуса неподвижной шестерни будет менее скользким по сравнению с движением конической шестерни неподвижной шестерни.
Смотрите также:
Задачи по теоретической механике
| Сложение поступательных движений твердого тела | Сложение вращений вокруг параллельных осей |
| Сложение вращательных движений твердого тела | Пара вращений |
Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.

