Оглавление:














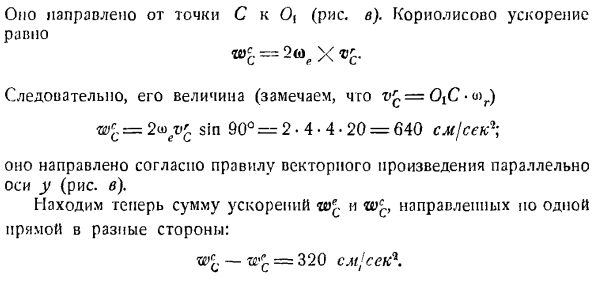

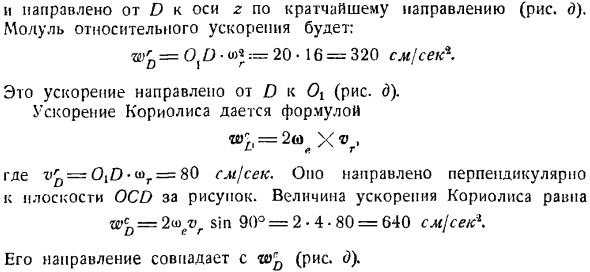



















Сложение вращений вокруг пересекающихся осей
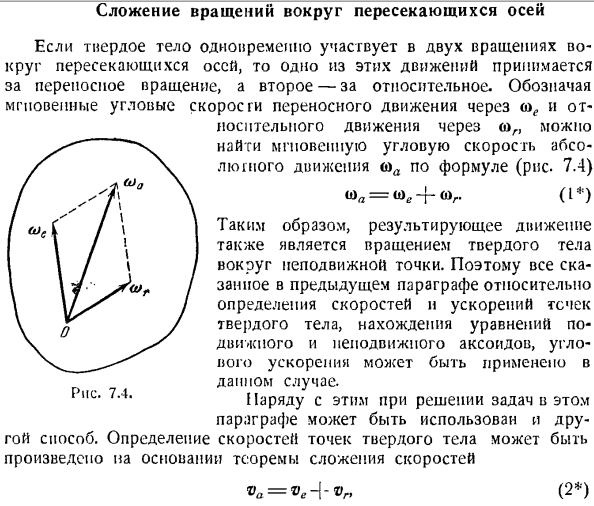
- Добавление поворотов вокруг пересекающихся осей Если твердое тело вращается 2 раза вокруг пересекающейся оси, то 1 из этих движений рассматривается как переносное вращение, а 2-как относительное вращение. мгновенная угловая скорость подвижного движения через ®01=®0、+®04 ′ Если считать равенство= 0, то оно выглядит так: Размер портативной скорости равен произведению радиуса поворота вокруг портативной мгновенной оси z и портативного модуля мгновенной угловой скорости.
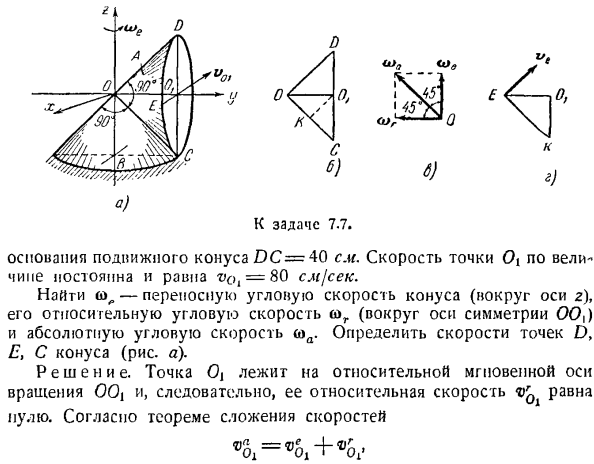
В * = 00 * О)、 -Я и есть ®0, _L0, — I 20-секунд Предполагая, что движение точки Oj происходит против часовой стрелки, вектор направлен вверх вдоль оси g при взгляде с положительного направления оси G. Конус а катится без скольжения вдоль конуса В, поэтому скорость точки подвижного конуса в контакте с поверхностью неподвижного конуса равна нулю.
Таким образом, шина ОС является мгновенной осью абсолютного движения, а абсолютная скорость точки о равна Людмила Фирмаль
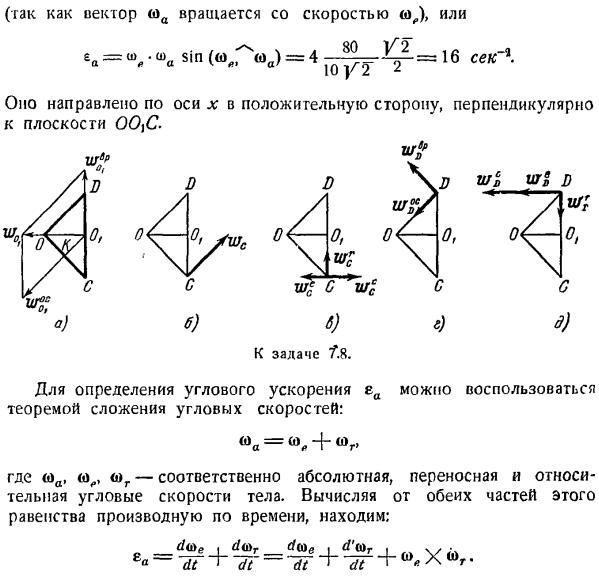
Где (а) — абсолютная мгновенная угловая скорость. 0 {K-перпендикуляр к мгновенной оси точки 0 {OS (рисунок O)).И затем… Олк = оол Син = 14,1 см Откуда? Следовательно、 ва 80 р. Учитывая направление скорости точки Ob, выполните с = < » * » г » г» Следовательно, величина u> r = w ^ = 4 сек ’\ Приступим к определению скорости точек D,£, C конуса. Скорость точки С равна нулю, поскольку точки эго находятся на мгновенной оси абсолютного движения и соприкасаются со сторонами неподвижного конуса В. Найти скорость точки D.
скорость точки D равна произведению следующей абсолютной угловой скорости. Кратчайшее расстояние точки D до мгновенной оси абсолютного движения ОС vd = OD•oa = = 20U2 = 160 см / с; < oD направлен перпендикулярно плоскости ODC (рисунок b) за пределами рисунка. Скорость точки D можно найти в другом way. In дело в том, что скорость точки D равна сумме переносной и относительной скоростей. = «£>+£>’Портативная скорость равна по размеру ^ = 00、-0、= 20-4 = 80 см! Считанные секунды.
- Каждый чертеж направлен перпендикулярно плоскости ОДК. Относительная скорость течки D vrD = Op•u> r = 20•4 = 80 с м / с. Потому что относительная скорость соответствует в том же направлении, что и портативная скорость、 v = v°D-j-vrD = 160 см / с Переходим к определению скорости точки E. d обозначает плоскость OjE / C, перпендикулярную абсолютной мгновенной оси OS, проходящей через диаметр o ^ E дна конуса. Из рисунка d видно, что кратчайшее расстояние от точки E до прямой линии OS равно ЕК = UV \ K)— \ -(еоху = / 200 + 400 = 24,5 см} поэтому скорость точки E будет равна: vF =ЕК -RR = 24.5 * 5.66 = 138.5 см / с
Задача 7.8.Определить абсолютное и относительное угловое ускорение конуса а в условиях предыдущей задачи. Найти точку Oi d, c ускорения. Решение. Угловое ускорение можно определить как скорость в конце вектора угловой скорости. Угловая скорость переносного движения O)^имеет значение= 4 сек ’ 1) и ее направление (вдоль оси z) остается неизменным.
Эта скорость (рисунок D) находится в плоскости О^ЕК и перпендикулярна линии ЕК. Людмила Фирмаль
Угол абсолютного ускорения движения 8 «==•»> <•。 0.) (точно так же, как вектор caa вращается со скоростью uJ, или V ^ a Sin K. *> a)= 4 10 лет, 2 года. Она направлена в положительном направлении вдоль оси Х и перпендикулярна плоскости 00] с. ш? Как определить угловое ускорение Теорема сложения ускорения: «= + Где<oa,<0 и <og-абсолютная угловая скорость тела, относительная угловая скорость и относительная угловая скорость соответственно. Если мы вычисляем производную по времени с обеих сторон этого уравнения, мы видим, что: — ДТ ^ ДТ-ДТ ^ ДТ Т ^ Х ^ ф 16 секунд.
d d ’ так как эта задача — ^ = 0 и — ^ = 0 Так… ea = X V V Если вы вычислите формулу напрямую, вы получите тот же результат из(1 ЕА = Х » = Х (<«,+(ОИ)=(1)е х » в Откуда? 16 секунд\ Определить ускорение точки Oit Dy C. ускорение точки Oi можно определить 3 способами. Первый способ-точка Oj, описывающая окружность с радиусом R> o1 = 80 см /с, постоянная скорость 004.Для этого Ускорение в точке 0{в модуле будет нормальное ускорение 1)’} — YaP2 = ^ = ^ = 320 см \ сек \ Он направлен от точки О к точке О. 2.
второй способ-ускорение эструса O, который принадлежит твердому телу, которое вращается вокруг неподвижного Сегура O. ®®,=®®,-г «ЗД=«аXКXГ)+е, XГ, кроме того, критическая величина бокового ускорения 2-o ^ • = V «2 −10-32 = 320 1/2 см}секунд*. Это ускорение перпендикулярно мгновенной оси, но перпендикулярно ей. O — K (рисунок a); модуль ускорения вращения wg> = tahi =£a * 00,= 16 * 20 = 320 см / с*、 она направлена перпендикулярно ha и r = 00, то есть к оси Z. обратите внимание на угол между w ^и 135、 w0i = 320 cmjsec *
И он направлен, но он соответствует результату, найденному в первом методе 00» 3-й метод-ускорение точки O, которое определяется теоремой сложения ускорений(теорема Кориолиса).И затем… Переносное ускорение направлено от O к O и имеет тот же размер, что и w * 0i = 00.•»о» = 20. 16 = 320 см / сек*; Относительное ускорение точки O равно нулю, поскольку точка O находится на оси OO и вызывает относительное движение конуса вокруг нее. Ускорение Кориолиса в точке O равно «O,= 2» X®r0l; Поскольку относительная скорость bj в точке O равна нулю, то disappears.
So, как и в ранее использованном методе, значение ускорения O выглядит следующим образом: w0i — = = 320 см С; это ускорение направлено от O к O. Найти ускорение точки C здесь. Это ускорение также может быть определено различными способами. Первый способ-ускорение в точке с состоит из вращательных ускорений, на которые не влияет ось Туалет = Ш ^ — Л Поскольку точка находится на мгновенной оси, то рьяное ускорение точки с устраняется. Для этого туалет = ш » Р = zaXr. Значение ускорения туалет = = ЕА * ОС * грех 90°: = 16. Заряд до 20 V2 = 320] / 2 секунды, и*.
Это ускорение находится в плоскости {OOXC} перпендикулярно к < ha>и образует прямой угол с ОС(рисунок B). 2-й метод определения ускорения точки с основан на теореме сложения ускорений. туалет = Вт:. — (- Душ ВКК Переносное ускорение точки C-это ускорение, когда угловая скорость вращается вокруг оси Z. wec = OS * sin 45° * u> j = 20 * 16 = 320 см / С1. Это ускорение направлено из точки с перпендикулярно оси z, то есть параллельно оси y(рис. Относительное ускорение в точке C — это ускорение, когда угловая скорость вращается вокруг оси Y.
Его значение wrc = OjC * co » = 20•1 b = 320 см / с Где v (, — абсолютная скорость точки, v (, и vr-ее переносная скорость и относительная скорость, respectively. To определить ускорение точки можно с помощью теоремы сложения ускорений (Korn-olis уа = у — \ — ут — \ — туалет>(3 *) Где wa-абсолютное ускорение точки. Вэй шя туалет-это соотношение рис-как, относительно, и Корниш ускорение, соответственно. Ускорение Коринолина определяется по формуле we = 2(0, x V V(4 *) Если вы решите проблему добавления поворотов вокруг пересекающихся осей, вы можете использовать 2 метода.
Первый способ. Из заданной угловой скорости переносного и относительного вращения определяется абсолютная угловая скорость, а кроме того, согласно установленной последовательности действий и§ 1 настоящей главы, определяются все искомые величины. Он направлен из точки C в 0 {(рисунок C).Ускорение Кориолиса равно ВЭС = 2 <о, Х ПТС Таким образом, его значение (v£= OtC•o) d) wrc = 2uv’c sin 90°= 2•4•4.20 = 640 cmIsec1.]
Он ориентирован по правилу векторных произведений параллельно оси y(рисунок c). Теперь найдем сумму ускорений wrc и wca, которые направлены в разные стороны вдоль 1 Прямой. Wc-wrc = 320 см / с * Тогда значение суммарного ускорения точки с wc = V (wrcf +(wcc-w7cY = 320 V 2 см / с; Он ориентирован под прямым углом к ОС. Определить ускорение точки D. Первый способ. Примените формулу распределения ускорения»} » к твердому телу, вращающемуся вокруг неподвижной точки. компания WD = накопители WD + WD с- Быстрое ускорение величины = OD■< « = 20/2 = 640 в » 2 см \ сек \ Он направлен от D К O(рисунок D).
Ускорение вращения определяется по формуле Поэтому модуль ускорения вращения =£a * OD = 1 (i * 20 V2 = 320 V 2 см / с— Это ускорение направлено перпендикулярно OD (рисунок D).Значение максимального ускорения в точке D компания WD = в(ВД?+ = 320U \ 0 см / с *. 2-й метод определения ускорения точки D основан на использовании теоремы Кориолиса. у> д = накопители WD + медиаплеер WD + WD с- Размер портативного ускорения такой же. ш * Д = ОД * грех 45° * у>
Причем он направлен от оси D к оси z в самом коротком направлении(рис. Модуль относительного ускорения является: wrD = O, O * 20 * 16 = 320 см / с*. Это ускорение направлено от D К 0 {(рисунок E).Ускорение Кориолиса задается формулой wr0 = х Где = OiO * ti> r = 80 см / с. За пределами фигуры она направлена перпендикулярно плоскости ОКР. Величина кориолисова ускорения равна wcD = 2u> vr sin 90°= 2.4.80 = 640 см / сек / с \
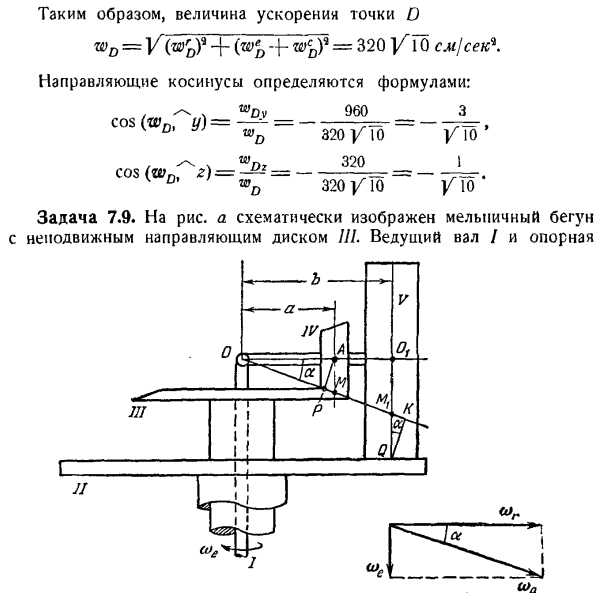
Его направление совпадает с направлением wrD (рисунок 0). Следовательно, значение ускорения точки O wD = + + = 320 / Go см / сек*. Направляющий Косинус определяется по формуле. В 960. Дифференциальный клапан потому что(БВ, г)= — — — =- Го ’ 1 320 Y. 320/20 д. потому что(БВ,=- 10. д. Задача 7.9.Рисунок мил-бегун с неподвижным направляющим диском III показан схематично. Приводной вал / и опора один.) К задаче 7.9. Пластины II могут вращаться вокруг вертикальной оси независимо друг от друга.
Вал 00 бегунка V имеет коническое место радиуса R, IV, твердо зафиксированное и свертывает без сползать неподвижный диск III радиуса A. Определите относительную угловую скорость u> r вращения относительно оси 00% бегунка и требуемую угловую скорость u> q для опорной плиты. Длина вала 00 ^равна радиусу B бегунка R. колесо IV обегает неподвижный диск за 4 секунды. Решение.
Движение бегуна является сложным, и вращение оси бегуна 00{вокруг вертикальной оси через точку O, а также вокруг собственной оси бегуна 00{первое из этих движений-вращение в вертикальном направлении-считается переносным Да.) Движение, а 2-е-вращение вокруг оси симметрии бегуна-относительное движение. Угловая скорость вращения бегунка портативного Го 71.、 <«П = Т = 2 1 < сек ’.Скорость центра а конического колеса IV равна ®А= ? В * г р ’.
Предполагая скорость точки А в положении, показанном на рисунке А, а, перпендикулярном чертежу, и равенство векторов к считывателю 0) (1 = 0) е-j-0) г Есть грабли, которые показаны на рисунке. а. это… .. 、 «V = w.> Ctg a = o) q cos x (1) при подстановке тригонометрических значений、 один. (О-о) — — — г * г 1г * Такая же угловая скорость вокруг OSP 00 имеет Бегун V. It является 1 твердым телом с коническим колесом IV. значение средней скорости o] бегунка V равно: Минимальная точка скорости Q бегуна может быть найдена двумя способами. Первый способ.
Рассмотрим бегун с абсолютным вращением вокруг мгновенной оси (ом).Продолжайте эту ось до точки пересечения с радиусом OtQ. Из треугольника сходства ГАМИЛЬЯМ и Оотми: Но… г о * Откуда? Тогда мы найдем тебя: Кук = 0, г-0,/ З= Р-РЛ. Минимальное расстояние точки Q от мгновенной оси вращения выглядит следующим образом: QK-QM, cos Z. = ^ ^ И затем… 2-й способ. Скорость точки Q бегуна представляет собой сумму переносной скорости вращения вокруг вертикальной оси бегуна и относительной скорости вращения вокруг его горизонтальной оси.
Обе эти скорости положений, показанных на рисунке, перпендикулярны плоскости чертежа, но направлены в разные стороны. Транспортная скорость ve направлена к нам, относительная скорость-от нас, vr ^> ve. Скорость эструса Q выглядит следующим образом. * (АР Скорость точки соприкосновения с бегунком на опорной плите 1J одинакова: vu = vg. Отсюда мы вычисляем значение угловой скорости Åpa- Пластина Пластина: Направление вращения пластины является противоположным направлению вращения вала бегунка. Задача 7-10.
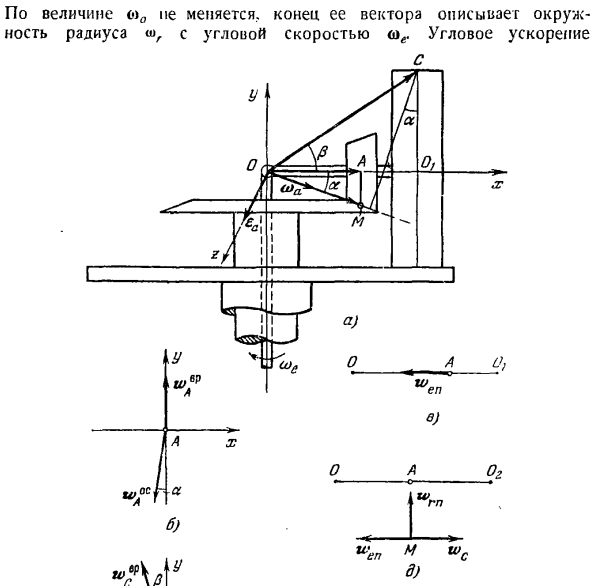
In по условиям предыдущего задания найдите точки ускорения A и L1 на коническом колесе и верхнюю точку C на бегуне. Решение. Во-первых, определить абсолютное угловое ускорение бегуна как производную от абсолютной угловой скорости по времени (ИЖ Размер (la не изменяется, и конец этого вектора представляет собой окружность с радиусом до углового ускорения при угловой скорости И 2-й способ. Рекомендуется следующая последовательность действий: 1) неподвижная система координат выбирается так, чтобы ось z совпадала с переносной угловой скоростью o)^,
а подвижная система координат выбирается так, чтобы ось z \совпадала с относительной угловой скоростью 0)^. 2) известной переносимой и относительной угловой скоростью является абсолютная угловая скорость. 3) определяются относительное и относительное отношение требуемой скорости вращения точки На фиг и, кроме того, требуемой абсолютной скорости.
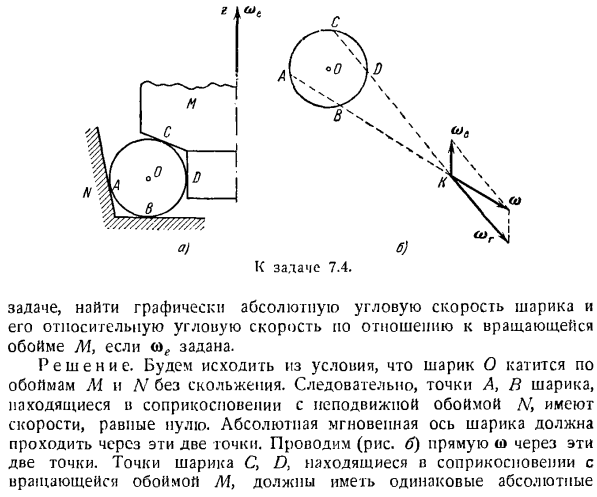
4) сложение векторов или сложение с помощью проекционного метода находят искомое абсолютное ускорение переносного ускорения, относительное ускорение, ускорение Кориолиса и даже точку твердого тела. Задача 7.4.Шарикоподшипник (рисунок а) состоит из неподвижной обоймы D; внутренней обоймы M, которая вращается с угловой скоростью<0 ^вокруг вертикальной оси z, и Шарика O, зажатого между обоймами. Определите положение оси z, по которой шарик катится вдоль зажима M、
«С Венгом д.) СГ. 1С.、 gp. е.) Вопрос 7.10 в Согласно (I), его можно рассматривать как скорость движения головки вектора. Вектор е углового ускорения, перпендикулярный чертежу, направлен к считывателю и численно равен (рисунок а). Ко, ко У.) — 4 г. * Точечное ускорение можно найти двумя способами: как применить теорему соперника и как применить теорему Кориолиса. Первый метод (теорема соперника).Используйте формулу для определения ускорения точек A, M, C. А! = ТТ) ВР ^ РЦ: = gXr_i.0)ІІХ (г) tl XГ)、
Теперь вместо r последовательно заменяем радиус-векторы точек A, M, C. 1)для ускорения эструса а: ОВЗ = Гал +(ОП х (©»XОЛ»).Вектор r XOL направлен вертикально вверх, а абсолютные значения равны ЛЗН = Р. Вектор o> d X OL ориентирован параллельно оси z и равен по величине% * Ол * грех=%/, g_ * Г_ = аз. один. Вектор (ol X (wa XОЛ) ориентирован перпендикулярно a) по оси Z и (2-й фактор векторного произведения расположен вдоль оси Z) ниже (Рис. Аль Ла. __ Вт.°с = о.01. в * грех 90°= — е-в А1 г *. Лаэ Г 1
Проекция ускорения точки A на координатные оси выглядит следующим образом: wLx = — w°£x = — sin a = — (D ^ a; < я) Р * » • > * А5 Вт,= ВБ? — Вт.°З = ФСФ-потому что — — — — — — = 0 Ай Ав Ав А А Д Так, ускорение точки А направлено горизонтально вдоль оси Х влево, а абсолютные значения равны. УА == <о? А = — 4-. Обратите внимание, что точка а вращается вокруг вертикальной оси с постоянной угловой скоростью<«><, как и любая другая ось на оси 00, поэтому она имеет нормальное ускорение, равное=•o, направленное к оси вращения. Горизонтально налево. Естественно, такой же результат был получен и при применении теоремы соперника. 2)
для ускорения точки М: ВМ = Е Х ОМ + » Х (<«*Х ом)’ Век r X OWI горы направлен перпендикулярно линии ом вверх, величина равна = £. РЭ = + Р \ Вектор oua X OM равен нулю, потому что факторы находятся в одном направлении. Следовательно、 О. Таким образом, максимальное ускорение в точке M состоит из вращательного ускорения n, а величина равна ВМ = ±Вач ^ = $ Он ориентирован перпендикулярно от точки м до точки ом. 3)для ускорения точки C, есть: «С = Е Х± ОС * Х (*>Х ОС)- Vekgor 8 x ОС направляется на плоскость XY, перпендикулярную к ОС,
размер такой же. ’<0 «(1 И*? — £*ОС-Лоза+ Ф. Итак, этот вектор находится в плоскости xy и образует ось y и угол 3. Размер ускорения всасывания выглядит следующим образом: I „инход1 =“ й» Где h-длина конверта.1, опущенный из точки C к мгновенной оси OM、 ч = грех (+)) = Дж / ΦR! (грех ведь?+ потому что грех Это уравнение, значение функции угла a, полученное в предыдущей задаче и、 sin 3 = — D^, получаем значение устойчивого ускорения А! ш <т = — pYa2 + б-(Мб + ар). Сильное ускорение направлено перпендикулярно линии ом от точки С к мгновенной оси.
Сечение вектора wc показано на рисунке. d. To определим величину ускорения точки с, рассчитаем компоненты ускорения по осям x и Y. Что купить: расширением WCX = — ЖНК? грех $ — уасси грех= —— *-(в стиле rbar)= wCv = ш ^ потому что п-ш£С, что а = — — — — й-я?) =-、 Откуда? ^ с = VwCx〜Р wCv = ^ Вrw-л-4aRr б-ф АА-отражателем маршрутов RR1-Д — Ж-А Р \ 2-й способ. Рассмотрим движение бегуна, чтобы быть сложным и использовать его, чтобы найти ускорение точки C в теореме Кориолиса. Вт = туалетом,+ вэн 4-wrz-е кол-е доп. Коэффициент: для движения,
Движение центрировано на вертикальной оси, и для относительного движения, Движение центрировано на оси 00.Заметим, что для всех точек WEX и wr_ равны нулю, так как угловая скорость не изменяет ни величины, ни направления. 1)для ускорения точки А существуют: U> A = *> en + U> rn + *> c коэффициент нормального ускорения при движении-подобное движение направлено в сторону оси вращения. То есть он будет горизонтально левым
. Горячий= Поскольку точка А находится на оси относительного вращения, нормальное ускорение относительного движения равно нулю. Поскольку относительная скорость эструса А равна пуле, ускорение Кориолиса равно пуле. Поэтому абсолютное ускорение точки(рис.) 2) для ускорения точки М: * > m = * > ep’t * * > RN + переносная точка вращения M необычное ускорение технологию wcn = к-ЕА Затем его направляют на переносную ось вращения (см. Рисунок е).
Нормальное ускорение относительного вращения Внешт = ^ р-р = г Он направлен к оси относительного вращения (над рисунком).Ускорение Кориолиса направлено вправо и равно туалет.= ВР греха 90°= 20)^. г = 2• Разработайте условия ускорения для этих осей вдоль осей x и y, как показано на рисунке. сайт WMX = — Вэнь-Ф — туалет = * — а)?а + 2Vila = аед Операции = кол = 0)Я Г• Абсолютное ускорение точки равно = г «4 + ®» = ^ л ^ М1 ^ = в ^ М1 ^ 3)для ускорения точки C, есть: w = 4 — + необычное ускорение при переносном вращении Вэнь = у * — б Причем он направлен в сторону переносной оси вращения, то есть влево(рисунок е).Нормальное ускорение точки M при относительном вращении направлено от M к оси OOj относительного вращения, то есть вниз, и равно следующим значениям: Ускорение Кориолиса направлено влево и равно туалет = 2 <oevr греха 90°= 2 <о / Орр = 2-ой.
Если спроектировать составляющие абсолютного ускорения точки С по осям, то мы увидим, что: ар. в Вот черт. = — ЕР-ЖВЦ ™—НБ-2(1)2 Д2 Величина абсолютного ускорения в точке с И>? ———— С = В-и — с, СV = 7 * ’+ + 4fl2 /?ва + fl4 /?ля= = В «r4i * + * Абрар 4а * р * р * + a4f?。 Задача 7L1.In дифференциал автомобиля(рисунок а), вращение от оси электродвигателя 1 передается через конические шестерни 2 и Б.
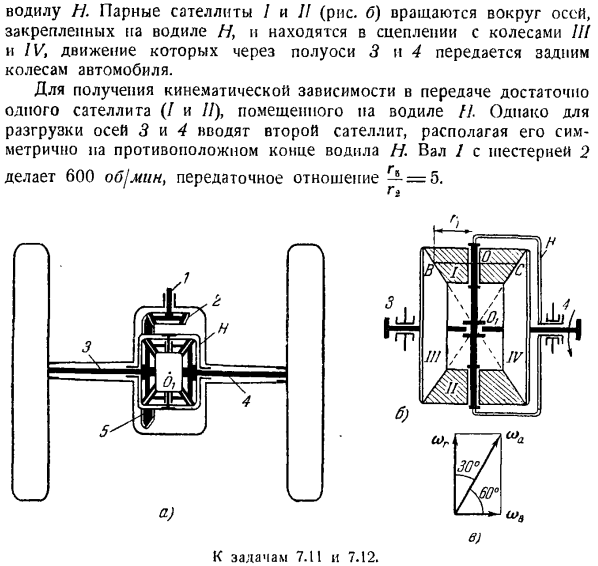
В Водитель N. сателлиты/и II пары (фиг.6) вращаются вокруг оси, установленной на водиле H, n входит в зацепление с колесами III и IV, а движение через оси 3 и 4 передается на задние колеса автомобиля. Для получения кинематической зависимости передачи достаточно 1 спутника (/и//), расположенного в драйвере II. Однако для разгрузки осей 3 и 4 вводится 2-й спутник, который расположен симметрично на противоположном конце несущей N. Будет 600 об / мин),
передаточное отношение^ — = 5. с.) / \ 3 _. Пункт меню \7.к. Употр. \ 4. \ один.) Задачи 7.11 и 7.12. если задано о, то задача графического нахождения абсолютной угловой скорости шара и его относительной угловой скорости относительно вращающейся клетки М. Решение. Исходят из состояния, когда шарик о катится, не скользя по обойме м и Ar. As в результате скорость точек A, B шара, контактирующего с неподвижным зажимом Nt, будет равна нулю.
Абсолютная мгновенная ось шара должна проходить через эти 2 точки. Нарисуйте (линия b) линию a) через эти 2 точки. Точка шарика C, D, контактирующая с вращающимся держателем M, должна иметь одинаковое абсолютное значение. Определите абсолютные и относительные угловые скорости спутника, а также угловые скорости передач / / / и IV. а) линейное движение автомобиля, Б) если правое заднее колесо останавливается при столкновении с препятствием.
Радиусы спутников I и II равны радиус g, = 15 см, шестерни III и IV-r3 = 15 | / » s cm. Решение. Указывает, что угловая скорость колеса 5 равна угловой скорости несущего устройства на 2.Далее, о парах конусов 2 и 6, это выглядит так: Откуда? = Q-120 об / мин. Зная угловую скорость носителя, метод Виллиса может быть применен для расчета угловой скорости звена дифференциального устройства автомобиля. Дай Мысленно основой механизма (рисунок Б)является вращение, противоположное вращению носителя, величина которого равна ему.
Тогда носитель не будет двигаться, а угловые скорости шестерен III и IV будут равны. И> 4-2. Угловая скорость спутника относительно носителя обозначается буквой О. затем можно описать уравнение для каждой пары колес с неподвижной осью. Далее, в Формуле (3) обмотка имеет знак минус, так как колеса III и IV (при остановке носителя) вращаются в противоположном направлении.
Решите уравнения (2) и (3) для 12 и h, и вы получите: (4) <、=£-(0)3-0,,)。 (5) Используйте эти формулы, чтобы найти ответ. а)при прямолинейном движении угловая скорость колес равна (jj3 = tu4, поэтому (4) имеет вид: (5) от: 0) 3 = 0,4 = 12 = 120 об / мин i o = 0 Спутник не вращается относительно несущей I. б) при остановке у правого заднего колеса автомобиля 3 = 1201/3 об / мин З. К.) Абсолютная угловая скорость спутника определяется из рис. c, где wr =(D = 120 1 ^ 3 об / мин,<0 ^ = 2 = 120 об / мин: ba = / / w * + Q, = 240 об / мин.
Задача 7. 12.Определить угловую скорость несущего колеса для дифференциала автомобиля, которая рассматривалась в предыдущей задаче、 Абсолютная угловая скорость спутника C равна радиусу задних колес автомобиля при вращении, рисуя дугу земли с радиусом Pj = 2 () м и p-2 = 18 м, а если скорость центра тяжести автомобиля равна^ = 38 м с. Радиус задних колес R = 0fi м. Решение.
Скорость движения центра задних колес автомобиля определяется по формуле В3 = С — J-С. = 40 м \ secKy в,= с — J-п= 3О м’sec. Пи’g’pl Р2 + Р3 Угловые скорости зубчатых колес III и IV (рисунок B) следующие: Вл в * — — — о>、— 3 R• ’ R• Затем из уравнения предыдущей задачи (4) находим угловую скорость носителя. о =(В3-я-со.)= 1 (В3-й-в()= Т = Т = 63.3 ы » г»、 Из Формулы(б) — относительная угловая скорость спутника г/ hП»1/3 фута?* — В4)»、
Для овладения навыками решения задач путем сложения поворотов вокруг пересекающихся осей, используйте И. В. Из»сборника задач теоретической механики» Мещерского, издание после 1950 года, рекомендуется решать следующие задачи:611、612、614、615、617、618 、622、627、630、632。
Поэтому относительная скорость утечки шарика при контакте с точкой зажима м равна zero. As в результате относительная мгновенная ось шара проходит через точку соприкосновения с вращающимся держателем m. проведем эту прямую линиюК. Грех Сири (Б-а)* Место, которое ты наконец нашел: Грех(5-а) (О =(1)—— Г и п sjh Задача 7.6.Искусственные спутники Земли, движущиеся по круговой орбите, имеют период вращения, рассчитанный по отношению к системе — * ) ’б) задача на 7.6.
Координаты, которые движутся с центром земли, в переводе эквивалентны 1,5 часам. Угол наклона орбиты относительно экватора aj = 60°определяет угловую скорость относительно Земли, которая вращается вокруг своей оси. Вектор его угловой скорости (SM) образует острый угол с осью Земли. Определение: плоскость орбиты K K образует экватор WO и угол 00°.Далее вектор ω абсолютной угловой скорости спутника образует осевой SM и угол 60°, вдоль которого направлен вектор угловой скорости Земли
. Если рассматривать вращение спутника как упражнение, состоящее из вращения, которое можно осуществлять вместе с Землей, и желаемого относительного вращения относительно Земли, то: Ш = <0£0)р、 Где ω-абсолютная угловая скорость спутника. co-относительная угловая скорость ее движения. Абсолютная угловая скорость −1. w = — min K переносное значение угловой скорости Итак, в треугольнике угловой скорости мы знаем 2 стороны w и угол между ними. Определите 3-ю сторону треугольника. р = » о? — 2М,
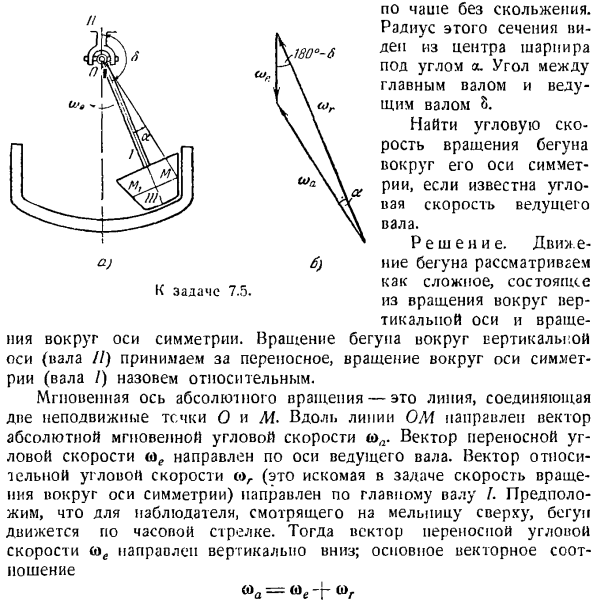
потому что В5 = 1-0 | /-1 -Ф〜. −1 ^ 0.0675 мин найти угол, образованный K-экватором и cur. потому что (и V-УО)= ^^ = 0.89 ft> r-угловая скорость спутника относительно Земли. Задача 7.7.Конус A, угол которого в вершине равен D0C = 90°, имеет неподвижную точку 0 и вращается без скольжения вдоль неподвижного конуса B. угол в Вершине также будет равен 90°.Диаметр U)
Смотрите также:
Предмет теоретическая механика

