Оглавление:




















Сложение вращений твердого тела вокруг параллельных осей
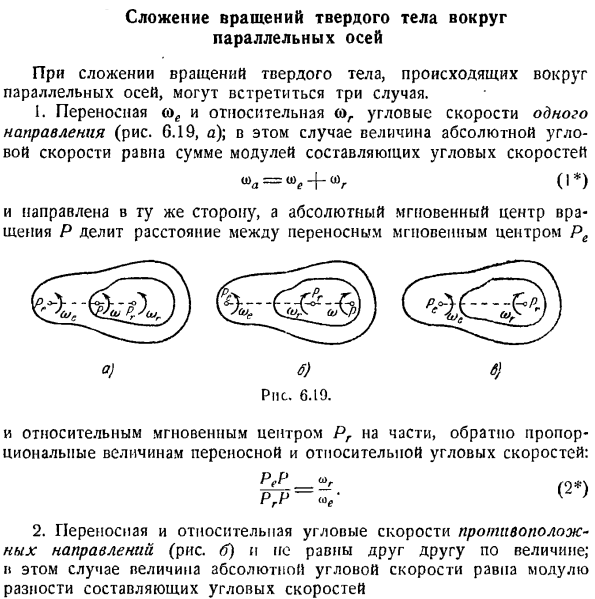
- Добавление вращения твердых тел вокруг параллельной оси Если добавить вращение твердого тела, которое происходит вокруг параллельной оси, может произойти 3 случая. 1.Переносной и относительной (однонаправленной) угловой скорости (рис. 6.19, а);в этом случае величина абсолютной угловой скорости равна сумме модулей составляющих угловой скорости) 0) =а(я), — ф0)р(я *) И абсолютный мгновенный центр вращения P, который направлен в том же направлении, делят расстояние между подвижным мгновенным мгновенным центром Pe.
о) Б) 6} Рис. 6.19. Относительный момент центра пр обратно пропорционален значениям полезной нагрузки и относительной угловой скорости. Не ^ г Прп — <ое’к] 2.Переносимость и относительная угловая скорость в противоположном направлении(рисунок B), но величина same. In в этом случае абсолютная угловая скорость равна абсолютному значению разности составляющих угловой скорости .
Потому что колеса II и 111 имеют одинаковую угловую скорость, а радиус отличается Людмила Фирмаль
Для колеса IV и V внутреннего блока шестерни, там: г. Равенство умножений (I)、(2)、(3)。Тогда, если колесо V не движется, а значит, равно o) о= 0、 З — & 2 г%г * ГЛ» г, г、 Если мы подставим значения всех величин в это уравнение, то увидим, что: Q, = 10000-1q, 46 =-1220 об / мин. Знак минус означает, что направление вращения кривошипа и первого колеса противоположной. в \ г (3) Да.) 5г
Задача 6.34.Вал газовой турбины dpigatel составит 25 ООО оборотов в минуту. Шестерня 1 с внутренним зубчатым колесом имеет зуб g = 120 и вращается вместе с валом I. шестерни 2 и 3, соединенные между собой, имеют 24 = 30 соответственно. И ha = 80 зубов. Они прикреплены к общей оси и вращаются с одинаковой угловой скоростью. Шестерня 3 зацеплена с колесом 4, соединенным с валом, на котором установлен гребной винт, что приводит к 1200 оборотам в минуту. Число зубьев в колесе 4^ 4 = 20.
- Определите угловую скорость, которая должна передаваться кривошипу, вращающему шестерни 2 и 3 осей. Решение: для решения этой задачи мы применяем метод Виллиса. / by / j, вал I и скорость стабильно Соединенного колеса 7, шестерня 2 и < 3 буки, а буква n ^обозначают угловой и неподвижно соединенный вал с пара-резьбой. Требуемая угловая скорость кривошипа, ИК один. 7. О. Я… } г / г; GTTG) г. 4. г.- В ’/ я И затем
К заданию 6.34. Угловая скорость Угол WOI / b Скорость колеса 4 черный воздух Ось, ведущая к вращению, на которой закреплены шестерни 2 и 3Y, называется n0.Приведем мысленно угловую скорость-70 / вращение к основанию механизма.
Затем кривошип останавливается, и угловая скорость колеса становится равной. Людмила Фирмаль
Колесо / колесо 2 и колесо 4 ПХ — / / 0, стр. 1-к, го -/ / 0 (1) Первая колесная пара во внутреннем зубчатом кольце имеет следующее: ИК — £2 Н ч0. Что касается 2-й колесной пары внешнего редуктора, то мы видим следующее: (3) Если умножить на равенство(2)и(3), то получится так: «1 -» о _ Я, — th0’g / Введение известного значения величины в это уравнение дает 1 неизвестное уравнение 25 ООО-па _ _ _ 30.20. 1200 ″ ~ ~ ~ 120•80 * ги-Ч О £ » / i4-квадрат Z. Откуда? «. = 23 600 об / мин
Задание 6.35.Носитель 5 вращается на вертикальной оси 00 с угловой скоростью 2.Перевозчик управляет песет на 2 вертикальных осей, из которых 1 является бесплатным для установки 3 шестерни/, 2, 3 бесплатно для того чтобы установить, и 1 является бесплатным для установки 4-мя передачами, а также. Шестерни 7, 2, 3 и 5 неподвижные Определите угловую скорость w, az3 передач/, 2, 3. Решение. Запишите формулу Уиллиса для каждой пары обязательств.
Для пары шестерен 5W 4: о)4-г _ г Где 4 и zK обозначают угловую скорость передачи и число зубьев сателлита 4 соответственно. К заданию 6.35. Размещены шестерни О Формула для Виллиса для оставшейся пары шестерен в сетке является: Пара 1-4 Для 3-4 пар И (2) 2 + 1 ′ Озеро. — В. Для 3-4 пар — ВОПРОС-(АЛЬ л> 4-г, г-I•ж
Каждое уравнение к экватору (1)(2)、(3)、(4) Если вы умножите его на, это выглядит так: И-Q _ Z В <о» — о_ з _ <1> 3-м з «—2-|- I ’- Q—T’ — Q 2 ^ 1 ′ Эти 3 уравнения определяют 3 угловых скорости, которые получены. Q О)= — О), −0; <03 =- 2 + 1 ′ * ’ J Z-I Так, шестерня 1 вращается в том же направлении, что и несущая, шестерня 2 постепенно перемещается, а шестерня 3 вращается в направлении, противоположном вращению несущей.
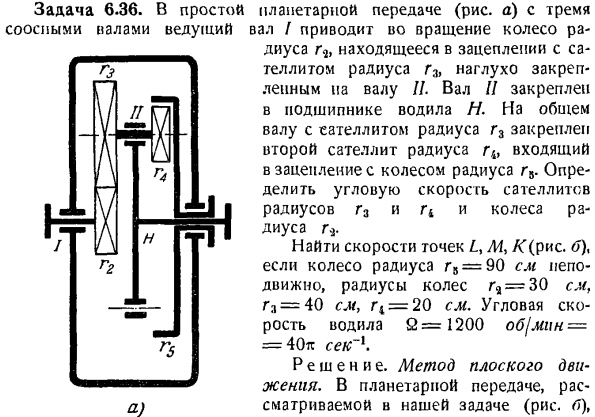
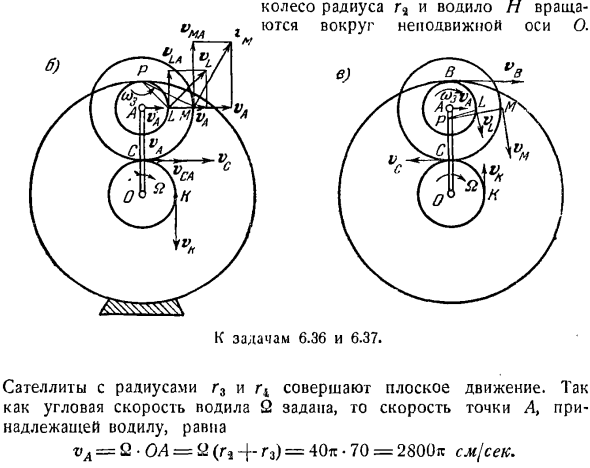
Задача 6.36. 3 простой планетарной передачи (рис) Вал/ведущее колесо радиуса r, которое входит в зацепление со спутником радиуса r3, прочно закреплено на валу R. вал/ / закреплен на водиле водила. Общий вал со спутником с радиусом g3 имеет 2-й спутник с фиксированным радиусом, который входит в зацепление с колесом с радиусом g5.Определить угловую скорость колес спутника и радиус R *радиус R3 и R4. Точка Z. найти скорость, М,/(’(рисунок B), радиус r5 = 90 см если колесо неподвижно, то радиус колеса равен r9 = 30 см, r3 = 40 sl, r4 = 20 s l /.Угловая скорость привода 2 = 1200 об / мин = = 40
Колеса радиуса m и несущей n вращаются вокруг неподвижной оси O. Перейдите к задачам 6.36 и 6.37. Спутники с радиусами r3 и r4 совершают планарное движение. С учетом угловой скорости носителя м, скорость точки А, принадлежащей перевозчику ва = 2•ОА = ч(г * + Г3) = 40tg-70 = 2800 * см / с / с Точка А является одновременно центром сателлитов радиусов r3 и r4 и совершает плоскостное движение.
Мгновенный центр скорости этих сателлитов, образующих твердое тело 1 (за счет того, что оба они прочно закреплены на валу), становится точкой контакта Р со спутником радиуса r4 и неподвижным колесом радиуса rv. Вы можете определить угловую скорость этого объекта В. В., 2800. * Х. Где AR-расстояние от точки A до мгновенного центра скорости.
Угловая скорость сои= i) 4, так что оба спутника движутся как одно тело. Определите скорость точки C, чтобы определить угловую скорость колеса в радиусе. Точка C является общей для сателлитов радиуса r3 и колес радиуса r9.Предполагая, что точка С находится на спутнике, определите скорость по формуле: ВК = <О3 * СР = «> с(Р3 + Р4) = 140 ^ −60 = 8400 ^ см / с Определите угловую скорость этого колеса, зная скорость точки С и думая, что она принадлежит колесу радиуса М. 3 SB g8 ^ 10 секунд•
Скорость точек L и M, принадлежащих спутнику, определяется по формуле: вл = iu3. Lp = 10gA Y 2 = 140 *. 20 U 2 = 3940kcm / s, vM = < 1) 3 * МР = о) 3 v r \ — \ — r \ = 140т:•44.7 = 6260 * CM / s、 LP и MP-это расстояние от соответствующей точки до мгновенного центра скорости. Так как точка K находится на колесе радиуса, которое вращается вокруг оси O с фиксированной угловой скоростью, то ее скорость равна ВК = з = 270i:-30 = 81 Отс см / сек Как и ожидалось, vK = vc. Метод Виллиса. Мысленно дайте вращение механизму с угловой скоростью −2 =-40 * С ’\
Когда несущая и неподвижна, угловая скорость всех колес уменьшается на эту величину, и зацепляющее колесо можно считать неподвижным осевым колесом. Для первой пары колес используем формулу Виллиса — М = Ха — £г’, При внешних зацеплениях колеса неподвижной оси вращаются в противоположном направлении, поэтому используется знак минус. Аналогично, для 2-й пары колес мы видим следующее: <> я-г _ > » г / Здесь используется знак плюс. Это связано с тем, что во внутренних зубчатых передачах оба колеса неподвижной оси вращаются в одном направлении.
Из последнего уравнения определите o> 4. −1200 _ _ _ 90# 1200 20 ′ Вот 5 = 0.Это происходит потому, что радиус rv колесо не движется из-за условий. Я найду тебя отсюда.: o> 4 = −4200 rImin = −140 G секунды Угловая скорость колеса с радиусом r3 такая же, как и у колеса с радиусом R4.Знак минус указывает на то, что вращение спутников g3 и ri происходит в направлении, противоположном вращению носителя. «„=И4 -“. Я 0. )
Максимальная составляющая угловой скорости (путь рис. 6.19, б) равна<>< и направлена к абсолютному мгновенному центру. Затем распределение P, расстояние между подвижной мгновенной скоростью PJ и относительной мгновенной скоростью PR, делится на внешнюю часть, обратно пропорциональную величине подвижной скорости и относительной угловой скорости: ПГ-Н -/^’ 3.At переносная относительная угловая скорость в противоположном направлении(рис. 0.19, в), размеры равны каждому other.
In в этом случае величина абсолютной угловой скорости пули равна, а твердое тело совершает поступательное движение、 Для определения скорости точек L и M используйте формулу распределения скорости и движения плоскости(рисунок а).Используйте точку полюса A, потому что скорость точки A известна по величине и направлению. Если предположить, что точки At и L движутся вместе с полюсами и вращаются относительно полюсов, то скорости в точках L и M будут следующими соответственно: = ’>Л + * Л>®Л1=■*> л + * мл> Куда? вла = ЮА. LA = Л Ч- Узнайте больше СВУ = »> с•С = О> С. Г3 = 140т:•40 = 5600t: см / cetcбыл.
Для точки C направление и < оСО совпадают、 ВК = ва + СВУ = 2800т: — Р oGOOt:= 8400t: см / сек. Для точки K, vK = vc-8400 м: см / с. задача 6.37.To решим предыдущую задачу, колеса радиуса rd соединены с двигателем, и если угловая скорость w8 = 3000 об / мин = 1007: сек, то эту передачу называют планетарной шестерней с двойным приводом или дифференциалом (рис. с). Решение. Метод плоскости movement. As показанный на рисунке корпус планетарной передачи двойного привода a, радиуса G. колесо 2, несущая Н, и колесо радиуса gv вращаются вокруг неподвижной оси O. сателлиты радиуса r3 и r4 совершают плоскостное движение. Поскольку задана угловая скорость 2, то скорость точки А, принадлежащей носителю, равна ва =вопрос: ОА = г (Р4 Р3)= 40т:•70 =
Определите расстояние AP от точки A до мгновенного центра скорости. Скорость движения точки в плоскости прямо пропорциональна расстоянию до мгновенного центра скорости. И затем… AR » или 2800l AR」 Vji _ АР + Г4 ijnrj 9000p_AR20 ’л’ Откуда? ЛР = 5 — = 9.05 см S Определить местоположение мгновенного центра скорости, зная величины скоростей vA и vD, можно по угловым скоростям спутников g3 и g4. Ва 2800 ^ 0, л.
Чтобы определить угловую скорость iOj, найдите скорость точки C, учитывая, что точка g принадлежит спутнику g3. У нас есть: Vc = 0) 3. Ср = <03 (Р3-АП)-9560 * cmIsec. Зная скорость точек C и r2, можно увидеть следующее: ио. Дж =!С = 9560Z = 319tc R2 с 30 Точки / принадлежащие спутнику. Скорость Ж определяется по формуле. VL = » a * g. r = 31 from: / g.; — f-АР1 = 31 отправление 22 = 6800 * CM / s、 ВМ = о> 4./ IR = 31 Otgu’R \ + AP * = 310 * * 41 = 12700 * см / с、 LP и / IR-расстояние от соответствующей точки до мгновенной скорости нейтрона. Скорость вк = Вк. Решение.
Метод Виллиса. Применяя формулу Виллиса к первой паре колес во внешней передаче, вы получите: Аналогично, для 2-й пары колес во внутреннем зубчатом кольце можно увидеть следующее: — Q-55 uj5-Q 44 * Из последнего равенства. ■О, −1200 90 3000-1200-20> Или 0> с = <= 9300 об / мин = 31 Он секунд Знак плюс указывает на то, что направление вращения спутника совпадает с направлением вращения носителя. Определение скоростей точек L и M, как указано выше, может осуществляться методом плоского движения.
При сравнении мы можем видеть, что метод Уиллиса проще, чем планарный метод. Для овладения навыком решения задач, добавляющих вращение вокруг параллельной оси, И. В. Мещерскому из сборника задач теоретической механики в изданиях с 1950 года рекомендуется решать следующие задачи:585、587、588、589、592、595 。 Точки выровнены перпендикулярно линиям равного RSRG, а модуль в = PcPr. АЭ = PcPr.<* Р. (о *) При решении задачи определения угловой скорости планетарных и дифференциальных передач обычно применяется формула Виллиса. Рис. 6.20.
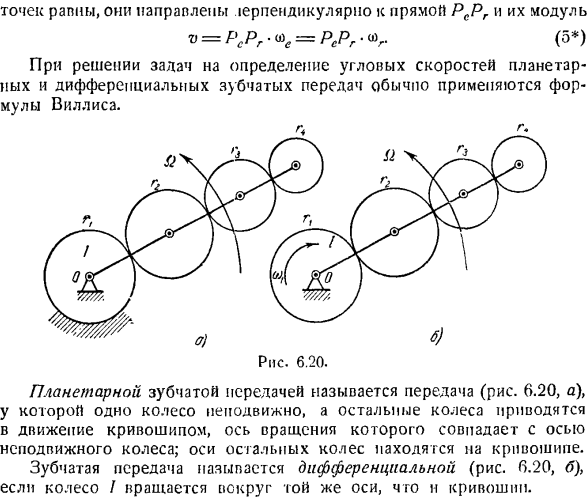
Планетарной зубчатой передачей называют передачу (рис.6.20,а), в которой 1 колесо неподвижно, остальные колеса приводятся в движение кривошипом, ось которого совпадает с осью неподвижного колеса. Ось остальных колес находится на кривошипе. Шестерня I называется дифференциальной, если колесо I вращается вокруг той же оси, что и кривошип (рис. 0.20, б). Да.) Рис. 6.21. Формула Виллиса определяет зависимость угловой скорости зубчатого колеса планетарной передачи от дифференциала в случае внешних и внутренних зубчатых колес.
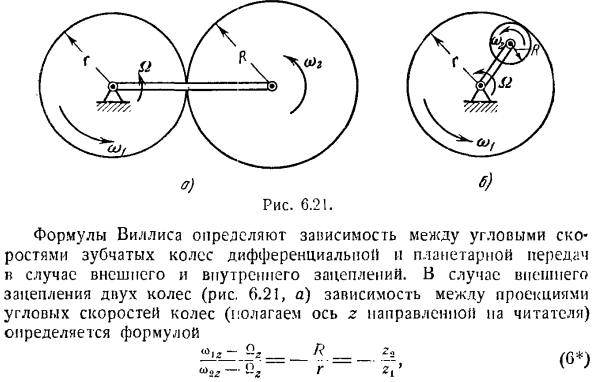
В случае внешнего зацепления 2 колес(рис. 6.21,а) зависимость между проекциями угловой скорости колес (при условии, что ось z направлена к считывателю) определяется по формуле: £3, ш? г. Где Ry g-радиус колеса, zh gg-число teeth. In внешняя и неподвижная ось, колеса вращаются в противоположном направлении, поэтому используется знак минус. Для внутренних шестерен на 2 колесах (рис. 6.12, б) эта зависимость имеет вид: — Qz_R / 7 * 4 Г> м-КЗ-г-в ’
Чтобы получить формулы(6 ) и(7), приведите в основу механизма вращение с угловой скоростью, направленной в противоположную сторону, при той же величине, что и угловая скорость кривошипа. После этого кривошип останавливается, и величина угловой скорости всех колес уменьшается. Затем вы можете учесть каждую пару зубчатых колес, которые вы зацепляете, и описать основные отношения между парой зубчатых колес, которые имеют фиксированную ось.
N метод Виллиса определяет абсолютную угловую скорость всех gears. In кроме того, можно найти скорость и ускорение любой точки звена механизма, используя формулы и методы определения скорости и ускорения точек тела при плоскопараллельном движении. Вы можете сделать что-нибудь еще. Во-первых, определить относительную угловую скорость и отношение угловой скорости, а затем использовать теорему сложения скорости и теорему Кориолиса, чтобы найти скорость и ускорение любой точки на колесе.
Такая последовательность действий рекомендуется при решении задачи сложения поворотов вокруг параллельных осей. А) в задаче па определение передаточного отношения, угловой скорости, скорости и ускорения различных точек планетарной передачи и дифференциала решалось методом планарного движения. 1) мысленно, к основанию механизма вращения с угловой скоростью, к угловой скорости кривошипа и к закону, дать рану в обратном направлении. 2) для каждой пары зубчатых колес создайте формулу (6) или (7),
которая представляет отношение между угловой скоростью зубчатого колеса. 3) умножьте все уравнения, составленные для каждой пары колес, чтобы определить угловую скорость крайней передачи. Значение угловой скорости промежуточного колеса (спутника) уменьшается, и определяется угловая скорость крайнего колеса. 4) определить положение центра момента, зная угловую скорость крайнего колеса и скорость его центра как точки, принадлежащей как колесу, так и кривошипу
6) определить предельное ускорение центра колеса как точки, принадлежащей кривошипу. 7) полюса экстремумов находят ускорение известной точки колеса по направлению, получают центр колеса, а затем находят угловое ускорение экстремума колеса, а затем находят ускорение любой из его точек. Б) задачи, определяющие относительную угловую скорость, подвижную угловую скорость, абсолютную угловую скорость, скорость и ускорение точки, которые могут быть решены с помощью теоремы сложения скоростей и теоремы кор и о л а.:
1) Выберите 1 поворот, если относительный, и 2-й поворот для результирующего перевода, если абсолютный. 2) однако по 2 известным угловым скоростям определяют 3-ю угловую скорость. 3) Используйте теорему сложения скоростей и найдите относительную скорость, переносную скорость или абсолютную скорость любой точки твердого тела. 4) Используйте теорему Кориолиса для определения относительного ускорения, переносимого ускорения или абсолютного ускорения любой точки в твердом теле.
Задача 6.32.Рассчитан период вращения искусственного спутника Земли, движущегося по круговой орбите, но относительно системы координат, которая постепенно движется вдоль центра Земли, он составляет 1,5 часа. Если орбита спутника совпадает с экваториальной плоскостью Земли, и спутник летит, то определяют угловую скорость относительно Земли, которая вращается вокруг своей оси. а)с востока на Запад, б) с запада на Восток. Решение. Земля вращается с запада на восток, за 24 часа она вращается 1
.Мы принимаем вращение Земли как подвижное movement. As в результате величина переносимой угловой скорости = = 24 Оффок. Установлена абсолютная угловая скорость спутника: 1 / с ’ Эта угловая скорость совпадает с направлением случая b)], соответствующей колесу/ 10 000 об / мин. Зная радиус колеса: g,= 10 см T ^ = 16 см, G 2 = 8 C My = 6 см、 Найти угловую скорость Q. It сначала необходимо доложить кривошипу, чтобы обеспечить требуемую угловую скорость на колесе. Решение.
Угловые скорости колес I, II, IV и V показаны в (•), o) i и w5 соответственно. Колеса//и один составляют 1 твердое тело и имеют общую угловую скорость * выберите ось z, которая идет к выноске, перпендикулярной плоскости чертежа. Опишите уравнение Виллиса для первой пары колес. Ши-КЗ __ р% » т * — КЗ Р ’ Аналогичными уравнениями формы колеса / / / и IV являются <°СЗ-з = р \ «щ-Р ’ Резьбовой стержень Направление Откуда?
Смотрите также:
Предмет теоретическая механика

