Сложение вращений тела вокруг двух осей
На рис. 11.1 изображено тело, которое совершает сложное движение -вращение вокруг оси, которая сама вращается вокруг другой, неподвижной оси. Естественно, первое вращение следует назвать относительным движением тела, второе — переносным, а соответствующие оси обозначить 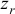 и
и 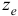 .
.
Абсолютным движением будет вращение вокруг точки пересечения осей 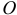 . (Если тело имеет больший размер, то его точка, совпадающая с
. (Если тело имеет больший размер, то его точка, совпадающая с 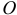 , все время будет неподвижной). Угловые скорости переносного вращения и относительного вращения изображаются векторами
, все время будет неподвижной). Угловые скорости переносного вращения и относительного вращения изображаются векторами 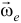 , и
, и 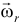 отложенными из неподвижной точки
отложенными из неподвижной точки 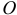 , точки пересечения осей, по соответствующим осям.
, точки пересечения осей, по соответствующим осям.
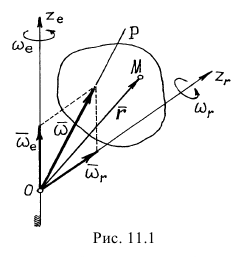
Найдем абсолютную скорость какой-нибудь точки 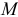 тела, положение которой определяется радиусом-вектором
тела, положение которой определяется радиусом-вектором 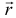 (рис 11.1).
(рис 11.1).
Как известно, она складывается из двух скоростей: относительной и переносной (10.5) 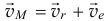 . Но относительное движение тела (используя правило остановки в разд.Х,§1) есть вращение с угловой скоростью
. Но относительное движение тела (используя правило остановки в разд.Х,§1) есть вращение с угловой скоростью 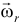 вокруг оси
вокруг оси 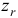 , а положение точки
, а положение точки 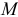 при этом определяется радиусом-вектором
при этом определяется радиусом-вектором 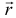 . Поэтому по (9.1)
. Поэтому по (9.1)
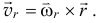
Переносное движение тела в данный момент времени, опять используя правило остановки, тоже есть вращение, но вокруг оси 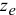 с угловой скоростью
с угловой скоростью 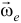 , и положение точки
, и положение точки 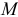 опять будет определяться тем же радиусом-вектором
опять будет определяться тем же радиусом-вектором 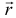 . Поэтому и переносная скорость
. Поэтому и переносная скорость
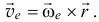
Абсолютная же скорость, скорость при вращении вокруг неподвижной точки 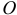 , при сферическом движении определяется аналогично (по формуле 9.3)
, при сферическом движении определяется аналогично (по формуле 9.3)
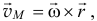
где 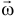 — абсолютная угловая скорость, направленная по мгновенной оси вращения
— абсолютная угловая скорость, направленная по мгновенной оси вращения 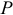 .
.
По формуле сложения скоростей получим
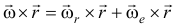
или
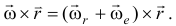
Отсюда
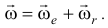
То есть мгновенная угловая скорость, угловая скорость абсолютного движения есть векторная сумма угловых скоростей переносного и относительного движений. А мгновенная ось вращения 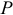 , направленная по вектору
, направленная по вектору 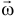 , совпадает с диагональю параллелограмма, построенного на векторах
, совпадает с диагональю параллелограмма, построенного на векторах 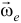 и
и 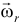 (см. рис 11.1).
(см. рис 11.1).
Частные случаи:
- Оси вращения
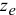 и
и 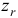 параллельны, направления вращений одинаковы (рис 11.2).
параллельны, направления вращений одинаковы (рис 11.2).
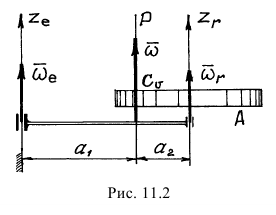
Так как векторы 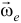 и
и 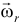 параллельны и направлены в одну сторону, то абсолютная угловая скорость по величине равна сумме их модулей
параллельны и направлены в одну сторону, то абсолютная угловая скорость по величине равна сумме их модулей
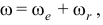
и вектор ее направлен в ту же сторону. Мгновенная ось вращения 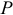 делит расстояние между осями на части, обратно пропорциональные
делит расстояние между осями на части, обратно пропорциональные 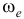 и
и 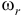 :
:
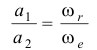
(аналогично равнодействующей параллельных сил).
В этом частном случае тело 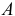 совершает плоскопараллельное движение. Мгновенный центр скоростей
совершает плоскопараллельное движение. Мгновенный центр скоростей 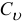 находится на оси
находится на оси 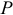 .
.
- Оси вращения параллельны, направления вращений противоположны (рис. 11.3).
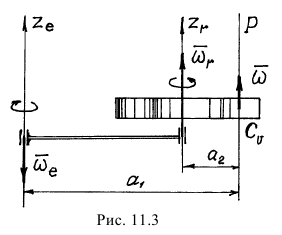
В этому случае 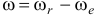 (при
(при 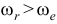 ). Мгновенная ось вращения и мгновенный центр скоростей находятся за вектором большей угловой скорости на расстояниях таких, что
). Мгновенная ось вращения и мгновенный центр скоростей находятся за вектором большей угловой скорости на расстояниях таких, что 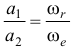 (опять по аналогии определения положения равнодействующей параллельных сил).
(опять по аналогии определения положения равнодействующей параллельных сил).
- Оси вращения параллельны, направления вращений противоположны и угловые скорости равны
Угловая скорость абсолютного движения будет равна нулю и, следовательно, тело совершает поступательное движение. Этот случай называется парой вращений по аналогии с парой сил.
Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:
Помощь по теоретической механике
Кстати возможно вам будут полезны эти страницы:
| Определение абсолютной скорости точки |
| Определение абсолютного ускорения точки |
| Аксиомы динамики в теоретической механике |
| Динамика материальной точки |

