Оглавление:







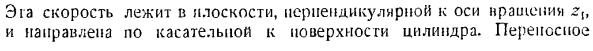
































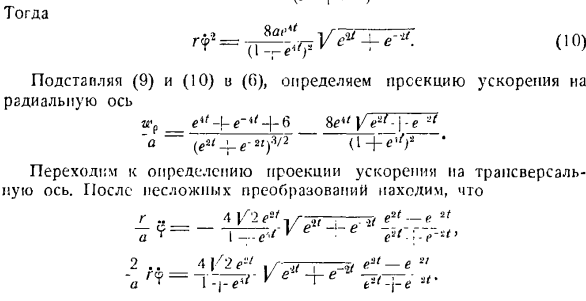


















Сложение ускорений
- Добавление ускорения 1 Определение точечного ускорения в переносном поступательном движении и произвольном переносном движении. Соотношение между абсолютным, относительным и точечным ускорениями в соотношении (рис.) движения определяется теоремой сложения ускорений, называемой Теоремой Кориолиса. Уа = У — \ — Ут — \ — Душ, Туалет. (1 )
Согласно этой теореме, we>относительного ускорения wr и кориолисова ускорения wr. Чтобы определить относительное ускорение точки, нужно мысленно отвлечь внимание от соотношения движения движения и вычислить относительное ускорение по правилам кинематики точки.
абсолютное ускорение точки wa равно геометрической сумме переносного ускорения Людмила Фирмаль
Чтобы определить переносное ускорение, мысленно остановить относительное движение точки и вычислить переносное ускорение по правилам кинематики точки Абсолютная скорость находится в «касательной плоскости цилиндра», которая создает шину и угол а цилиндра. ТГА ==?-£=== 5 ^^ 2-4.14 = 8.28。 (о) В качестве производной от относительных координат оси времени определите проекцию относительного ускорения оси Oxj, Oy\, Ozi. WRX, с = н «| =-12 * 1, потому что 2 * / =-4?Ари, а> р>.= п= — 12д.2 sin2n/ = — 4- \ ИБ «В,= = 0.Величина относительного ускорения равна Рэв = Г + Я + Я = 1; У.
Это ускорение ориентировано вдоль перпендикулярной линии, поднимающейся от точки М к оси вращения, поэтому оно совпадает в том же направлении, что и переносное ускорение(см. Рисунок).Ускорение Кориолиса равно туалет == х Величина кориолисова ускорения определяется по формуле Ух… туалет = 2 < * ЭВР грехе(о> т, ВР)= ’ 2И » ЭВР ху = 2Д)с•6Т: = 24tg м / ы / л Направление ускорения Кориолиса определяется правилами генерации векторов или П. Ф.. Он обнаруживается по одному из правил Zhukovsky.
- To при этом вектор относительной скорости проецируется на плоскость xv, а направление вращения задерживается вектором угловой транспортной скорости (Окружной), и эта проекция направлена в направлении вращения W6 в плоскости xy ОО0.Это будет направление Кориолиса acceleration.
As в результате кориолисово ускорение направляется вдоль перпендикулярной линии и поднимается от точки L1 к вращательному естественному по, Где направление совпадает с переносным и относительным ускорением. Поэтому величина абсолютного ускорения равна арифметической сумме отношения кориолисова относительного ускорения и кориолисова ускорения. да = мы-ГСГ-г у«,- = И2-Джей — 12tg- — й-24Т:^ 206.5 МС(( «) Он направлен от точки эструса L1 вдоль перпендикулярных линий, прикрепленных к оси вращения (см. Рисунок).
проекция относительной скорости на горизонтальную плоскость vrxy и скорость перемещения направлены вдоль 1 прямой, но в разных направлениях directions Людмила Фирмаль
Теперь рассмотрим случай=-2 sec1.In в этом случае, по сравнению с предыдущим, происходят только следующие изменения: . So, Формулы(4)и(5)принимают вид: * = В (vrxy-магнитофон- \ в * Р2 == 1 /(6 *-6)4ч-3 * ^ 13.2.я / с,(4 ’) тг.» = = = 2•2.14 = 4.28。 (5 ’)
Ускорение коллизии ориентировано вдоль перпендикуляра Yum, удерживая значение sysy, и направлено от точки M к оси вращения, но co направлено в противоположную сторону, потому что co направлено в противоположную сторону. Поэтому величина абсолютного ускорения одинакова. W = we-xs’L-wc = 1 2 12tg-24th-55.5 m’SEC. (6 ’)
В этой задаче ускорение переносного, относительного и кориолиссона было направлено вдоль 1 прямой, а определение абсолютного ускорения ограничивалось алгебраическим сложением этих величин. Заметим, что 3 составляющие суммарных ускорений указывают на то, что такое совпадение во всех направлениях нехарактерно. Непреодолимый. В большинстве случаев компоненты абсолютного ускорения направлены вдоль различных прямых, а их сложение осуществляется векторным способом.
Задача 5. 16.To для передачи поступательного движения машины используется механизм, состоящий из прямого стержня, который вращается с постоянной угловой скоростью / н V-d’I-sin — <или•1> Потому что точка А движется линейно. Величина ускорения в точке А определяется как производная от времени и скорости dv 2 / о> * coso»/ / Г1Ч 2-й способ. Рассмотрим абсолютное перемещение точки А ползунка как сложное: вращение с помощью переносного стержня ОА
Относительное линейное движение вдоль стержня ОА. Да, портативный модуль скорости для точки А выглядит так: V = OA•o)= -. е грех <Ф Скорость перехода ориентирована перпендикулярно к штанге OA, поэтому она формирует штангу и угол 90 градусов. Скорость мигания (хотя это линейное движение ОА) равна среднему ОА времени 01 и ориентирована вдоль ОА. Д Ф! \ _ _ , потому что » от Р ДТ СМЭВ \ <у / грех-Ч> Т ’
Векторная форма сигнала (рис. 6) в.-= ве — \ — ВР、 Определить абсолютную скорость движения точки А в направлении действия препарата. 。 | | /. / ’ .Я х V = — V. подоконник и/! — COSШ1— / Ш. И-Ф-Джей! =- e r \ 1 SUIJ t (1) чтобы соответствовать. Переходим к определению абсолютного ускорения точки А. согласно теореме сложения ускорений ш = у — \ — водонепроницаемые-туалет (3) поскольку к = const, то величина переносного ускорения выглядит так: Он направлен от A к центру O (рисунок C).
Значения Гнойного ускорения и прямолинейного движения составляют _dvr 1 <Ч1-Джей-потому что — у> г Водонепроницаемые ДТ ~~ ВСН? Он направлен на прямую линию ОА. Ускорение Кориолиса равно по величине «2 <ој / потому что Вт,= 2tot;, то Sin 90°= — г -. 1 р грех-у>£ Ускорение разгона определяется поворотом горы со скоростью 1 градус 90 градусов, как и в рассматриваемом случае, со скоростью 90 градусов. vr перпендикулярно к < o. далее при построении векторного уравнения (3) в направлении абсолютного ускорения, совпадающего с осью、 。 и… 。 。 , ’21 <Х — с COS <от W.-r-w.) COS w / — & & t = — счет \ ’с грехом „хит“ 4io такая же, как (2)
. Задача 5L7.На плоскости изображена дуга с радиусом r = 800 м по кривизне при постоянной скорости 160 м / ceic. Касательная к траектории движения самолета на ходу совпадает с продольной осью самолета. Поршень двигателя движется в направлении продольной оси по формуле x {=5 cos2 g/, а ось X] направлена к носу самолета. К задаче 5.17. Определите относительное, переносное, абсолютное и ускорение поршня в заданный момент времени /» = 0, ф | = 0.25 ЦСК/., = 0,5 сек.
Обратите внимание, что расстояние от поршня до центра круга не изменяется, предполагается, что оно равно 80(> m).Небольшие изменения в этом расстоянии из-за поршня игнорируются. Решение. Мы садимся в самолет для путешествия в салоне. Рассмотрим движение поршня относительно плоскости как относительное движение. Движение поршня относительно Земли состоит в движении, связанном с плоскостью и с плоскостью, которая является абсолютным движением поршня.
Полезная нагрузка поршня-это скорость той точки на плоскости, которой поршень в настоящее время соответствует. Портативный модуль скорости ve = 160 л / с Величина угловой скорости подвижного движения определяется по формуле в.. 160… CO = r = — = 0 1 ЦСК. Е Г <800 ′ Повторное ускорение поршня ускорение является ускорением точки плоскости, на которой поршень в настоящее время coincides. It он в пути
. Когда самолет движется с постоянной скоростью, переносное ускорение является обычным переносным ускорением, и его значение v \ 1602,2 = wen = = 32 м \ сек \ Это ускорение направлено к центру круга, который рисует плоскость. Определить положение летательного аппарата в момент времени / 0, т. к. самолет вращается с постоянной угловой скоростью»>,, =угол поворота прямой, соединяющей центр прямой вокруг центра прямой и при этом плоскость является <п = » > Эт、
Также соответствующий момент (угол измеряется в радианах) — f0 = 0, cf,= 0.2•0.25 = 0.05.?= 0,2.0,5 = 0,1. Отложите в сторону цифры а, в, значения этих углов, переносную скорость и точку переносного ускорения. Относительное движение поршня простое, поэтому проекция относительной скорости на касательную к траектории самолета определяется как производная по времени от относительных координат.
Сырья, промышленности и энергетики-х=: −10 * грех 2р. Т. Проекция относительного ускорения поршня равна производной 2-го порядка от относительной координаты времени Вт, х = Си = = −20 * — потому что 2〜т Движущаяся точка совпадает с моментом ускорения этой точки в неподвижной системе координат. Кориолисово (или вращательное) ускорение вычисляется по формуле Туалет = — ^ Е Х(**) Где σ^ 1-вектор угловых скоростей в переносном движении, а vr-вектор относительной скорости точек.
Значение ускорения Кориолиса туалет = грех ВР). (3 *) Направление ускорения Кориолиса определяется регулярностью векторного произведения. Ускорение Кориолиса wc, o> и vri направлено перпендикулярно плоскости, вектор наблюдателя, стоящего вдоль wc, является вектором ( ® , вектор vr pa минимальный угол направлен против часовой стрелки).P, которая определяет направление ускорения Кориолиса как векторное произведение.
Правило Е. Жуковского применяется для нахождения направления этого ускорения, которое существует. Относительная скорость vr проецируется на плоскость. Перпендикулярно угловой скорости, поверните проекцию этой плоскости на угол 90°в направлении вращения, определяемом<i) tf. Это будет направление ускорения Кориолиса.
Если траектория точки в движущейся системе координат не является линейной и относительное движение точки также искривлено, то переносное ускорение рекомендуется вычислять как геометрическую сумму нормальных и тангенциальных переносных ускорений. Относительное ускорение представляет собой геометрическую сумму нормали и касательной относительно acceleration. In в этом случае выражение (I *) записывается следующим образом: У = с wcn мы, — Ф внешт водонепроницаемые.
— j-wc, (4 *) За заданное время относительная скорость и ускорение приведены в таблице ТП = о Около 20… ’ (Т = 0.25 = 0.5 — Юг. 0. 0 2У * а На рисунке отложены относительная скорость и относительное ускорение. Относительная скорость и относительное ускорение тангенциально направлены к траектории. Их положительное направление совпадает с соотношением фиг-подобных скоростей. Ускорения Кориолиса равны туалет-2 0. Вектор ускорения Кориолиса по радиусу от центра (па. Б) к postpone.
At в каждый момент времени находят абсолютную скорость поршня и величину абсолютного ускорения, а также направление этих векторов. если n = 0 в = 0/25 7 ’= ve-vr = 160-I ^ 128,6 м / с, от w = — wc = 32-4 «19,44 М»; s \ / > 5 = 0,5 ж = \ Вт? — r Wr =Vx32 * 400t1 201 м / ССК *、 Углы а и А измеряются между направлением абсолютного ускорения и радиусом, соединяющим центр изгиба о с плоскостью М. Задача 5. 18.Корабль плывет по меридиану CBN с юга на север. Скорость до дна составляет 36 км}часов. Определите составляющие абсолютной скорости и абсолютного ускорения корабля с учетом вращения Земли вокруг своей оси.
Splat место Р Безразмерная скорость передачи произведения произведения угловой скорости Земли и радиуса вращения АВ вращается за 24 часа 1: ве = АБ-уе = Р соз 60°Щ)^ = = 64 ■ 10a♦0.5 24. п \ с = 232 миллисекунд(1) Эта скорость тангенциально направлена с запада на восток до 60-й Широтной параллели. Относительная скорость такая же. = 36 км / ч = 10 м \ с(2) И она граничит с C / W меридианом с юга на север. Определите составляющую абсолютного ускорения корабля.
Согласно теореме сложения ускорений, абсолютное ускорение равно уа =™Е «Р водонепроницаемые + Ratio motion-равномерное вращение вокруг оси, следовательно, отношение (fig-like acceleration) является отношением (ur-like normals Ускорение, его величина Да, = an•oj-e = R cos(> 0°ci) J = 64 * 108. 0.5 Ф — ^ = 0.017 Это ускорение направлено от B к L. Относительное движение происходит с постоянной скоростью по дуге окружности с радиусом R. таким образом, относительное ускорение становится обычным относительным ускорением, величина которого равна ТС = =-^ п м; сек * = 1.56 * 10 » S М’scc1.
Это ускорение направлено из точки B В точку O. ускорение Кориолиса определяется по формуле = Юг Значение ускорения Кориолиса, we = 2t » ev, sin (oC * V)=2йТ ® рёб10 sln60o = =’ 10 3 м! ССК. \ При расчете угла vr угловая скорость Земли была направлена вдоль оси вращения к Северному полюсу, поэтому мы рассматривали возможность получения угла 605 с vr. Ускорение Кориолиса направлено по касательной с востока на запад к параллельной линии на 60 градусах северной широты. Кроме того, рассмотрим случай, когда корабль плывет с запада на восток по параллельной линии 60 градусов северной широты. Предполагая вращение Земли посредством подвижного движения, как и прежде
Совместная скорость pa этого хребта тангенциально направлена к параллельным линиям (I (P северной широты, то есть направление совпадает с переносной скоростью). Размер и направление переносного ускорения соответствуют тому, что мы видели в предыдущем случае. Это относительное движение, pa, происходит вдоль дуги радиуса r cos 00°= AN. As в результате относительное ускорение становится нормальным, а величина-равной. Он направлен от B к A.
То есть направление совпадает с переносным ускорением. Ускорение Кориолпов равно туалет = 2sa, х Размер его я> с = 2г, г>, то Sin 90°= 1.46-10 м; УП \ co и vr не являются взаимно стоящими, поэтому они являются yarim * coriolis acceleration pa и anranleio или точкой B к A для этого time. So, все 3 составляющие абсолютного ускорения: wr, wn wc-направлены в этом случае вдоль 1 Прямой. Задача 5. 19.In в переходном режиме при запуске двигателя основного судна контейнер регулятора центрифуги Ватта (рисунок а) расходится и угол а изменяется по формуле е. а =(0 Куда?
Угол поворота контроллера вокруг вертикальной оси является функцией времени. (2) Где постоянный коэффициент k-0,3 сек — \длина стержня OA = = OB = AC = BC =-.i = 90 см. В момент^ = 10 секунд определите абсолютную скорость и абсолютное ускорение шарика регулятора. Это считается точкой. По Вопросу 3. 19. Решение. Абсолютное движение шара раскладывается на 2 движения: переносное движение-это вращение вокруг вертикальной оси, которое происходит по формуле(2), а относительное движение-это вращение вокруг горизонтальной оси ABC, которая проходит через точку O и происходит в соответствии с законом (I) Hor.
Выберите фиксированную систему координат обруча из точки O в качестве начала координат. ось x ориентирована перпендикулярно плоскости автономной адресной книги. (Около мгновения/ a,= 10 секунд) ось Y лидера-ось Z вправо по горизонтали в плоскости ABC-вдоль вертикальной оси вращения. Используя формулу(1), Находим значение угла a момента= 10 секунд. _ я^, т; 100_ а я)0 ′ — р! J00 не с Затем определите относительную угловую скорость проекции r на ось X. E. относительное вращение происходит на оси.
Эта проекция равна производной от угла a, но время Ш ^ = а = В0,-я-э \ т. Момент t \ = 10 секунд, проекция относительной угловой скорости Проекция относительного углового ускорения на одну и ту же ось x равна производной по времени от ıhh ghh = 1 ″ GC = * = 61 = lJ00 SSK〜\ Чтобы найти относительную скорость и относительное ускорение шара, мы мысленно останавливаем движение соотношения movementlike. Относительная скорость шарика ВР = ч \ Х = 90 = 2М: см! ы = м / с
Идентификаторы вэн, кол-доля, соответственно, нормальное ускорение в движение и относительное движение, WRX, на МРЛ. — Соответственно тангенциальному ускорению и соотношению фигуроподобного и относительного движения. Если вы используете теорему сложения ускорения, вы можете применить метод проекции. Если вы выберете фиксированную систему координат и проецируете уравнение (4*) на каждую из этих осей, вы увидите следующее: ™ах = ™ * ПХ-г-р wrnx я Р-х, 7Ф » ^ СХ> ™ay = Z’CNY + T «^ rny — \ — Wrxy ’ \ — Wl ™аз = „Вт-е т“ ^ РНЗ „Гwrxz“ 7 »
Абсолютный коэффициент ускорения определяется по формуле уа — \ РВ-колун «Гwiy + ж-a2t По(О*) Относительная скорость направлена перпендикулярно стержням OA и OB соответственно(рис. 6). Определите относительное ускорение шара. Поскольку относительное движение — это вращение вокруг оси, рекомендуется вычислять относительное нормальное ускорение и относительное касательное ускорение отдельно. Первый имеет тот же размер. внешт =нет, = = — см J sec1 0.0043 МС-с К1 n шаров будут направлены в точку O. величина относительного касательного ускорения выражается в Формуле РВ. = ч = 90 ^ = = — см / с * = г.10 3 м \ с *
Это ускорение совпадает с относительной скоростью и направлением движения каждого шара(рис. 6). Определите скорость и ускорение движения шарика. Переносным движением является вращение регулятора вокруг вертикальной оси по формуле(2). для расчета Отношение движения к движению, к скорости и ускорению мяча, относительно движения мысленно останавливается.
Проекция угловой скорости подвижного движения на ось вращения равна производной по времени от угла =: φ= Вт \ ty = 10 секунд, эта проекция 0) yy = 3•0.3.10 — = 90 секунд Проекция углового ускорения и переносного движения на ось вращения определяется как производная от этого времени «= * » =? = 6 **. На данный момент= 10 секунд ЭЭГ =6.0.3-10= 18 ССК \ Портативная скорость-это скорость шара, когда контроллер вращается вокруг вертикальной оси ОС. Размер равен произведению радиуса вращения и переносимой угловой скорости. Момент f j = 10 секунд ve-l sin ashe = 90 sin 30° * 90 = 40,5 м / с
Скорость перемещения шара направлена параллельно оси X. Для шара A он соответствует положительному направлению, а для шара B-отрицательному направлению оси (t = t). Переносное ускорение состоит из нормального ускорения и касательного ускорения. t = значение нормального переносного ускорения за 10 секунд Вэнь = / грех ал} = 90 греха 30° * 90 * см / С2 ^ 3645 м; сек. \
Направление кориолисова ускорения определяется по правилам векторного произведения. Ускорение Кориолиса направлено перпендикулярно плоскости, определяемой вектором o и vrt, причем наименьший угол от вектора поворачивается против часовой стрелки к vr pa. In в нашем случае ускорение Кориолиса направлено вдоль скорости транспорта (рис.6). Используйте проекцию, чтобы найти абсолютную скорость и абсолютное ускорение шара.
Найти проекцию абсолютной скорости на ось, проецируя векторное уравнение О Мяче А: vax r \ = 40,5 м / с, vay = — tv cos 30e = g-0,01 V ’ 6r. M секунд, va2 = vr cos60e = 0,01 t: M секунд размер абсолютной скорости Va = Vay-рвбз * * 40,51 м, сек Его направление определяется величиной направляющего Косинуса. потому что(оо = в = 0.999、 потому что {«Су)= х» г = −0.00 км、 °ля соѕ(α£*)= в°р — = 0.000775 в » ва Согласно теореме сложения ускорений, абсолютное ускорение Ва = Вт, н-ф Внешт Векс » ГWr、•
Если построить уравнение этого вектора на координатной оси, то найдем проекцию абсолютного ускорения шара А. Воск= — J-wc 17,9 м / с \ wuy = жировиков внешт грех 30° ~ водонепроницаемые. соѕ 30°я » 3G45 м / с \ = потому что 30е-Ф грех 30 0.0055°^ младший / МВ *. Величина и направление абсолютного ускорения определяются по обычной формуле. Г уа = Vwix + Вий ’ * * 3646 ЛГ / с <?*、 потому что («с») = 0.005、 Окей. в. потому что(УА,.у) = ^ 0,999、 tcy отсутствует. Да. потому что(^ а= 1.37.10 е. 2°.Скорость и ускорение точки в полярной, сферической или цилиндрической coordinates.
It рекомендуется для решения многих кинематических задач сложного движения точек в полярных, сферических и цилиндрических координатах.1 способ решения задачи о кривых координатах заключается в разложении абсолютного движения точки на подвижное относительное движение. Такая последовательность действий рекомендуется при решении задач данного раздела.
Необходимо определить абсолютное движение, учитывая относительное и соотношение фиг движения: 1) Выберите подвижную фиксированную систему координат. 2) Создайте относительное уравнение движения для точки. 3)создать уравнение соотношения движения. 4) получаем уравнение абсолютного движения и находим абсолютную траекторию движения точки. 5) определяет скорость точки во время относительного движения и ее портативную скорость. 6) найти абсолютную скорость и абсолютное ускорение точки, используя теорему сложения скорости и теорему к’орнолиса.
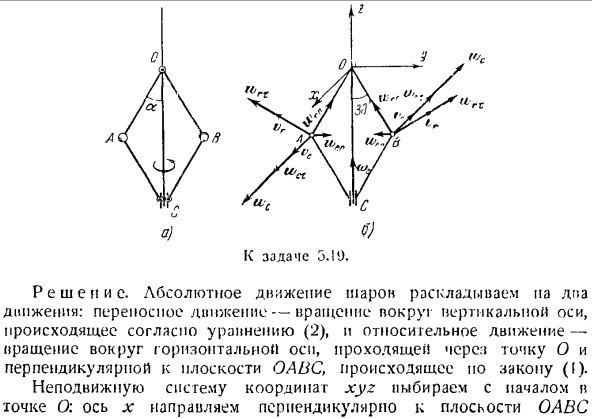
Задача 5. 20.Определите проекцию скорости точки M на естественное po полярной системы. Решение. Рассмотрим движение плоской траектории AN как сложное сложное движение, хотя это движение точки M. относительное движение-это линейное движение точки M вдоль Родиуса-веко-k: pa p. переносное двойное представление-это движение точки M с радиус-вектором, центрированным в точке O. найти проекцию относительной скорости точки pa в направлении радиус-вектора как производную по времени от радиуса vector. It называется радиальная скорая помощь и обозначается буквой В. Скорость передачи — это скорость выполнения задачи 5.20.
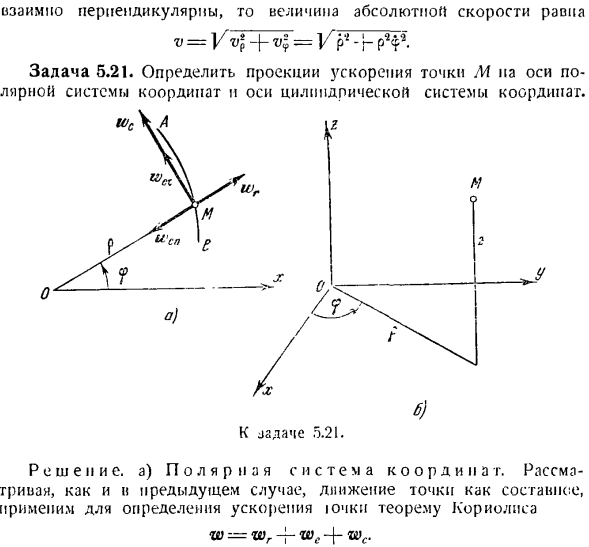
Рост неподвижных связанных точек м используйте радиус-проектор. Эта скорость, перпендикулярная радиус-вектору, называется скоростью trapsversalioP и имеет ту же величину. Абсолютная скорость точки M определяется как геометрическая сумма относительной и полезной скоростей. От этих скоростей Если они перпендикулярны друг другу, то величина абсолютной скорости равна Задача 5.21.Определите проекцию ускорения точки М на оси Полярной и цилиндрической систем координат. 6.) 5.21 к проблеме. Решение, а) полярная координата system.
As в предыдущем случае мы определяем ускорение ярма, применяя теорему корриола, принимая во внимание движение точек в виде соединения с = ТС-Ф-туалет-Джей-туалет Проекция относительного ускорения в направлении радиус-вектора имеет вид ЗР = Р Потому что относительное движение линейно. Это ускорение направлено вдоль радиус-вектора. Портативное ускорение составлено 2 co-accelerators. It смогите быть использовано в широком диапазоне применений.
Чань = Р? Переносное нормальное ускорение Вэнь = Р ’ Ф2. Вен (рис. е), направленный перпендикулярно радиус-вектору унитаза и направленный от точки М к центру вращения О. значение ускорения Кориолиса = TS9 разъем = ТС? (Потому что вектор a-это направление ускорения Кориолиса туалет = 2 (0 х ВР Соответствует переносному касательному ускорению. Затем находим проекцию точки ускорения на ось полярных координат. Проекция радиального ускорения ВФ = Вт-звеньев = п-п <Ф2.Проекция ускорения в направлении отлова обезьян% = «рввк = Р? — Я•= в ^(Р2?))-
Это проекции ускорения точки на оси полярных координат. б)п. И Л и НД р и Чески я системы координат. Иногда полезно использовать цилиндрические координаты траектории для пространственного движения точки. В этой системе координат, положение точки М определяется 2 полярные координаты р и СР, и 2 З(рис. Б).В этом случае проекция скорости точки определяется по формуле: В9 = ч, в? — =РФ=, П2 = з. Значение скорости r = V’VJ + W + rf. = В? + R’T K и его направление задается значением направляющего Косинуса потому что(в, п)= 9 -, потому что («Вэр)= — J, а потому что(к)=.
Индукционный Косинус равен потому что(УА, х)= ^ Т, потому что(УА, г)= — °г, потому что(зо, з)= СЖ . (?) Ай!) Заметим, что в случае поступательного движения угловая скорость этого движения®О= 2А. Для определения ускорения находим проекцию в цилиндрическую естественную по по следующему уравнению: Вт = р-р?,(си) ав = РС (7) = 2 =? (8)
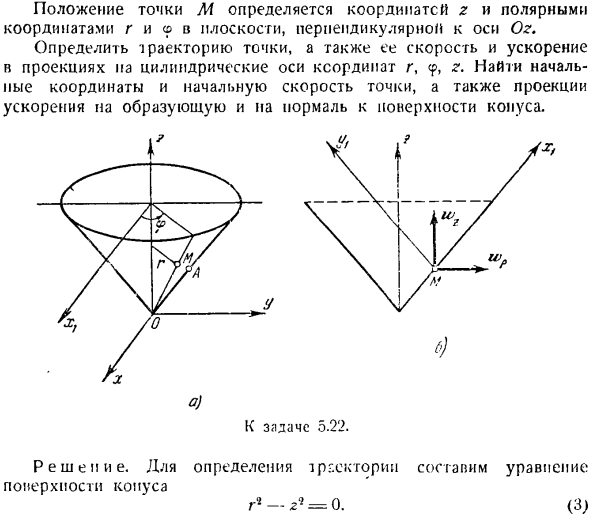
Кроме того, если вы различаете (li), это выглядит так: 1 ′ j. f-6. И затем… =(Ю) Погрузите (9) и(10)и (0), чтобы определить проекцию ускорения на радиальную ось Затем определите проекцию ускорения на ось ловушка-Базиль. После простой трансформации、 Подстановка этих значений в (7) выглядит следующим образом: В9 = 0. Из этого видно, что ускорение точки находится также на вертикальной плоскости, проходящей через ось симметрии конуса и рассматриваемой точки. Эта плоскость показана на рисунке.
a. выберите axis11x’] И Л/у. Выберите 1-й вдоль шины конуса, а 2-й вдоль нормали его поверхности. Найти проекцию суммарного ускорения точек на эти оси. После простого преобразования, это выглядит так: шхд = WР соз 45°-вес в COS 45°= с V’2 е * = в’2r = Оал Итак, проекция ускорения на генератор численно равна расстоянию точки от вершины конуса. Следующий 。 — л-4 |Л1а4/2 «4 шт.= — уа sin4®°ж-sin4® — = — — — грг = а•
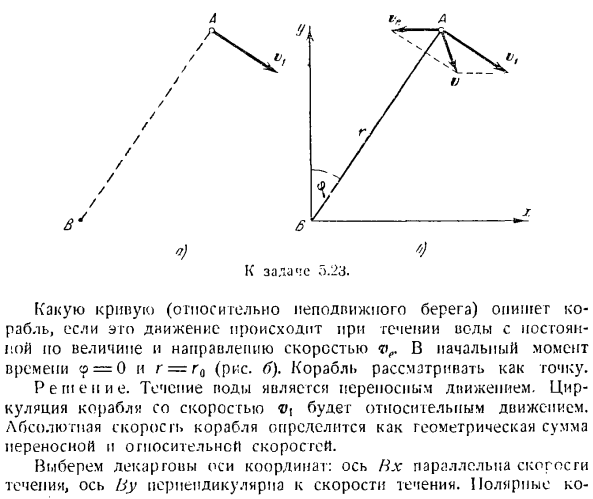
Задача 5.23.Скорость движения судна а к воде I постоянна по величине и всегда направлена перпендикулярно линии визирования в фиксированной точке P. Если это движение происходит, когда вода течет с постоянной скоростью и направлением vr в начальный момент времени<, какую кривую (для неподвижных берегов) описывает судно? — 0 и r = r0(рисунок B).Корабль считается точкой. Решение. Поток воды-это подвижное движение. Циркуляция судна со скоростью h) \ относительное движение. Абсолютная скорость судна определяется как геометрическая сумма переносной скорости и относительной скорости. Выберите декартову систему координат.
Их оси параллельны скорости потока, а ось by перпендикулярна скорости потока. Полярные районы Координаты корабля определяются радиус-вектором B A = r и углом yVA = Y. если спроецировать абсолютную скорость точки pa в направлении радиус-вектора и перпендикулярно ему: Ф = — ве грех <Р,(1) РБ = Ви-ЭП с COS <Р. (2) Если разделить уравнение (1) на уравнение (2), то получится: доктор ве грех c、 -= ———!- д’Ин. г ВВ-ве с COS В.、_ Эй’- ^ (3) при введении этой величины любой постоянной получается уравнение абсолютной орбиты корабля. 1 — Ви Или Р = Р0- 1 ve1 — COS » V、 Это ионный Поляр второго порядка equation.
It это странно. Метка кривой e = — равна коэффициенту cos 9 — Если<1, найденный локус представляет собой эллипс, а фокус «В» \ ке.В то время как параметры эллипса P = r0 \ 1—‘, параметры \ Я Эллипсоид определяется эксцентриком и полуосью a по формуле p = a(1-c).Равные этим 2 значениям параметры указывают длину полудлинной оси, перпендикулярной расходу. г. иа. — Ве. В ^ 1, траектория ginerbo. По начальным условиям, принятым в задаче («=0) ve = vy, абсолютные скорости движения судов в начальные моменты пуль равны.
Поэтому в этом случае корабль останется неподвижным.Однако, другая первоначального V Case data — = I соответствует параболической траектории движения жеппя корабль. Задача 5.24.Прямая d вращается вокруг точки Г с постоянной угловой скоростью w и перемещает кольцо M по эллипсу. Эллипсы a и b \являются фокусными точками эллипса F,а расстояние от центра до фокуса равно C. Определите коэффициент скорости точки M.
Решение.Полярное эллиптическое уравнение имеет грабли р = — р Я-потому что•? » Где pz = bilf’a-параметр эллипса, а e = c / a-показатель степени эллипса. Полярная ось отклоняется от фокусной G вдоль длинной оси эллипса (правая сторона рисунка).Модуль скорости точки в полярной координате равен V в = V в(、) После этого абсолютное ускорение может быть определено геометрически как задняя сторона многоугольника, построенная на векторе переносного ускорения, относительного ускорения и ускорения Кориолиса.
В противном случае это можно сделать с помощью описанной проекции above.To для этого достаточно спроектировать геометрический эквивалент 3 координатных осей (1) перпендикулярно друг другу, найти проекцию абсолютного ускорения этих осей по формуле (5), а также определить величину и направление абсолютного ускорения по формулам (6) и (7*).
При решении проблемы рекомендуется предпринимать такие действия.Мне это нужно.: 1) разложить движение на составляющие, определить абсолютное, относительное движение, соотношение фигура-подобное движению. 2) Выберите 2 системы координат: абсолютную и мобильную. 3) мысленно остановите переносное движение и определите ускорение и скорость точки в относительном движении. Если мы отличим его от эллиптического уравнения, то увидим, что: д-р_ мрэ греха dt (используйте 1-coso) -‘ С другой стороны, из Полярного уравнения это выглядит так: Д _ и> п (Это если что о Здесь. Ш =Г•. ДТ ’ Подставим значения (1) (2) и (3) в уравнение.
Мы получаем: в — — — — — — \ 1-р — е * — l2e потому что О-Е С COS <?) * 1 т Введя значения параметров P и эксцентриситета e в уравнение(4), получим, наконец.: В = а-р)р. Скорость-это касательная к эллипсу. Задача 5.25.Точка движется над поверхностью Земли со скоростью V. угол между скоростью и меридианом в каждой точке траектории постоянен и равен a. Определяет траекторию движения точки.
Задание 5.25 к. Решение. Декартовы координаты точки, движущейся вдоль сферы радиуса R, можно выразить в сферических координатах по формуле (рисунок а). х = р COS в 0, потому что г = р cosOsin З = Р $ в 0、 6-широта, cp-долгота расположения точки над сферой. Найдем представление скорости при постоянном радиусе R. R является производной декартовой координаты, но время равно л. х = р (- г, потому что грех-грех, потому что БФ), г = р (- грех, грех 0 <Р0-й-потому что с COS 6 <е), я = Р потому что ев.
Модуль скорости определяется отсюда = Vx1 vM7 ^ 1 = I Скорость v может быть разбита на 2 компонента. ВК = .- Р0.、 Касательная, направленная к меридиану, и r * 1 = R cos 0 $ ориентированный, но параллельный. В общем случае точки, движущейся вдоль сферы, модуль скорости выглядит так: в = ВВ] Но угол А, который образуется условиями материи, меридианом и скоростью, постоянен. Этот угол связан с составляющей скорости точки соотношением — =КТГ * в. б.
Или, после присвоения значения V, и Номер _ Rcos O — » ~ ~ Ctg: r» Когда вы изолируете переменную, она выглядит так: делать. 。 — ды на ктг. Косинус 0 Т Фе Это дифференциальное уравнение искомой орбиты. Предполагая, что начальная точка движения из положения<p0 = 0, 60 = 0 является интегральной: Шесть *\ \ — s = ctg a \ do J cos 9 * J•и Или Где я могу получить орбитальное уравнение
Кривая на поверхности сферы, описываемая этим уравнением, называется локсодромами. Это орбита корабля, Меридианы которого не меняются относительно меридианов. для clga ^ > () угол увеличивается бесконечно? Предельный угол определяется из уравнения%tO1C4 1 ″ 2 ″ = 1 Для этого.
Или 4) мысленно отвлекшись как от жены, так и от себя нахожу угловую скорость движения и ускорение точки соотношения фиг-подобное движение соотношения движение-подобное. 5) найти ускорение точки Кориолиса от известной угловой скорости переносной операции и скорости точки в относительном движении. 6) Используйте проекционный метод для определения проекции абсолютного ускорения на координатные оси.
7) используя проекцию обнаруженного абсолютного ускорения, найти искомое абсолютное ускорение по величине и направлению. Задача 5. 16.Цилиндр вращается с постоянной угловой скоростью (o) (>).Точка M движется вдоль поверхности цилиндра в соответствии с уравнением. Уравнения СИ-3, потому что 2-ХВ, г {Здж = м = 3 греха 0.) Поскольку координатная ось xh yit zx плотно соединена с цилиндром, она вращается с угловой скоростью o) 4 вместе с цилиндром. ось Z совпадает с осью симметрии.
Проекция на ось zj переносной угловой скорости равна » * lg (==2 сек. Определите абсолютную скорость и абсолютное ускорение точек AI. Если направление вращения цилиндра обратное, т. е.= m-2 sec’1, то как изменяется абсолютная скорость и ускорение точки M? Решение. Вращение цилиндра считается переносным движением. Движение точки А * 1 на поверхности цилиндра является относительным движением. На этом рисунке показана спираль, представляющая собой относительную траекторию движения точки AU, и определяется по формуле(I).
К выпуску 5. 15. Расстояние точки В от оси вращения Цзы r = V x’i + yi = z Скорость полезной нагрузки точки M — это скорость той точки цилиндра, где точка M в данный момент совпадает. ve = gy = 3-2 = 6 м / с. Эго-скорость находится в плоскости, перпендикулярной оси Z [t и касательной к поверхности цилиндра. Коэффициент УР целевой
Размер дождя в 2 раза превышает скорость сектора. Действительно, приращение площади сектора, описываемое радиус-вектором точки вдоль времени M (см. рисунок), достигает наименьшего 1-го значения. Д5 = 1 РСН= -!* РРД? =В Р3?,(5) Слово я- Где Dz-приращение дуги за период D/. Ограничьте отношение приращений площади к приращениям времени..
Как dS 1 1… а / ™о ДТ 2 и ДТ = 2-п? Есть секторная скорость. Далее мы переходим к преобразованию радиального ускорения точки. Это рассматривается в вопросе о случае Центрального движения、 Поэтому в этом случае локсодорома становится сферической спиралью, которая вращается вокруг Северного полюса. для ctga <^ 0 рассуждение, как и в предыдущем примере, равно 6 = — π / 2, а траектория представляет собой закрученную сферическую спираль. К выпуску 5.2 г. Пол.
Рисунок б. Локсодромия представлена проекцией на плоскость, перпендикулярную оси Z. Задача 5.26.Идентифицировать Ускорение перемещения точек Если плоскость, ее поперечное ускорение относительно центра O, равно пуле(движение таких точек называется Центральным движением). Решение. Используйте проекцию радиального и бокового ускорения, полученную в задаче 5.21. (Да (2) «П =? — РТ4. » «V = P? «Р 2 г = п-ДТ(П5 *)」 В зависимости от условия поперечное ускорение равно нулю n, следовательно, продукт не будет изменен Точка полного ускорения.
Уравнение для локуса полярных точек может быть выражено в виде зависимости Р = Р(?(7)) Таким образом, мы можем предположить, что радиус-вектор зависит от времени через промежуточную переменную д9
Где производная (4 \уравнение (1) за время (11)для радиус-вектора минус это значение 2-й производной?(4) заменяется значением из: *(12) Р 1 сделать. * Это равенство определяет ускорение точек с нейтральными лишайниками. Приводится представление длины ускорения через орбитальный и полярный элементы (7)и постоянной веерообразной скорости. Формула (12)I. It называется церемония виньетки, которую Ньютон получил впервые.
Задача 6. 27.Определите ускорение движущейся планеты по 3 законам Кеплера. 1.1. планета вращается вокруг Солнца по эллипсу, одним из ее фокусов является Солнце. 2.Площадь, описываемая радиус-векторами, идущими от Солнца к планете, пропорциональна времени их покрытия. 3.Квадрат орбитального периода планеты называется полуосевым кубом орбиты. Планеты и солнце считаются точками. Решение. Задача ускорения небесных тел в движении Кеплера также решается с помощью полярных координат.
Ось полюса Солнце доминирует из фокуса, расположенного вдоль большого естественного x эллипса. Форма уравнения эллипса в полярных координатах имеет вид П = Т + ПВ(1) Где п-б^’.a-параметр эллипса, c = c, ’ a-эксцентриситет эллипса, a и b-малая ось эллипса, а cx-половина фокусного расстояния. Второй закон Кеплера устанавливает мирскую норму гомеостаза 1de s-постоянная, равная 2-кратной скорости сектора.
Приступим непосредственно к расчету ускорения planet. By закон Кеплера, движение любой планеты является центральным. Дело в том, что скорость вращения вентилятора для большого Солнца постоянна, поэтому (Renspersalpa) составляющая ускорения планеты равна нулю, поэтому общее ускорение направлено на радиус. Таким образом, движение планет, сила второго закона Кеплера, является центральным movement.
To найдите ускорение планеты, примените выражение лозы (см. предыдущее задание). и… «(.Д-у \ У.=- Суу \ и-{-… П / 1 DTJ успешно Из уравнения (I) эллипса видно, что: 1 1 е И= — = — — — — — COS.」 Р 1 1> И затем… д-II и электронные. — да.»- — — — О COS < * В Следовательно、 ИД * а-_l, за Если ввести эти значения в Формулу Vinet, то она выглядит так: С -! , L и c2 w = wa= -; и. * — — — О. (2) Р \ * др ру * ’ Таким образом, ускорение планеты, движущейся по закону Кеплера, направлено к фокусу вдоль радиуса давления ярма. e.
It находится до Солнца, но светимость обратно пропорциональна мощности 2 расстояния до Солнца. Этот вывод можно получить из уравнения радиального ускорения (см. уравнение (I) предыдущей задачи) без использования формулы вине, дифференцируя эллиптическое уравнение (1) непосредственно по времени. Однако, этот nyib будет больше.
Формулу (’2) параметра p = b * fa можно заменить с помощью третьего закона Кеплера следующим образом: закон Кеплера 3 можно записать следующим образом: £=Λ,(3) Где a-полуосевая, T-орбитальный период планеты. k показывает постоянное отношение полу-длинноосного Куба к мощности 2 в цикле вращения. Период вращения при постоянной секторной скорости можно рассчитать, разделив площадь эллипса на эту скорость. Дж __ 2-АБ И
Подставляя значение периода в Формулу(3), получаем: 47.Вт’ 〜 Или Б1 _ _с хорошо-в 4 туи ’ Если ввести значение ego в уравнение (2), то оно должно выглядеть следующим образом: Идентификатор= Заметим, что в этой формуле константа k одинакова для всех планет Солнечной системы. Для задачи зарабатывания пешки в реальном времени и добавления ускорения мы рекомендуем»сборник теоретических задач» hi и следующие задачи. О, е-х а это и к » И. В. Мщерский, Лек здание с 1950 447、450、455、458、4 (51、462、467、473、479、481、483、488、490。
Смотрите также:
Предмет теоретическая механика

