Оглавление:















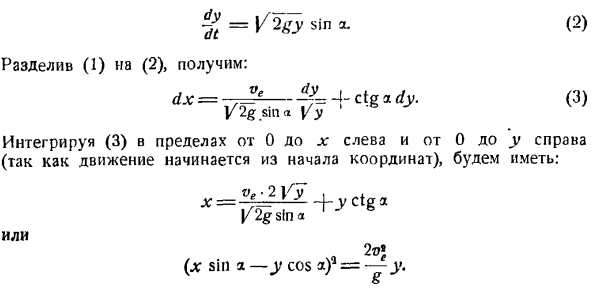




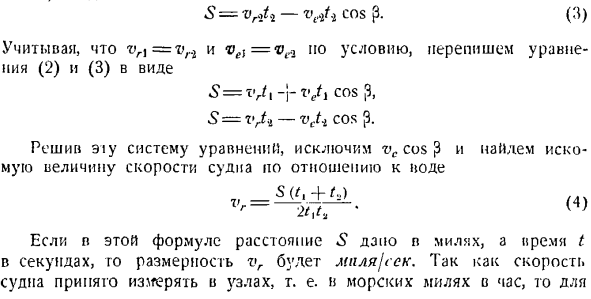




Сложение скоростей. Определение скорости точки в относительном, переносном и абсолютном движениях
- Прибавь скорость. Относительное движение, отношение относительного движения, определение скорости точки в абсолютном движении Соотношение между абсолютной, относительной и подвижной скоростями точек, выполняющих сложные (комплексные) операции, определяется сложением скоростей theorem.
By по этой теореме абсолютная скорость судна равна геометрической подвижной и относительной скорости. ва = veArvr(1 *) Чтобы определить относительную скорость точки, необходимо мысленно остановить переносное движение и рассчитать относительную скорость по правилам кинематики точки.
Чтобы определить переносимую скорость точек, достаточно мысленно остановить относительное движение и поиск. Людмила Фирмаль
Когда спутник стартует с поверхности Земли на экваторе, угол (Р = 0, следовательно、 vCi = 6400 * J/ 24•2 * / 36Q0 = 0,405 км / с Максимальная и минимальная относительные скорости спутников определяются из уравнения в = ВР±ВЭИ Или 8 = ВР = л 0.465; Где-максимальная относительная скорость ВР = 8.465 К. ujceK、 Минимальная относительная скорость г», = 7.535 К. ujceK. Если спутник стартует на широте 60°, то полезная нагрузка спутника равна скорости движения точки у поверхности Земли: vti = R cos 60°о>с = 0,233 км ’ сек、
Таким образом, наибольшая и наименьшая относительные скорости движения спутника определяются из уравнения 8 = ТВ±0,233、 Откуда? ВР НААН = 8.233 км! vr min = 7,767 км ’ секунд в сек Если спутник стартует с северного или Южного полюса, скорость транспорта будет равна нулю. Это связано с тем, что эти точки на земле находятся на оси вращения、 в-Б = 8 км! Считанные секунды. Задача 5. 10.Кривошип OA = g вращается в плоскости чертежа. = Ползунок A смешивается на наклонном звене B и может быть перемещен вперед вдоль естественного малого Oh.
- Угол наклона крыла относительно оси Ox равен a. Составьте уравнение для абсолютного и относительного движения точки А, найдите абсолютную скорость точки, относительную скорость и отношение скорости фиг. Решение. Первый способ. Абсолютное движение ползуна A-это вращение вокруг неподвижного центра O. относительное движение-это линейное движение ползуна вдоль заданного крыла. Переменное расстояние 0 {A = — q. переносное движение-поступательное движение точки A вместе с крылом.
Форма уравнения абсолютного движения точки А имеет вид х = rcoskt, г = РС \ НКТ. (1) С другой стороны, если вы представляете расстояние 001 = xe, это выглядит так: х = Хе — \ — м, потому что, г = м] грех. (2) Если мы решим уравнение (I) и (2) вместе, после простого преобразования, мы увидим, что: Грех Л * ^ — sTnT ’(3) йк,= / cosAtf-г грех КТ КТГ ОУ(4) точное уравнение (4), вплоть до определенного значения, является уравнением движения движения.
Удушение(3) — это уравнение относительного движения точки А. Людмила Фирмаль
Потому что последнее-это поступательное движение. 1-ДА / МММ В. ВМ / / В. Ш * один.) Выпуск 5. 10.To. Далее определяют абсолютную скорость точки А. vx = x = — rk sin kt, коэффициент абсолютной скорости = = РК потому что КТ、 в. В = УУ\ -} — м / * = РК、 Индукционный Косинус имеет следующий вид в COS(V, х)=〜= — грех КТ, потому что(v7y)= — = потому что КТ (5) Из (5) видно, что абсолютная скорость точки А перпендикулярна кривошипу ОА.
Проекция относительной скорости точки А в направлении 0, d равна производной по времени от относительной координаты потому что КТ vГг — = 7]= ГК-■-、 Гг> ’грех’ Потому что относительное движение легко. проекция переносной скорости точки A на ось x Векс =Хе = — R от греха КТ-Р К COS к-т КГН д、 Поскольку подвижное движение является поступательным, скорость всех сцен в крыле одинакова. 2-й способ. 1 1
Найти значение угловой скорости кривошипа ОА Вт = <в = к. Величина абсолютной скорости точки А как конца кривошипа вращающегося вокруг неподвижного центра О、 в = РМ = р к. Эта скорость направлена перпендикулярно кривошипу. Относительная скорость точки А находится вдоль прямой Окса. Скорость перемещения точки А параллельна оси Ox.
Создайте параллелограмм скорости (рисунок B).Отложите вектор, равный абсолютной скорости точки A. In на этом отрезке мы создаем параллелограмм скорости, как на диагональной линии. Эти значения определяются как стороны a parallelogram. By теорема синуса, она выглядит так: _ ВР_ есть ве грех потому, что КТ(КТ-я) ’
Отсюда найдите относительный коэффициент скорости потому что КТ проекция переносной скорости на ось x выглядит следующим образом: Векс = — РК(грех КТ-Ф-потому что КТ ктг я). При определении только абсолютного движения, отношения относительного движения, скорости относительного движения 2-й способ решения быстрее и проще приводит к цели. Если, кроме этих скоростей, нужно найти уравнения абсолютного, относительного и относительного движения, то рекомендуется применить первое решение.
Задание 6.11.Точка M скользит по наклонной плоскости призмы AB с относительной скоростью, а ее модуль равен Тг = учу> Где g-постоянный коэффициент, а^ — ордината точки, измеренная по вертикали от самой высокой точки prism. At в первый раз точка м находилась в точке а(рисунок а).Призма движется вправо с постоянной скоростью ve вдоль горизонтального пола. Для AC = h определите абсолютную траекторию движения точки M, абсолютную скорость момента касания пола. Решение.
Выберите абсолютную координатную ось, начало координат которой-точка A. ось Ax-горизонталь, ось Au-вертикаль, но вниз. Движение призмы АВС является переносным движением. Движение точки М относительно призмы является относительным движением. Построить на заданной мобильной скорости и относительной скорости Задача 5.11.Для. Точка L1 (рисунок b) параллелограмма, где диагональ-абсолютная скорость точки M. используйте чертеж, чтобы найти проекцию абсолютной скорости на декартову координатную ось.
ЧХ = вэ + ВР потому что, вы = ВР Си н я. Подставьте значения vn vx = dxjdt и vy = dyjdt в эти уравнения и перепишите их следующим образом: * Л = Вт + в * gyc ОСО(я) 2 = Vlgy грех х(2) Если разделить (1) на (2), то это выглядит так: ДХ = −7 ^ — $ = — \ — ctgzdy. (3) 2г грех \ г Если вы интегрируете (3) в диапазоне от 0 до x слева и от 0 до y справа (потому что движение начинается в начале координат), вы получите: ве. 2 Ат. 。
Или О б \ (х Sin а-у COS от Лу = — г. Это орбитальное уравнение. Локус представляет собой параболу оси симметрии n с вершиной в точке A, так как касательная в точке A горизонтальна(vy в начале движения равна нулю).Предполагая, что величина абсолютной скорости, с которой точка касается пола, равна этому моменту y = h, мы можем видеть из (1)и(2). П2 = я£+ т / J = 2gh + 2ве V7lgh потому что. Направление скорости определяется углом р в этой точке. Ctgp = ^ = ctga-i- vt. не доверяй своим глазам грех *
Задание 6.12. Штурман, находящийся в моей стреле морского экспедирования грузов, направляясь на северо-восток со скоростью 16 узлов, определил величину и направление различных относительных скоростей Контейнер. Эта относительная скорость равнялась V 2 узлам на 1 и была направлена на Запад. Определите величину и скорость абсолютной скорости корабля, то есть с телом Земли.
Узлы-это единица скорости, равная 1 морской миле за 1 час, а морская миля составляет 1852 м. Судно считается точкой. Вопрос 5.12 для. панрава-второй ошоши- Решение. Движение 2-го корабля считается сложным. Абсолютное движение 2-го корабля мы будем рассматривать как движение, связанное с Землей. Относительным движением 2-го судна считается его движение по отношению к перевозке груза.
Что касается переносного перемещения 2-го судна, то оно получает свою точку перемещения движущейся среды, которая прочно соединена с грузовым транспортным самолетом, которым 2-е судно является в настоящее время passing. In в данном случае переносным движением является перевозка грузов и поступательное движение. По условию задача известна:2-я относительная скорость Суда, обращенные на Запад: vr = 16] / 2 узла, скорость полезной нагрузки в поступательном движении, скорость груза ve равна-6 узлов, северо-восточное направление.
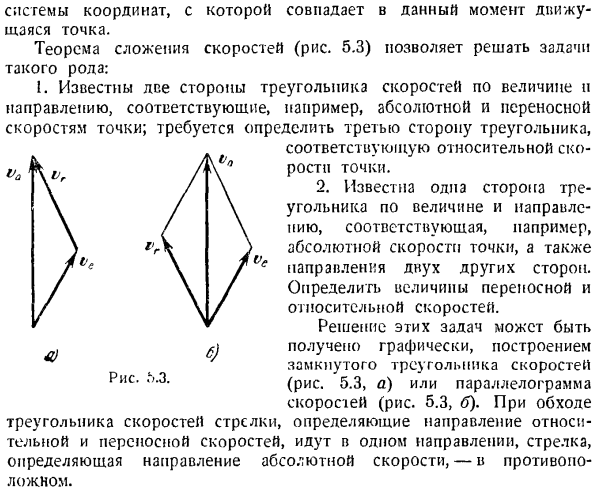
Согласно теореме сложения скоростей = + Чтобы графически найти абсолютную скорость 2-го корабля, создайте треугольник скорости (см. Рисунок). для этого, кроме любой точки A, скорость транспорта ve> Величину скорости и абсолютное и относительное отношение ur определяет 3-я сторона треугольника, соответствующая относительной скорости точки. 2.Размер и направление одной стороны треугольника соответствует, например, абсолютной скорости точки и направлению двух других сторон.
Определите значение переносной и относительной скорости. Решение этих задач можно получить графически, построив замкнутый треугольник скорости (рис. 5.3, а) или параллелограмм скорости (рис.5.3, б).При обходе треугольника скоростей стрелки, определяющие направление относительной и подвижной скорости, движутся в одном направлении, а стрелки, определяющие направление абсолютной скорости, — в противоположном.
Система координат, в которой точки перемещения в настоящее время совпадают. Такого рода теорема сложения скоростей(рис. 5.3): 1.2 стороны треугольника распознаются, например, в направлении, соответствующем скорости точки. Необходимый Может решить эту проблему б.) Фигура.\ 3.
Двигайтесь на северо-восток и отложите отрезок, равный. таким образом, треугольник скорости равнобедренный, а угол a = 90°. Поэтому абсолютная скорость направлена на Северо-Запад. Задача 6.13.При определении скорости судна относительно воды, судно специально оборудовано для измерения Задача 5.!L. It ’ ы время, чтобы сделать большую часть его! 2 прямые линии в противоположных направлениях друг к другу other.
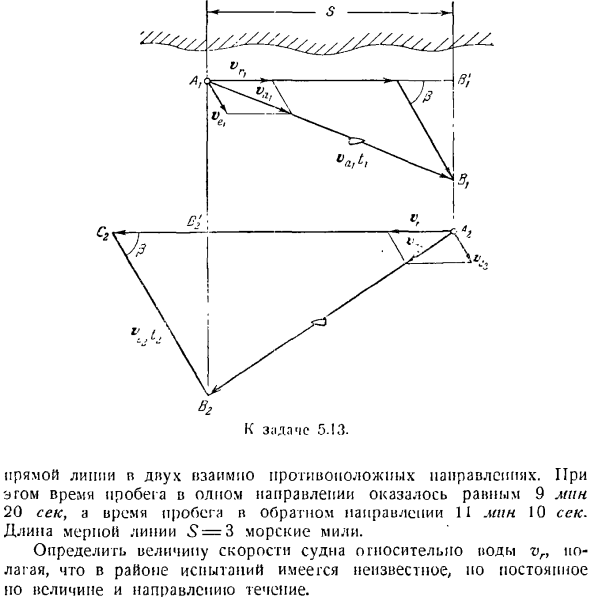
In в этом случае время в одну сторону составило 9 минут и 20 секунд, а в другую-время в пути составило 2 минуты и 10 секунд. Длина измерительной линии S = 3 морских мили. В зоне испытаний определяют величину скорости судна относительно воды vn, предполагая, что существует неизвестный, но постоянный поток по величине и направлению. The solution. Do вы считаете движение корабля более сложным? Что касается абсолютного движения кораблей, то они принимают движение по отношению к Земле.
Скорость этого движения dq, ни величина, ни направление не имеют значения. Для относительного движения кораблей, возьмите движение, связанное с городом. Относительная скорость vr измеряется в направлении (ориентированном вдоль линии измерения), обе величины неизвестны, и величина относительной скорости не изменяется в обоих прогонах. Для портативного движения сосуда, примите движение сосуда вместе с массой воды.
Скорость переноса ve равна скорости потока, ее величина и направление постоянны и неизвестны. Теорема сложения скорости записи Ву = вэ — \ — ВР. (1) Умножьте равенство этого вектора на время первого теста,、 Если спроецировать последнее уравнение в направлении измерительной линии s, то оно будет выглядеть так (см. рисунок): S = vrit,+ tvi ’ ic033, (2) Неизвестный угол между потоком и измерительной линией обозначается буквой P. Примените аналогичную технику ко 2-му прогону. Умножим время 2-го теста на векторное равенство (1)!И мы получаем: Ваик = Вра «» Л-
Если мы спроецируем равенство этого вектора в направлении измерительной линии s, то увидим, что: Ы = vrJ, 2-файта} потому что С. (3) Предполагая, что tvi = fr2 и vel = vt, 2, по предположению, перепишем уравнения(2)и(3)в виде: Ы = vrtl-rvet1 потому что 3, Ы = vrti-vcti потому что С. После решения системы уравнений AIY исключите vc cos exclude и найдите искомое значение скорости судна относительно воды. Если расстояние в этом уравнении задается милями, а время t-секундами, то размерность vr равна Миле / С.
Поскольку скорость судна обычно измеряется в узлах, то есть 1 миля в час、 Чтобы перейти к узлу, умножьте правую часть (4) на 3G00(количество секунд в 1 час)… ^ = 3600 узлов. ТИДЖЕЙ. ф Подставляя числовые данные/,= 0 минут 20 секунд = №#ssk,/ 2 = 11 минут 10 секунд/ s = 610 cetc, выглядит так: 3 (D) 60 4-670; 0,.LL ^ = T.-56O-67Oi3600 = I7 ’7 U3′ 13 ″ Задача 5.14.Корабль идет на восток со скоростью 12 узлов, и флюгер мачты показывает южный ветер.
Корабль меняет курс и идет на север с той же скоростью, но флюгер теперь показывает западные ветры. Н. Я… Один. О Компании −1- — — W 6.) Задача 5.14. в. Л’ IV. — Определите величину и величину скорости ветра относительно Земли с учетом постоянной скорости аллигатора. Примечание название курса указывает на пункт назначения судна, а название воды указывает на источник ветра.
Решение. Рассмотрим движение ветра как комплекс movement. As за абсолютное движение ветра он принимает его движение по отношению к Земле. Относительное движение ветра рассматривается как его движение относительно движущегося судна. Для портативного движения ветра, мы принимаем движение вместе с двигая кораблем. Абсолютная скорость ветра не известна ни по величине, ни по направлению. Относительная скорость ветра vr известна только в направлении 2 точек.
Размер и направление переносной скорости ветра, равной скорости движущегося судна, известны в одной и той же точке ve. Согласно теореме сложения скоростей является: = = + * > г Итак, в первом курсе корабля теорема сложения скорости ветра описывается следующим образом: И-О.) Выполните построение, соответствующее правой части Формулы (1).Отложите хорошо известный вектор vel и нарисуйте направление вектора от края (рисунок A). Опишите теорему сложения скорости ветра во 2-м курсе корабля. «Че! = Вет-я — » Г * Структура справа от этого уравнения показана на рисунке. a. In кроме того, есть обе диаграммы, которые совместимы.
То есть мы выполняем построение обоих сразу из 1 точки А. Далее начало вектора vn совпадает с точкой A, а пересечение направлений vrl и vrl определяет конец вектора vit(рисунок C).Согласно условиям, абсолютная скорость ветра постоянна. мы фабрика начала Китая. Е. =это учитывается при построении диаграммы. с. с носа полива видно, что ветер юго-западный. Его скорость равна va = 12 U ’ 2 узла= 12 U2™м / с, например ъ8. 73 м / с. Для овладения навыками решения задач сложения скоростей рекомендуется решать из задач, следующих за y-in и»сборником задач по теоретической механике».
Таким образом, решение сводится к построению треугольного или параллелограмма скорости и определению элементов, сторон и углов этих геометрических фигур. Это определение может быть сделано с помощью тригонометрии или путем проецирования геометрического эквивалента (1) в декартову систему координат.
При применении проекции необходимо выбрать оси и спроектировать равенство (1) этих осей. Затем зависимости между абсолютной скоростью, относительной скоростью и переносными предсказаниями скорости определяются уравнением. (с *) в = 1 / в 4-е *. Огайо. И вы. Величина абсолютной скорости находится в ее проекции Направление абсолютной скорости определяется Косинусом направления в. (4 *) потому что, к, Х) = соѕ(ва, г)=
При решении задачи рекомендуется следующая последовательность действий: 1) разложить движение на составляющие, определить абсолютное, относительное движение, соотношение фигура-подобное движению. 2) Выберите 2 системы координат: абсолютную и мобильную. 3) переносное движение, которое мысленно останавливается и находит скорость движения относительно точки. 4) отвлеките внимание мысленно от относительного движения и найдите скорость движения по соотношению движения точек. 5) примените теорему сложения скоростей и определите абсолютное значение точки по формуле.
Если вы знаете абсолютную скорость, вы можете использовать теорему сложения скорости, чтобы найти желаемую относительную или переносную скорость точки. Задача 5.8.Действительно, половина лодок плывет одна за другой с расстояния s на другую с одинаковой скоростью I>.Задняя лодка. Звук локатора, прикрепленного к 4, догоняет плавучую лодку в точке B \ n и отражает ее обратно на экран локатора в точке Ax. Я… Я, Я, У. * _ С В. В. 0.) 5. 8 3Д коттеджей. один.) б.)
Если скорость звука в воде равна s, то определяется время между выходом звука из A и возвращением в Alf. Решение. Первый способ. Давайте разберем абсолютное Движение звука на определенной скорости с переносным движением, которое сочетает в себе движение относительно передней лодки и передней лодки. Подвижная скорость равна скорости первой лодки, v, поскольку движущаяся система координат связана с первой лодкой и движется постепенно.
Когда звук распространяется от задней к передней части лодки, относительная скорость звука (рисунок а) Б1 =с-В. При такой относительной скорости звук слышен в момент времени t {.So … (с-V) У = Ы. (1) В противоположном направлении, от передней к задней части лодки, звук имеет относительную скорость(рисунок B) ври = с — \ — V и、 В этом случае, поскольку абсолютная скорость звука с направлена вправо, а подвижная скорость задней лодки I направлена влево.
Звук перемещает относительное расстояние s между лодками в кормовой части на некоторое время. (С + в) Т.2 = с. (2) Определите время tb от времени tx и (1) от времени tx и (2), Добавьте их и найдите время, необходимое для его возврата с аудиовыхода. 4_4•в _ ы. _2 с СК I-Г1-i-о — — -!-г— 5-с—. 1’C-V 1 C — \ — V C * — V 2-й способ. Время, за которое звук проходит расстояние AB \t (рисунок C).Расстояние от этого. ABx = ctb(3) С. потому что звук проходит этот путь с постоянной скоростью.
С другой стороны, такое же расстояние будет равно начальному расстоянию между лодками AB, плюс расстояние BB \ U, которое предыдущая лодка прошла во времени tx на скорости v. Абы = с + вю. (4) Если приравнять (3) и (4), то можно увидеть следующее: t. 2 показывает время, когда звук проходит расстояние BiAlt, отраженное от передней лодки. Это расстояние BxAx = СТВ(г) Звук-это время t. потому что мы переместились на это расстояние с постоянной скоростью c на y, тогда как это расстояние ВХА, = авг-AAL = s VT, — R » ( * , — F U), (7)
AA-это путь, по которому обратная лодка проходит с постоянной скоростью v в течение времени (tx — (-1^)), поэтому если сравнить равенства (6) и (7)、 с-[- V в в V(Т Я-J— Время, необходимое от аудиовыхода из A для возврата в A \, равно сумме времени t \и f2 Если подставить в эту формулу значение tu, которое определяется из (5), то、 Л= А затем решить(8)относительно неизвестного неизвестного t, и после простого преобразования、 2сц. Да. 1 /? г / т] V. 1. Да. И затем/ С » — В1
Как видите, первый метод, который основан на теореме сложения скоростей, становится желтым, потому что он проще и быстрее. Задача 5.9.При запуске искусственного спутника Земли он должен быть проинформирован об абсолютной горизонтальной скорости 8 км / ч вблизи поверхности Земли. Он определяет минимальную и максимальную относительную горизонтальную скорость, которая должна быть сообщена спутнику, если запуск происходит на экваторе. На широте 60°; на Северном полюсе. Радиус Земли#= 6400 км.
Решение. Спутник вращается в унисон с Землей перед полетом. Движение спутника вдоль земли считается подвижным движением. Рассмотрим движение спутника относительно Земли как относительное движение. Абсолютная скорость спутника выглядит так: = К выпуску 5.9. С-В. Угол широты стартовой площадки<?Выражается в, и полученное уравнение позволяет определить максимальную относительную скорость в-ВР-ВЭИ Куда? ве = Р COS в <РКК. (])
Смотрите также:
Предмет теоретическая механика

