Оглавление:
Сложение пар. Условие равновесия системы пар
Как уже говорилось выше, пара есть такая система сил, которая не может быть упрошена, т. е. заменена одной силой. Поэтому в механике, наряду с действиями над силами, приходится рассматривать и действия над парами сил. Аналогично соответствующим понятиям для сил, операция замены системы пар одной эквивалентной парой называется сложением пар. Пара, действие которой на тело заменяет действие на него всех данных пар вместе взятых, называется результирующей парой.
Теорема. Действие на тело нескольких пар, лежащих в произвольных плоскостях, эквивалентно действию одной пары, момент которой равен геометрической сумме моментов составляющих пар.
Доказательство. Рассмотрим сначала сложение двух пар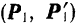 
и 
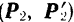, лежащих в пересекающихся плоскостях 
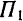и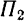 
с моментам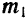и 
и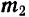 
(рис. 42).
Переместим каждую из данных пар в ее плоскости так. чтобы плечи пар совпали с линией пересечения плоскосте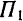й и 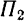. Возьмем теперь на этой линии произвольный отрезок 
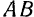и примем его за общее плечо обеих пар, изменив, конечно, соответствующим образом модуль сил, составляющих пары. При этом должно быть: 
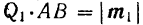и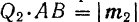 
.
Сложив силы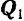 
и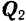 
, приложенные в точке 
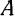, получим равнодействующую 
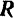, сложив силы 
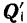и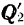 
, приложенные в точке 
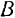, получим равнодействующую 
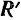. Вследствие равенства и параллельности соответствующих сторон силовых параллелограммов очевидно, что равнодействующие 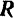и 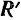равны по модулю и параллельны. Кроме того, они направлены в противоположные стороны.
Таким образом, в результате сложения двух данных пар мы получим новую, результирующую пару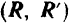 
, лежащую в некоторой плоскости 
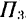, не совпадающей ни с одной из плоскосте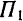й и 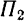. Так как
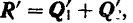
то момент результирующей пары
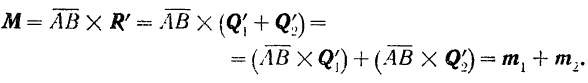
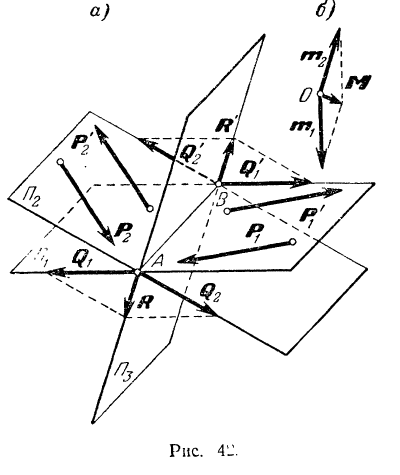
Таким образом, момент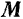 
результирующей пары равен геометрической сумме моментов составляющих пар, т. е. изображается (рис. 42, б) по модулю и по направлению диагональю параллелограмма, построенного на моментах составляющих пар.
Доказанное для двух пар легко распространить и на случай, когда на твердое тело действует в различных плоскостях любое число пар. Перенося моменты этих пар как свободные векторы в одну общую точку и последовательно складывая их, подобно тому, как мы складывали силы, сходящиеся в одной точке, мы приходим к правилу, аналогичному правилу сложения сходящихся сил:
Момент 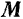результирующей пары изображается по модулю и направлению замыкающей стороной многоугольника, построенного на моментах составляющих пар как на сторонах, т. е. является геометрической суммой моментов составляющих пар:
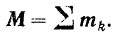
Очевидно, что если пары, действующие на твердое тело, взаимно уравновешиваются, то момент 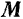их результирующей пары должен равняться пулю.
Отсюда следует, что Оля равновесия системы пар, расположенных как угодно в пространстве, необходимо и достаточно, чтобы равнялась нулю геометрическая сумма их моментов, т. е. чтобы многоугольник, построенный на моментах данных пар, был замкнутым.
Пример задачи:
На твердое тело действуют три пари сил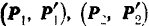 
и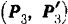 
, расположенные в трех взаимно перпендикулярных плоскостях (рис. 43,а). Модули сил пары, расположенной в плоскости 
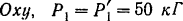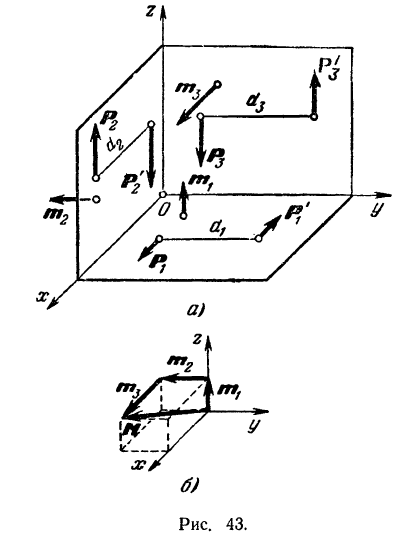
. Плечо этой пары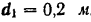 
. Модули сил пары, расположенной в плоскости 
,
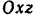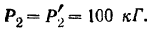
Плечо этой пары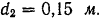 
. Модули сил пары, расположенных в плоскости 
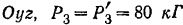. Плечо этой пары 
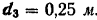. Найти результирующую пару.
Решение:
Находим модули моментов составляющих пар:
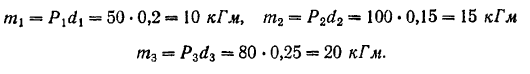
Выбираем какой-либо масштаб для модуля моментов и изображаем моменты пар в виде векторов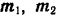 
и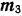 
(рис. 43,а), направленных в соответствии с установленным выше (стр. 61) правилом.
Так как моменты 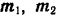и 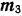составляющих пар расположены по трем взаимно перпендикулярным направлениям, то момент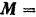 
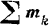результирующей пары изобразится диагональю соответствующего параллелепипеда (рис. 43,6). Модуль этого вектора
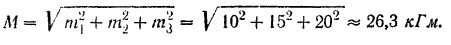
Плоскостью действия результирующей пары может быть любая плоскость, перпендикулярная вектору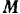 
ее момента. Проекции вектора 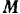момента на выбранные оси координат (рис. 43,6) нам известны: 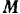{20, —15, 10}. Следовательно, уравнение семейства плоскостей, перпендикулярных вектору 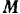, запишется в виде: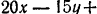 
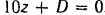, где 
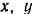и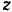 
—текущие координаты точек плоскости и 
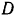— произвольная постоянная.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
| Теоремы об эквивалентности пар |
| Момент пары как вектор |
| Момент силы относительно центра (точки) |
| Теорема о параллельном переносе силы. Главный вектор и главный момент произвольной системы сил |
