Оглавление:
Сложение мгновенных вращений, оси которых пересекаются
Рассмотрим мгновенное вращение твердого тела Т относительно системы 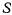 с мгновенной угловой скоростью
с мгновенной угловой скоростью 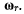 Пусть система
Пусть система 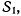 сама совершает мгновенное вращение с мгновенной угловой скоростью
сама совершает мгновенное вращение с мгновенной угловой скоростью 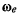 относительно некоторой неподвижной системы отсчета
относительно некоторой неподвижной системы отсчета 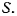 Предположим, кроме того, что линии действия векторов
Предположим, кроме того, что линии действия векторов 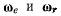 пересекаются в некоторой точке О. Рассмотрим скорость произвольной точки М твердого тела Т, совершающей вместе с телом сложное движение. Движение тела Т относительно системы
пересекаются в некоторой точке О. Рассмотрим скорость произвольной точки М твердого тела Т, совершающей вместе с телом сложное движение. Движение тела Т относительно системы 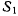
представляет собой мгновенное вращение с мгновенной угловой
скоростью 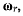 поэтому относительную скорость точки М получим
поэтому относительную скорость точки М получим
из уравнения
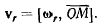
Величина и направление переносной скорости точки определяются из условия, что подвижная система отсчета тоже совершает мгновенное вращение с угловой скоростью 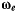 относительно системы S. Поэтому переносная скорость точки М будет равна
относительно системы S. Поэтому переносная скорость точки М будет равна
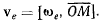
На основании теоремы о сложении скоростей теперь будем иметь
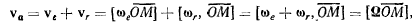
т. е. скорость произвольной точки твердого тела определяется фор-
формулой
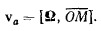
Как мы уже знаем, такое движение является мгновенным вращением с мгновенной угловой скоростью 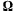 . Вектор результирующей мгновенной угловой скорости
. Вектор результирующей мгновенной угловой скорости 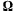 равен геометрической сумме векторов относительной и переносной угловых скоростей, т. е.
равен геометрической сумме векторов относительной и переносной угловых скоростей, т. е.
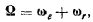
а его линия действия проходит через точку О. Итак, если твердое тело совершает сложное мгновенное движение, состоящее из двух
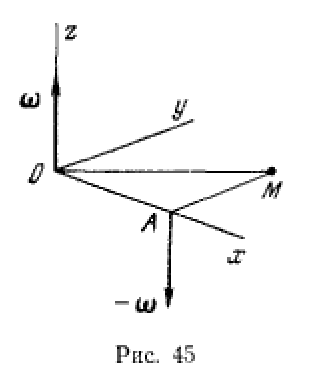
одновременных вращений с угловыми скоростями 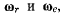 линии действия которых проходят через одну и ту же точку О, то результирующим движением будет также мгновенное вращение с мгновенной угловой скоростью
линии действия которых проходят через одну и ту же точку О, то результирующим движением будет также мгновенное вращение с мгновенной угловой скоростью 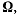 , которая представляет собой сумму мгновенных угловых скоростей
, которая представляет собой сумму мгновенных угловых скоростей 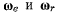 с линией действия, проходящей через точку О. Отсюда следует, что векторы
с линией действия, проходящей через точку О. Отсюда следует, что векторы 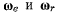 можно переносить вдоль их линий действия и складывать по правилу параллелограмма, если их линии действия пересекаются, т. е.
можно переносить вдоль их линий действия и складывать по правилу параллелограмма, если их линии действия пересекаются, т. е. 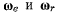 векторы скользящие. Распространяя правило сложения векторов на случай трех и более вращений, получим следующую теорему. Теорема. Если твердое тело Т совершает мгновенное вращение с угловой скоростью
векторы скользящие. Распространяя правило сложения векторов на случай трех и более вращений, получим следующую теорему. Теорема. Если твердое тело Т совершает мгновенное вращение с угловой скоростью 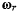 относительно системы
относительно системы 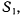 которая сама вращается с угловой скоростью
которая сама вращается с угловой скоростью 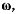 относительно системы
относительно системы 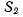 система
система 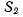 совершает мгновенное вращение относительно системы
совершает мгновенное вращение относительно системы 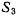 и т. д., и, наконец, система
и т. д., и, наконец, система 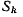 совершает мгновенное вращение
совершает мгновенное вращение
относительно системы 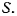 с угловой скоростью
с угловой скоростью 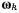 и если линии
и если линии
действия векторов 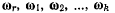 и пересекаются в одной точке, то результирующее движение твердого тела является мгновенно-вращательным движением с угловой скоростью
и пересекаются в одной точке, то результирующее движение твердого тела является мгновенно-вращательным движением с угловой скоростью 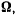 которая определяется как геометрическая сумма векторов, т. е.
которая определяется как геометрическая сумма векторов, т. е.
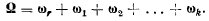
В частном случае, когда твердое тело участвует в двух мгновенных вращениях в противоположных направлениях с одинаковыми по величине угловыми скоростями, результирующее движение будет соответствовать состоянию покоя (система будет вращаться в одну сторону, а твердое тело вокруг той же оси — в противоположном направлении).
Следствие. Добавление (или отбрасывание) к системе движений твердого тела двух равных мгновенных вращений в противоположных направлениях не меняет мгновенного распределения скоростей в твердом теле. Рассмотренные свойства мгновенных вращений позволяют установить кинематический смысл эквивалентных систем скользящих векторов 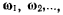
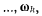 который соответствует одному и тому же результирующему мгновенному движению твердого тела.
который соответствует одному и тому же результирующему мгновенному движению твердого тела.
Пара вращений
Пусть мгновенное движение твердого тела является сложным и состоит из мгновенного вращения подвижной системы координат 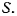 вокруг неподвижной оси (пусть для определенности эта ось совпадает с осью z) с мгновенной угловой скоростью
вокруг неподвижной оси (пусть для определенности эта ось совпадает с осью z) с мгновенной угловой скоростью 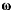 и мгновенного вращения в этой системе твердого тела
и мгновенного вращения в этой системе твердого тела
вокруг оси, параллельной оси вращения системы S (параллельной оси г), но в направлении, противоположном вращению системы S (рис. 45). Предположим, что величина мгновенной угловой скорости вращения твердого тела относительно системы S равна величине мгновенной угловой скорости вращения подвижной системы S. Такое мгновенное движение можно представить двумя скользя- скользящими векторами 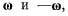 равными по величине, направленными в противоположные стороны и лежащими на параллельных прямых. Определяя скорость произвольной точки М твердого тела по теореме о сложении скоростей
равными по величине, направленными в противоположные стороны и лежащими на параллельных прямых. Определяя скорость произвольной точки М твердого тела по теореме о сложении скоростей
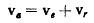
и имея в виду, что подвижная система осей совершает мгновенное
вращение со скоростью 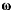 переносную скорость точки М определим
переносную скорость точки М определим
по формуле Эйлера (рис. 45)
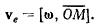
Мгновенное относительное движение тоже является мгновенным
вращением, поэтому относительная скорость точки равна
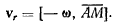
Для определения абсолютной скорости получим соотношение
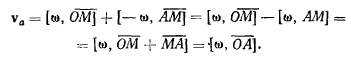
Нетрудно видеть, что величина и направление скорости произвольной точки твердого тела, участвующего в таком движении, не зависят от ее положения, а зависят лишь от расположения осей вращения. Скорости всех точек твердого тела оказываются равными по величине и по направлению. Такое движение твердого тела называется мгновенно-поступательным движением. Результат можно сформулировать в следующей теореме. Теорема. Пара мгновенных вращений твердого тела эквивалентна одному результирующему мгновенно-поступательному движению, скорость которого равна по величине и направлению моменту этой пары.
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:
Предмет теоретическая механика
Эти страницы возможно вам будут полезны:

