Сложение двух параллельных сил, направленных в одну сторону
Правило параллелограмма сил для сложения параллельных сил непосредственно неприменимо, так как точка пересечения параллельных сил лежит в бесконечности.
Для того чтобы вывести правило сложения двух параллельных сил, заменим эти силы эквивалентной системой двух сходящихся сил. Рассмотрим сначала систему двух параллельных сил, направленных в одну сторону (рис. 31). В точках приложения этих сил 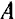 и
и 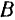 приложим две равные по модулю силы
приложим две равные по модулю силы 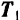 и
и 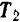 , направленные в противоположные стороны но прямой
, направленные в противоположные стороны но прямой 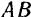 . Сложив теперь по правилу параллелограмма силу
. Сложив теперь по правилу параллелограмма силу 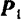 с силой
с силой 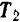 и силу
и силу 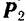 с силой
с силой 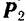 , получим две сходящиеся силы
, получим две сходящиеся силы 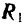 и
и 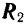 . Перенесем силы
. Перенесем силы 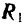 и
и 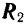 вдоль их линии действия в точку
вдоль их линии действия в точку  пересечения этих линий. Для определения модуля и положения равнодействующей
пересечения этих линий. Для определения модуля и положения равнодействующей
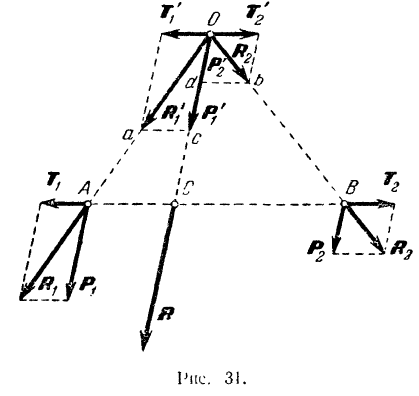
данных сил произведем теперь обратные действия: силу  разложим па две составляющие, параллельные силам
разложим па две составляющие, параллельные силам 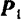 и
и 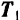 а силу
а силу 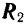 — на составляющие, параллельные силам
— на составляющие, параллельные силам 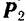 и
и 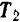 . Из попарного равенства параллелограммов, построенных при точках
. Из попарного равенства параллелограммов, построенных при точках 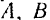 и
и 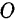 , следует, что полученные составляющие
, следует, что полученные составляющие 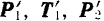 и
и 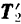 соответственно равны по модулю силам
соответственно равны по модулю силам 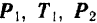 и
и 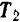 . Таким образом, система двух параллельных сил свелась к системе четырех сил. приложенных к одной точке
. Таким образом, система двух параллельных сил свелась к системе четырех сил. приложенных к одной точке 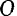 .
.
Равные по модулю и направленные по одной прямой в противоположные стороны силы 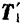 и
и 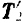 , взаимно уравновешиваются, и их можно отбросить. Остаются две силы
, взаимно уравновешиваются, и их можно отбросить. Остаются две силы 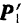 и
и 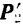 , направленные по одной прямой в одну сторону. Их равнодействующая
, направленные по одной прямой в одну сторону. Их равнодействующая 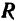 направлена по той же прямой, параллельной линиям действия данных сил, в туже сторону и по модулю равна сумме их модулей
направлена по той же прямой, параллельной линиям действия данных сил, в туже сторону и по модулю равна сумме их модулей
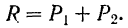
Найдем теперь, где проходит линия действия равнодействующей, для чего определим положение точки  пересечения этой линии с прямой
пересечения этой линии с прямой  . Из подобия треугольников
. Из подобия треугольников 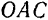 и
и 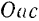 следует
следует 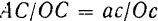 или, принимая во внимание пропорциональность сторон силового треугольника модулям соответствующих сил,
или, принимая во внимание пропорциональность сторон силового треугольника модулям соответствующих сил,
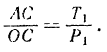
Из подобия же треугольников 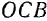 и
и 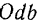 следует:
следует:
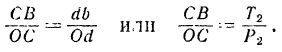
Разделив первую пропорцию на вторую и принимая во внимание, что 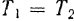 , получим
, получим
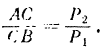
Следовательно, точка 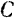 делит прямую
делит прямую 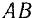 на части, обратно пропорциональные составляющим силам, и мы, таким образом, приходим к правилу:
на части, обратно пропорциональные составляющим силам, и мы, таким образом, приходим к правилу:
Равнодействующая двух параллельных сил, направленных в одну сторону, им параллельна, направлена в ту же сторону и равна по модулю сумме их модулей; линия действия равнодействующей лежит между линиями действия составляющих сил на расстояниях от них, обратно пропорциональных модулям этих сил.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:

