Оглавление:




















Сложение движений. Определение траекторий и уравнений движения в относительном и абсолютном движениях точки
- Добавление движения. Определение траектории и уравнений движения в относительном и абсолютном движении точек Уравнение движения точки M в относительном движении выражается формулой * 1 = ф.(0> Г \ = М).Да.」 Где xi y \ — координата движущейся точки M в относительной системе координат 0 \ X \ yxzx (рис. 5.1). Исключите время из этих аннуитетов, чтобы определить траекторию абсолютного движения.
У нас есть: Р потому что КТ, УГ = Р%\ Vlkt. Площадь каждого из этих уравнений, и далее найти орбитальное уравнение 2 грамма Это уравнение эллипса, ось симметрии которого параллельна оси Oy, и находится на расстоянии a от начала координат O. Задача 5. 3.. х-а.
Поворотный кран вращается вокруг оси, перпендикулярной плоскости фигуры, и проходит через точку О Людмила Фирмаль
Два мне угловой скорости: КП = КТ. Вдоль стрелы крана, мост Oxit перемещения тележки м с нагрузкой в соответствии с = а потому, КТ, ут = 0(рис. а). Абсолютное уравнение движения для трека Л1 «Ось ось определенного угла * горения. Прямая двухосная как относительная точка м в абсолютной координате » координатная тема Оху、 В нашей задаче х, — значение COS КТ, Г Я = 0, г = КТ Подставляя эти значения в уравнение(1), находим уравнение абсолютного движения точки M в декартовой системе координат. х = соѕ-лит、 г = а потому что КТ грех КТ.
Уравнение локуса абсолютного движения точек легче всего получить в полярной системе. р = г * * = значение COS КТ, КП = ЛЛ Откуда? р=: а потому что «эльф». Это уравнение окружности с диаметром a через начало координат O (рисунок B). Как видно из состояния задачи, время, когда точка M полностью вибрирует вдоль стрелки Oxlf, равно、 2г. Давайте найдем время Г. В течение времени Г точка M представляет собой круг диаметром a в абсолютном движении (рисунок B). £A \ 0 \ X = 2
- 0 *.Длина кривошипа g, длина шатуна AB = * 1.Ползунок B перемещается по прямой линии через точку O в направляющей. Определяет уравнение относительного перемещения ползунка B в системе координат x1, где начальная точка совпадает Места соединения рукоятки и ведущего шатуна смешаны в поступательном образе. Решение. Относительное движение шатуна АВ перпендикулярно плоскости фигуры и представляет собой поворот вокруг оси через точку А.
положение шатуна в этом движении определяется углом ty — / thuAB = ^ ABO. By теорема синуса, она выглядит так: / Грех<1> г. Откуда? Это относительное уравнение движения шатуна АВ. Чтобы получить уравнение относительного движения ползуна в、 φ. Ух = — я грех ^ = — г-грех
Достаточно представить относительные координаты x1}с точки зрения найденного угла Людмила Фирмаль
Таким образом, в задаче tidal problem сложное движение кривошипа AB разбивается на 2 простых шлифовальных движения: переносное движение-вращение с постоянной угловой скоростью вокруг центра неподвижной оси Ohu и относительное движение-неравномерное вращение кривошипа вокруг центра a движущегося Xi _y.
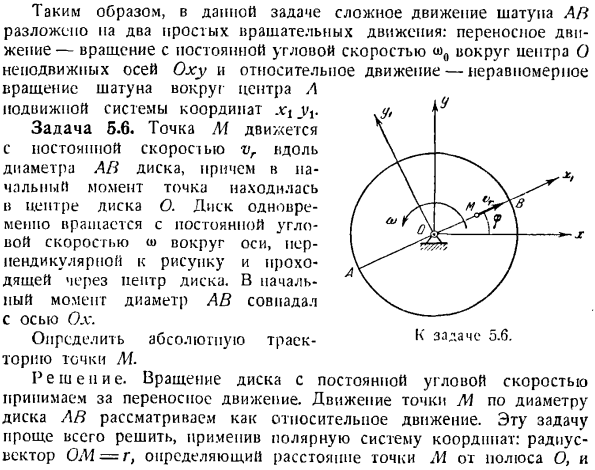
Задача 5.6.Точка м проехал с постоянной скоростью ВР вдоль диаметра АВ диска, и в первый раз было в центре диска О. диск вращается одновременно вокруг оси, перпендикулярной рисунку с постоянной угловой скоростью W и проходит через центр диска. В первый момент, диаметр АВ совпала с осью Ox. Определить абсолютную траекторию движения точки М. Решение. Вращение диска с постоянной угловой скоростью считается переносным движением. Движение точки M вдоль диаметра диска AB считается относительным движением.
Эту задачу проще всего решить, применив полярную систему координат. Радиус-вектор OM = r определяет расстояние от полюса O до точки M、 Угол г =£\хох. Это определяет угол поворота радиус-вектора, центрированного в точке O. ху = ■ Р = ври,<р = О> Т. Определите время из последнего уравнения, чтобы найти нужную траекторию Присвойте это значение первому выражению Это уравнение спирали Архимеда в полярной системе координат. Задания 5-7.Точка M совершает гармоническое колебательное движение согласно уравнению х = м, у = ЭКОСа(Т + $). (Я)
Скорость ВФ Определите траекторию, описываемую точкой L1 на экране (рисунок A). Решение. Точка м участвует в сложных движениях. Абсолютное или результирующее движение представляет собой линейное гармоническое колебательное движение точки M относительно неподвижной системы координат Ohu, определяемой Формулой(1).С другой стороны, абсолютное движение точки М мысленно раскладывается на относительное движение относительно экрана и пропорциональное движение фиг с экраном. Соотношение между координатами точки L1 в абсолютном и относительном движении выглядит следующим образом: * = + г = y0i + Йи>(2)
Где x0i> y0j-координаты начальной точки Olt относительной системы. Координаты, xyy y {искомые координаты точки M в относительном движении. Следующий Йоу! Экран осциллографа, регистрирующий движение точек G、 Перемещение влево с постоянной Н У м. 0,0. * \ В. Один.) от М до г..( б.)
К задаче 5.7. r-радиус-вектор точки M (рис. 5.1) абсолютной системы координат, rt-радиус-вектор той же j точки относительной системы координат и r0 {- радиус-вектор начала координат движущейся относительной системы координат Совместное предприятие Куда? Р = ХІ-\ — в YJ — \ — ЗК、 Р0 = х0, 1-г-У0 + ол р= х, я, — ^ yji-п-р, ФТ. В этих уравнениях x, y, z являются абсолютными координатами точек M. xQ, ya-координата начала координат системы координат относительно точки 0 {Ohu system. Формула (2) или (3) определяет уравнение абсолютного движения точки M в векторном виде.
Уравнение(5*) дает векторное уравнение движения точки в относительном движении. (3 *)(4 *)(5 *) Уравнение абсолютного движения точек получается из (2*).、(3 *)、(4 ) рассмотрим и (5), либо проектируем по оси Oxyz, либо используем формулу аналитической геометрии, связывающую координаты точек M в 2 системах координат: абсолютной и относительной: (С、*) л:= x0i-Ф, Х, ай я-й-o3r» * = «И-Ти- * я ту я-Бзи- Из (I) и(2)
, Вы можете увидеть следующее: ЮА=-vjt + значение COS(т + п) = О-Ф ут н далее Х, = ВГТ, г] = а соѕ(КТ). Исключим время из этой системы уравнений и получим уравнение орбиты относительно точки М. У1 = со.(^ + Р). Это уравнение синусоиды. Длина волны этой синусоиды (рисунок B) показана в L. 1 полное время вибрации (цикла) будет: Поэтому частота колебаний k точки M связана с длиной волны на экране следующим соотношением
. Для овладения навыками решения задач определения траектории и уравнения движения в относительном и абсолютном движении точек И. В. Мещерский из сборника задач теоретической механики к 1950 году и позднее рекомендует решать следующие задачи:417、418、419 、422、423、425。 В этих выражениях, о. каждый из них、 Оси абсолютной и относительной систем координат. Например o. I = cos(x, yx \ 7z = cos(2, z.) etc) В формуле(6) координаты xQ, yQ ^ zQ(>и Оси абсолютной и относительной систем координат известны как функция времени, когда задается переносное движение. Относительные координаты xit y \%z определяются уравнением (1) как функция времени.
Уравнение движения транспорта имеет тот же вид, что и уравнение (6), только X\, y, r, в этом случае необходимо иметь в виду 3 числа, которые определяют фиксированные координаты пера в определенной точке time. In некоторые задачи, уравнения абсолютного и относительного движения точек также могут быть получены из более простых геометрических соображений. Уравнение (I) определяет относительную траекторию движения точки M в параметрическом form. To определите относительный путь
В точке M в координатной форме необходимо исключить время из системы уравнений(1*). Поскольку координаты xQi> y0 ^ y r0j и xb yy r, а также Косинус направления aif » \ i>являются независимыми параметрами-функциями времени, формула(6 *) определяет абсолютную траекторию точки в параметрическом виде. Точка M в координатной форме должна быть исключена из уравнения (6) времени.
Если переносное движение плоское и относительное движение происходит в одной плоскости, то уравнение для абсолютного движения точки (6) упрощается. Уравнение (6), обозначаемое углом между положительным направлением оси l и xb, выражает отношение между абсолютными и относительными координатами точки、 х = ХГ. — — х] потому что а-у, грех) О, я г = zyQi — \ — х} грех Аку, потому что. Дж Кроме того, если перемещение плоскости относительно плоскости отношения является поступательным, можно выбрать относительную систему координат таким образом, чтобы ось x и ось x}}и y были параллельны. Тогда уравнение (7 *)принимает вид: х = x0r + ху г = y0i + ый(ч. *)
Если переносное движение представляет собой вращение вокруг неподвижной оси и относительное движение точки происходит в плоскости, перпендикулярной оси вращения, то начало относительной системы координат совмещается с осью вращения, а ось z совмещается с осью zh, чтобы найти уравнение абсолютного движения из (7*). Х = Х \ я-Джей-грех, грех, у = = Х {грех-\ — Г \ потому что. (9 *) Для некоторых задач используются другие системы координат (полярные, сферические, цилиндрические и др.), вы получаете более простое решение.
Задачи, связанные с этим разделом, делятся на 2 типа: 1.Относительное и относительное фиг-подобное движение точек является known. It необходимо определить уравнение абсолютного движения и абсолютную траекторию движения точки. 2.Известен абсолют и соотношение точек фиг-типа movements. It необходимо определить уравнение относительного движения и относительную траекторию движения точки.
Первая задача-суммировать движение 2 составляющих точек. 2-я задача является известной Абсолютное движение неизвестного относительного движения должно быть определено, с данным переносным движением. Такая последовательность действий рекомендуется при решении задачи. A. Если есть относительный и относительный ur-подобный movement.
It необходимо определить абсолютное движение. 1) разложить абсолютное движение точки на отношение 2 и относительное составное движение. 2) Выберите 2 системы координат: абсолютная система координат, условная и неподвижная система координат и относительная система координат. 3)составить уравнение движения точки. 4) Любой тип уравнения (6) — Используйте (9), чтобы создать уравнение для абсолютного движения точки. 5) исключить время из уравнения абсолютного движения для точки находит уравнение абсолютной траектории для точки в явном виде. B. приведены абсолютные и сдвиговые движения.
r re-bu g r s I определяет относительное движение: 1) разложить абсолютное движение точек в соотношении а и относительное 2 движения. 2) Выбрать абсолютную, условно неподвижную систему координат и относительную систему осей. 3) Создайте уравнение для абсолютного движения точки. 4) Найти уравнение относительного движения точки, используя уравнение любого типа(6)- (9). 5) если исключить время из уравнения относительного движения точки, то вы найдете уравнение относительной траектории точки в явном виде. Задача 6.1.Корабль плывет вниз по течению.
Скорость движения по реке 2 м \с. Скорость движения судна относительно неподвижной точки составляет 10 м/с. Создайте уравнения для относительного и абсолютного движения кровеносных сосудов. Разрешение: выберем относительную систему координат и начало абсолютной системы координат в точке, где судно находилось в первый момент. Мы воспринимаем поток воды как подвижное движение. Поскольку относительной системой координат является система координат с движущейся водой, то она участвует в движении подвижного объекта со скоростью 2 м / s.
To составьте уравнение относительного движения судов, мысленно остановите течение реки. Тогда легко получить уравнение относительного движения Джиф! = 10 т. Абсолютное движение корабля — это движение относительно берега, система координат, плотно связанная с землей. Уравнение абсолютного движения в этом случае выглядит так: Х = Х {+ Х «、
Где jc * — абсцисса начала координат системы координат относительно неподвижного берега. Временная зависимость абсцисс x2 определяется уравнением. Си = 1Т、 Таким образом, уравнение абсолютного движения кровеносных сосудов имеет вид х = 10и-1-2 / −112 нет. Задача 5. 2.Кривошип OA, согласно формуле cp = M, равномерно вращается вокруг неподвижной точки O в плоскости фигуры. Длина кривошипа и шатуна равна, OL = LV = r. ползуны перемещаются в направляющей вдоль осей Ox.
ПАЗ прочно прикреплен к ползунку и перемещается постепенно как 1 твердое тело вместе с slider. In ПАЗ, точка M перемещается так, что расстояние составляет 0 \ M = rsmkt. Определите относительное движение точки M и уравнение абсолютного движения, а также ее абсолютную траекторию, предполагая движение точки movement1 относительно относительного положения канавки. The solution. By выбор вокруг относительных координатных осей OxX \ Y \
Найти уравнение относительного движения точки M {0}, как показано на рисунке. Х [= 0,г)= р грех КТ. г. м. икс Так… К задаче 5.2. Отношение рис-подобное движение будет трансляционной точкой nepeeb вместе с канавкой. Поскольку переносной ДК представляет собой плоское поступательное движение, уравнение абсолютного движения м можно получить из системы(8*).След. ’Песня абсолютного движения х = x0Jrxl, у = У0-\ — стеллаж для просушки Где x0, yQ-текущие координаты системы координат. Поскольку это OL = AB, определите координаты. Проследить< ХЖ = ОА коф Подобный этому
Смотрите также:
Предмет теоретическая механика

