Оглавление:



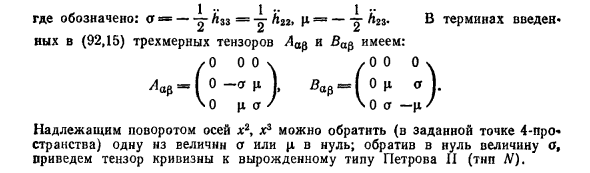

Слабые гравитационные волны
- Слабые гравитационные волны. Конечность скорости распространения взаимодействия Подобно электроду, направляй релятивистскую теорию гравитации Намику, к возможности быть не связанным с телом Свободное гравитационное поле-гравитационные волны.
Глядя на слабое свободное гравитационное поле в пустоте. Введем тензор / ^, описывающий слабое возмущение, как в §105 Галилео показатели: gik = gik) + hik • (107,1) Кроме того, до основного количества ч ^ к Инвариантный метрический тензор: gik = gik (0) _ hik ^ (1 0 7 2) И определитель тензора g ^: g = g (°) (l + / 0, (10.7.3) Где h = h \\ все операции, которые поднимают и понижают тензоры (0)
состояние малости остается Возможно любое преобразование справочной системы форма Людмила Фирмаль
Индекс генерируется невозмущенной метрикой g-k. Как уже упоминалось в § 105, x, r = xg + smallg, одновременно = ** — H-W- (107’4) Используйте это будет в калибровке (как говорится В связи с этим) дополнительный тензор / ^ тон g j = 0, fc = hik-h f h, (107,5)
После этого тензор Гиччи находится в простой форме (105.11). Rik = \ n h ik, (107,6) Где □ представляет оператор Даламбера. □ = 0) _d__ = d _ 1 8_ ёdh1dht c2 dt2 * Условие (107.5) все еще не фиксирует четкий выбор Опорная рамка: когда некоторые из этих условий выполнены Отверстие, и только если они также заполняют (107.4) Решение уравнения □ f = 0. (107,7)
- Если уравнять уравнение (107.6) до нуля: Уравнение гравитационного поля в пустоте в пене □ L * = 0. (107,8) Это нормальное волновое уравнение. Следовательно, гравитация Как и электромагнитное поле, ононное поле распространяется в Сторт со скоростью света. Рассмотрим плоскую гравитационную волну.
В такой волне Поле изменяется только в одном направлении в пространстве. Выберите ось x 1 = x в качестве этого направления. равных Будет уравнение (107.8) (Я? — ???!) ‘*? -0 ‘<107-9> Решение является произвольной функцией от t = b x / s (§ 47). Распространять волны в положительном направлении ось XII. Значение hk в нем есть все функции т-х / с.
точка над буквой означает различие К Людмила Фирмаль
Дополнительные условия в этом случае (107.5) -u = 0, т. Эти равенства можно интегрировать, просто удалив их Дифференцирующий символ; интегральная константа Я заинтересован здесь (как ноль) (Для электромагнитных волн) это просто переменная часть поля.
Поэтому между отдельными компонентами Ratio: Φ1 = Φ1, Φ1 = ΦbΦ1 = ΦoF s =, Φ0 Как показано, условие (107.5) еще не определено Справочная система, координаты могут быть опубликованы x, r = xr + ({t-x / c) преобразование формата. Это преобразование Может использоваться для 4 недействительных Количество: от ф®, ф®, + ‘0з * равенство (107.10)
В этом случае компонент φ \, φ> Φ3 также исчезнет. Оставшееся количество В этих преобразованиях (107.4) ^ = Јi (t-x / s) для этих компонентов исчезают при выборе системы отсчета Не меняйте это вообще. Обратите внимание, что оно исчезает и φ = φ%. Следовательно, fk = hk.
Поэтому плоские гравитационные волны определяются Две величины: / 123, ^ 22 = -Л33. Другими словами, гравитационные волны — это поперечные волны, поляризованные волны. Его положение определяется симметричным тензором ранга 2 Сумма плоскости yz и диагонали / 122 + ^ zz Равно нулю В качестве двух независимых поляризаций вы можете: Выберите, если одно из двух значений не равно нулю L-23 и (^ 22-Lzz) / 2.
Эти две поляризации отличаются друг от друга. Друг друга, вращая под углом 7g / 4 в плоскости YZ. Рассчитать псевдотензор энергии импульса плоского гравия Национальная волна. ТЛК компонент является вторичным количеством Маленькие, должны игнорировать участников и вычислять их Высший порядок.
Если h = 0, определитель g = -1 отличается только вторичным количеством, тогда В общей формуле (96.9) ее можно записать в виде Qlk, i ~ glk, i ~ -hlk, i. Для плоских волн все ненулевые члены в tlk заключены Для членов (96,9) в фигурных скобках (это Одна из осей системы отсчета Galileo в направлении распространения Блуждающие волны).
Вот так tik = ^ h y h q’k. (107.11) 32 тг до q p V} Поток энергии волны определяется величиной -cgt0a ~. «Ct0a. В плоской волне, распространяющейся вдоль оси x1, Зависит только от ненулевого L23 и L22 = -L33 Разница t-x / s, этот поток направлен вдоль одной оси x1, равных Для 167G hlz + \ {h22- h zzf \. (107.12)
Начальные условия для любого гравитационного поля Волны должны быть определены с четырьмя произвольными функциями Координаты: из-за боковой природы волны, есть только два независимых компонента, их необходимо указать Также первая производная.
Этот счет Создано здесь на основе характеристик слабой гравитации Поле, но в результате — число 4 — явно не подключается Занято это предположение, относится ко всему бесплатному, Другими словами, гравитационный мю поле.
Оспаривать Определяет тензор кривизны для слабых плоских гравитационных волн. Решения. Если вы вычислите повторное число по формуле (105.8), вы увидите следующее. Ненулевые компоненты: — # 0 2 0 2 = # 0 3 0 3 = — # 1 2 1 2 = # 0 2 1 2 = # 0 3 3 1 = # 3 1 3 1 = <7, # 0 2 0 3 = — # 1 2 3 1 = — # 0 3 1 2 = # 0 2 3 1 = M, а = — ~ ^ sz = № = — ~ ^ 2 с- (92.17) 3D-тензоры Аар и Вар, / 0 0 0 \ / 0 0 0> Aar = 0-a II, Var O II a \ 0 / l a J \ 0 a-fi)
Вы можете изменить направление вращения осей x2 и x3 (в определенной точке) 4 пробела) количество а или (от 1 до 0; исчезновение количества) Теперь приведем ср и тензор кривизны к вырожденному типу Петрова II (тип N).
Смотрите также:
| Гравитационное поле вдали от тел | Гравитационные волны в искривленном пространстве-времени |
| Уравнения движения системы тел во втором приближении | Сильная гравитационная волна |

