Скорости точек плоской фигуры

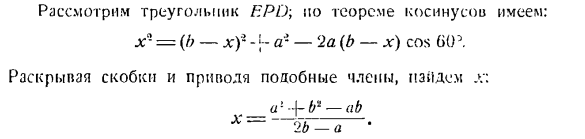
Скорости точек плоской фигуры

• Скорость точки плоской фигуры Скорость точки На виде в плане может быть определена безболезненным методом, графическим методом или графическим анализом method. In в этом разделе вы рассмотрите определение скорости движения точек на виде в плане с помощью аналитических приемов и графоаналитических приемов.

Анализ method. In аналитическим методом, необходимо дать уравнение позиционирования поэтажного плана (рисунок 6.3） (1 *） SP(3 *） = А(О » ПО2 = А(0. 9 = А (О- Проекция координат скорости точки At на фиксированные координаты определяется уравнением. 1> x = * o1X-(* LU-J’o、） » в VY = v0 в, г-р(х-хо} В этих уравнениях vK} vy-искомая проекция скорости точки в фиксированной координате osp.

Графический метод определения скорости точки состоит из составления плана скорости и рассматривается отдельно. Людмила Фирмаль

v0tX = x0, v0 y = V0-проекция Положение центра мгновенной скорости также может быть определено аналитически. На тему стационарного положения оси координаты мгновенного Центра определяются по формуле: хр-хо {^. УР-во, (id） В этих уравнениях xp, ur являются мгновенным центром скорости и координатами фиксированных сносок. xa> y0i-координата полюса.

Начало системы подвижных осей; v0t, v0 ^ v-проекция полярной скорости на неподвижную координатную ось. — Проекция угловой скорости фигуры от оси, перпендикулярной плоскости, в которой происходит движение occurs. In подвижная система цапфы, она более твердо соединена На виде в плане координаты центра мгновенной скорости являются ВН Р Сино-тфн о потому что 0,1-04 *） (15 *） * В..)rcos <Р + волв грех? Здесь. * ^ ip » J’ip-ось psd-координаты центра мгновенной скорости в системе pajpo. 6-угол поворота подвижной системы координат относительно остальных.

• Оставшееся количество совпадает с WH и k (13*). Выражение（13 *）»（14 *）、（15 *）рекомендуется использовать приведенное уравнение движения (1) плоской фшуры. Если скорость известна по условиям или можно без особых затруднений составить уравнение движения (1) вида в плане, то рекомендуется использовать аналитический метод для определения speed.

In в целом, аналитический метод позволяет найти скорость точек на виде в плане как функцию времени. Однако не всегда удается получить такое решение в обозримом формате. С помощью аналитического метода рекомендуется решать задачу в следующем порядке: 1) Выберите фиксированную и перемещенную систему координат. Начало системы движения осей также может быть взято таким ярмом, уравнения движения которого известны или могут быть составлены без особого труда. 42) построить уравнение движения в плане: уравнение движения полюсов 2 и уравнение вращения фшура вокруг полюсов.

Рекомендуется использовать метод графического анализа для определения скорости точек плоской фигуры, когда необходимо найти скорость различных точек плоской фшуры в определенное время в определенном положении плоской фшуры. Людмила Фирмаль

 3)используя уравнение движения плана, получим 1 уравнение движения точки, в которой нужно найти скорость. А) определить проекцию скорости па неподвижной или движущейся оси координат, найти величину и направление искомой скорости.

В этом случае, если необходимо определить скорость нескольких точек, то решение задачи с использованием центра мгновенной скорости является более эффективным, чем другие методы анализа графов, а мгновенный радиус можно вычислить без сложных вычислений. Если скорость одной точки На виде в плане требуется в соответствии с условием задачи, то целью обычно является теорема распределения скорости (9*) или теорема о том, равна ли проекция скорости в конце сегмента на виде в плане направлению самого сегмента.

Для решения задачи методами графического анализа рекомендуется выполнить следующие действия: 1) Выберите точку на виде в плане на полюсе, скорость которой известна или легко определяется из состояния задачи 2) Nygm d.) первая точка на виде в плане, где известно направление скорости. 3) используйте формулу распределения скорости, чтобы найти скорость этой точки На виде в плане. 4) определить значение угловой скорости плоской фигуры в заданный момент времени на основе формулы распределения скоростей. 

5) если известны угловая скорость фигуры и скорость полюса, используйте формулу распределения скоростей, чтобы найти искомую скорость других точек фигуры. Если вы используете графический способ решения проблемы, вы также можете применить проекцию method. In в этом случае мы рекомендуем выполнить следующие действия для решения проблемы. 1)Выберите точку в плане полюса, скорость которого известна.

 2) используйте формулу распределения скорости для построения скорости другой точки На виде в плане, где направление скорости известно. 3) скорость результата в направлении линии, соединяющей обе точки, спроектировать треугольник и найти скорость 2-й точки. 4) Скорость проецирования треугольника в направлении, перпендикулярном прямой, соединяющей обе точки, найти скорость вращения 2-й точки относительно полюса. 5) разделить скорость вращения на расстояние до полюса (точка og) и найти мгновенную угловую скорость плоскости

в) если вы знаете мгновенную угловую скорость фигуры, вы можете использовать формулу распределения скорости, чтобы найти скорость любой точки плоской фигуры. Если задача решается с помощью мгновенного центра скорости, то рекомендуется следующая последовательность действий: 1) определить положение мгновенного центра плоской фигуры с помощью одного из приведенных выше способов. 

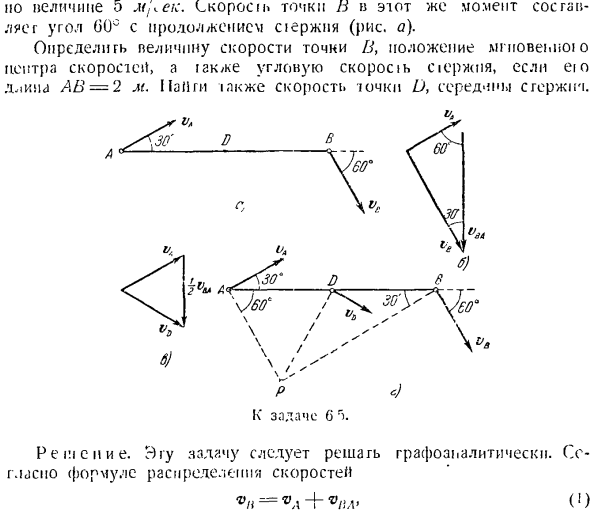
2) найти мгновенное значение радиуса точки, скорость которой является известной плоской фигурой, и определить угловую скорость плоской фигуры, разделив скорость точки на мгновенное значение радиуса. 3) найти искомое значение скорости точки плоской фигуры, используя формулу (11*), умножив мгновенный радиус точки, соответствующий угловой скорости. Задача 6.5.Стержень АВ совершает плоское движение. Скорость точки А равна току, образуя со стержнем угол 30° Но про Мрэик это важно.

Непосредственную точку и, в тот же момент, сделать продолжение оси и угол 60°(рисунок а). Определить величину скорости точки B, мгновенное положение центра скорости, а также угловую скорость в случае AB = 2 м, а также найти скорость точки U, являющейся серединой стержня. «ВВ 7> в моем Jeo^«\ / ^✓ ’\ ва. 30. Д. 30. 6.） \ ’ К * проблема 6р). Решение. Эта задача должна быть решена графически. Согласно формуле распределения скорости = + О (I) на 3-х скоростных феуголках соответственно. Па любой юбке был выбран 01klayyipgsm.

масгигабс Н быстро. Vv известен, но величина и направление являются прямыми, параллельными, прямая линия * ОНА, T, от конца va. Перпендикулярно стержню вектор v! Размер ИА неизвестен. Использует направление скорости vn. От начала вектора vA, направление r! Направление до пересечения с v! Нарисуйте линию, параллельную T. 

In таким образом, получается замкнутая «направляющая скорости», а сторона выбранной высоты шкалы определяет скорость вращения точки B вокруг крайней точки B и Полюса A. Если вы решите треугольник, вы можете увидеть следующее: (2） IC = vA(g 60° = Г) KZ 8, (55 м / с ck; vBA = — «ZM =о» •2、 Я заметила. Из (2) и (3) определите значение угловой скорости. a> * 2 = 10 или 10 = 5 секунд. Скорость изгиба D в центре стержня an можно найти по формуле распределения * D = VA’B2 VHA- Построить треугольник скорости из любого стержня (рисунок C), чтобы обеспечить скорость vA.

Отложите вектор из кучи vA、 Равный -} Ивна. Соедините начало вектора vA и конец вектора-j VL. Найти нужную скорость в точке D. Скорость точки D можно легко определить по треугольнику скоростей. Размер нижней стороны этого треугольника vA равен- =) вна = о AtjccK » и угол между этими сторонами (Ил. Эта проблема также может быть решена немедленно с помощью мгновенного Центра.

Мгновенная скорость стержня, чтобы найти центр, нос 13IHIM перпендикулярна скорости точек A и H(рисунок D).Пересечение этих прямых линий определяет расположение центра нескоростного Центра R. In прямоугольный треугольник ANR, мы знаем сторону AN и 2 смежных угла: HAP = 60 \ / TABP = 30°. Найдите мгновенный радиус AP и HP. АП = ах греха 30°= 2-0. 5 = 1 м, HP-an cos 30°= 2*, y ^ 1,73 м Величина угловой скорости стержня VA 5.—、 ВТ = ЛР = Г=°’

Следовательно, величина скорости точки B вю.= ^ 5•1.73 = 8、（）0 м / с. пропол Ми понсии и радиус PD определяют скорость движения центральной точки D стержня. ИГ: следовал треугольник ЛОР. AP= xsAl)= 1 l *. таким образом, треугольник является равносторонним, а DP = I m. L или да vr, — = DP•<o = 5 м / с. Скорость точки U ориентирована перпендикулярно мгновенному радиусу DP. Для этой задачи оба решения эквивалентны. Точно так же можно быстро получить ответы на все вопросы, поставленные в задании.

Если необходимо найти величину скорости точек, то проще всего применить теорему к уравнению проекции скорости 2 точек в направлении вида в плане отрезков, соединяющих эти точки. ва соѕ 30°= — в [} cos60e、 Откуда? В. Косенко. 1 / О «’ Г°_ О ^ К в. l = = мнэз-8, (35 м! Считанные секунды.- Задача 6.6.Кривошипный механизм состоит из кривошипа OA и кривошипа AB такой же длины, и кривошип вращает вокруг фикчированного центра O. 

Один. К проблеме(Ш Скорость полюсов, начало движения системы координат x ^ yx по фиксированной координатной оси. to,= = £ — проекция угловой скорости на ось 2, перпендикулярную плоскости движения. x, y-координаты точки M в фиксированной системе координат. X°C-координаты полюсов O в осевой системе. Координаты x, y точки M определяются уравнением движения (12) в плоской форме (1) с использованием формул, приведенных в этой главе. проекция скорости точки На па Один Координаты определяются по формуле: Р \ = v0 в, Х что? Грех? — Рисунок 6.3 (4*) (5 *）%=- v0iX грех с? + v0iy cos i-f UgXi. В этих формулах vXl, vVl-искомые проекции скорости точки A1 на ось x} 1

Формула 9 =шарнирно соединенный шатун L в центре колеса. Колеса с радиусом крен горизонтально без скольжения!） Найти уравнение движения для плоского движения колеса и уравнение движения для точки распада Л1.Точка коллапса L1 находится в контакте с плоскостью, когда точка B находится в крайнем положении.

Определяет скорость точки М и мгновенную угловую скорость колеса. Решение. Нерв methods. At крайнее моральное положение точки B, выберите начальную точку системы координат без движения (рисунок B). ось X направлена горизонтально влево, а ось Y направлена вертикально вниз. Выберите точку B в качестве полюса. Создайте уравнение движения для полюсов. хп = ’ 2г-2г, потому что КТ = 2р(я-потому что / с /),(т） Уу = ^(2） 3-е уравнение движения, чтобы получить временную зависимость угла поворота, колесо катится без скольжения, поэтому смещение центра колеса в точке B можно выразить как угол поворота колеса

Определите скорость вращения 4 точек на ободе цилиндра на концах взаимно перпендикулярных диаметров, указанных на чертеже. Решение. Центр покрывала скорости цилиндра Mi на пункте D, где фикчированная часть нити HD В контакте с cylinder. In у этой мины точки соприкосновения между точками Шины и цилиндра равны, а значит, равны и пуле. Оставшаяся скорость //// год’//////、

Проверьте пропорционально Стоя в центре мгновенной скорости, перпендикулярно мгновенному радиусу. Скорость точки 11 определяется из соотношения Р ~~ ИК ’ т.） Оттуда, учитывая(1)、% = — 4rT»5au. (2） Цель G. 8. Направление скорости в точке Е перпендикулярно мгновенному радиусу. Dfz, Т. С. Параллельно точке L скорость. Скорость точки C / / равна по величине, так как она отделена от мини-центра Скорость, точки равноудаленные Дpa DC = DH = r \ ’ 4 * значение этих скоростей определяется из соотношения Так… Где я? ви:= вю:= — \ логии; (3）

Скорость Эгера направлена перпендикулярно мгновенному радиусу SP и HD (для рисунка). Уравнения (2) и (3) определяют скорость точек C,£, / 7 как функцию расстояния y, от которого смещается центр диска. Найти величину этих скоростей как функцию времени. В задаче 0.7 на основе теории (1) были выведены уравнения движения центра диска. Подставляя это значение расстояния y В Формулы (2) и (3), получаем: н. Цель G. 9. 4. Величина скорости точек C и / 7 также может быть найдена на основании теоремы о равенстве проекций на линию, соединяющую эти точки скорости из 2 точек плана этажа.

Скорость точек C и H находится под углом 45°к линии SAN, а скорость точки A направлена вдоль этой линии line. So … ВК в COS 45°=©, соз 45°= в> Откуда? г 2 | / 2, / л- * 2,—2/2 ″ Задача 6.9. Стержень скользит горизонтально в точке А jc касается круга радиуса r все время, с половиной вдоль оси Определите угловую скорость стержня AN, если скорость в точке A равна vA. П е и Е в нем. Если обозначить угол между стержнем AN и осью l буквой_. * = VII в + в} = Ввит «Г» Цзи-(г> ’）

Направляющий Косинус задается уравнением： потому что(vTx)= іх, потому что(в})= УУ,(и 7J） потому что(в? х {)= п>\, потому что(по!=?У1. (8 *） G A f a i A l A i N h e s K P E метод s. I первый метод анализа графа, который определяет скорость точки На плоской фигуре, основан на уравнении распределения скорости(рис. 6.4） «=Р „0i-ж-м> х „ручьи“. (9 *） В этой формуле v-желаемая скорость точки At. v0-скорость полюса 0-это угловая скорость в плане этажа. G и радиуса-вектора от полюса 01 м. от g до X-координаты (I) точки A, которая дифференцируется по времени, следующие: сделать R Fi интернет \■ (H d.\Or, учитывая• ’ — u) r, — (=vA, находим： х-потому что (iH0 — -<р) л — “ АК х Ту же проблему можно решить и другим способом.

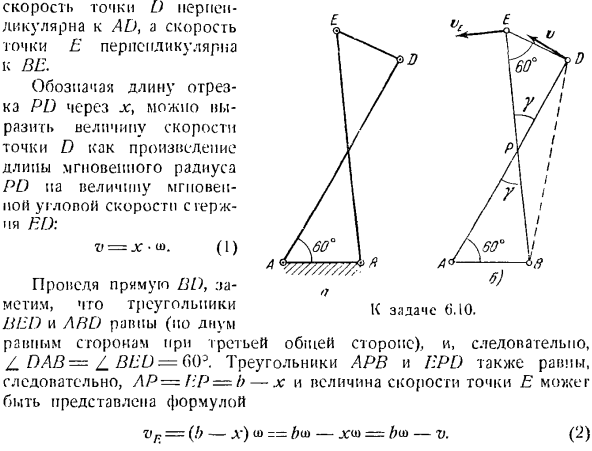
Скорость точки K направлена по касательной к окружности, то есть вдоль стержня LI. скорость точки A равна сумме скоростей полюса, чтобы принять скорость вращения вокруг точки K>и Полюса. Куда? Спроецируйте геометрическое уравнение (2) перпендикулярно AB\ vA sin-f=») и K, учитывая угол, где? Увеличивать v Син(ов. г (О-4 — л АК Х \ .’- ХТ-ГУ Задача 6. 10.Шарнирный прямоугольник ABED (рисунок A) (AB-EI) — a> AD = BE = b имеет неподвижную связь AB.

Скорость точки D известна и равна gk Определить скорость точки Е и мгновенную угловую скорость звена Эд, если в данный момент угол составляет DAB = 60°. Решение. Мгновенный центр скорости звена Эд расположен на пересечении стержней BE и AD, в точке P (рисунок B). Скорость точки перпендикулярна AD, а скорость точки E «l-v перпендикулярна IJ ^ k. вы можете сделать следующее: * 1 — \/\/Я показываю длину поножей ke X из PD, можно -\ / \ y / /

Добавить значение скорости/ / \ / 1 В ПУ /в качестве продукта из точки D Длина мгновенного радиуса/ 1/! Значение PD петь угловой скорости в gerzh ~ / \ / \ 1 Ния Ред:/ \ / 1 / В = Х-У>. (Я) Ф \ 60 * 1 ] И Я… * —1-1> <9 — TJ J / нарисуйте прямую линию BDf Треугольник 1С (спина) j. io обратите внимание, что (. Кровать и LAN) равны (но 2 3-я общая плоскость и равная плоскость), следовательно, DAB-BED = GO3.Поскольку APB и EPD треугольника также равны, AP = IiP-b-x, а скорость точки E можно представить формулой: (2） ВФ =(б-н») у)= ФМ-. Рассмотрим треугольник полиции. Но есть косинусная теорема: x — =(b-xf—(2a (b-x) cos G0 \ Разверните скобки, чтобы процитировать похожие термины и перейдите к> :: —А * + Р-АБ Х ~ ~ ’ф а’

Здесь можно определить значение мгновенной угловой скорости стержня по Формуле (1) га） в б. а. (О- — — В — • — Д. х—ло-АБ 7’г.： Подставляя это значение в выражение (2), получаем: Ф 2lr-АБот J \ г_ _ о ’ Гамма:(р-р б-Ио 1; в <р-и-о—■б Эго-это искомая скорость точек/.в этом положении механизма. Задание 6.11. Жесткая прямоугольная вершина а паа (рис. а) соединена с неподвижной точкой О.

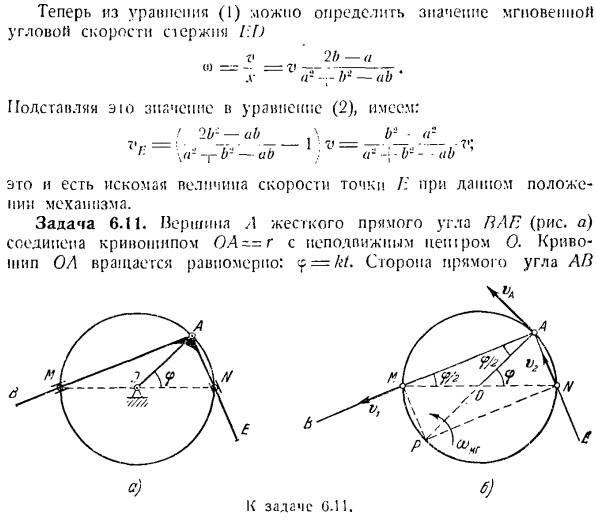
кривошипом ОА〜= R. кривошип ОА вращается равномерно: — f = kt. Прямоугольная сторона AB 0. б.） Проблема Г. 11.Для. Проходит непрерывно через неподвижную точку M, а стержень AB проходит через неподвижную точку N. И N находится на окружности, описываемой вершиной прямого угла A. Определяет угловую скорость твердого тела, углы прямоугольного бала и скорости тех точек, которые в данный момент соответствуют баллпиа i \и N. Решение.

Плоское движение стержня AB можно разбить на 2 простых движения: поступательное движение вдоль стержня AB и вращение стержня вокруг шарнира M. следовательно, скорость любой точки на стержне будет состоять из компонентов d-ivx. ; Величина скорости вращения пропорциональна расстоянию от точки до шарнира M. So, в точке стержня, которая в данный момент совпадает с шарниром м, составляющая скорости вращения пули равна скорости, скорость которой направлена вдоль стержня АВ. Аналогичным образом, мы приходим к выводу, что скорость точки стержня AB, которая в настоящее время совпадает с точкой N, ориентирована вдоль стержня A/:.

Восстановим вертикальную линию относительно направления скорости ярма стержня, которая совпадает с М и L/.Точка пересечения этих перпендикуляров P находится на окружности AMN и является мгновенным центром перпендикулярной скорости PAE. Точка P находится на окружности! И потому, что ohj является вершиной прямого угла MP MPN, который поддерживается диаметром круга. Значение коэффициента принадлежности кривошипа ОА и модуля упругости точки А、 ва = ОА — \ з \ = РК. (Я）

Величина скорости той же точки A, которая принадлежит прямому углу BAE, равна произведению мгновенной угловой скорости угла Yugo и мгновенного радиуса AP. ва = АП. гайка = 2р«4Р(2） Получим значения мгновенной угловой скорости в плане A BII из уравнений (1) и (2). = = константа Скорость точки стержня AB, совпадающей с шарниром M, равна величине произведения мгновенной скорости выхода pa и мгновенного радиуса MP. в {=МП *% Р-2р грех * = ру грех (Угол AoM равнобедренного треугольника с n в основании AM равен s / 2, потому что сумма должна быть равна внешнему углу C).

Шарнир N соответствует скорости точки AN «О Л О r = D’P * yMH = .- r 2 g cos•= r к cos. Как показано на рисунке, направление скорости заострено точкой A n, проходящей через L /и в данный момент проходящей через L’. 6. Задание 6.12.Неподвижное звено A / 3 = 1, кривошип AD = o, BH = b и 4 звезды PNC(рисунок O) шарнирный шарнир Li =(соединен шарниром. Кривошип вращается с постоянной угловой скоростью. Крюк] D перемещается по дуге между двумя крайними положениями (рис. c и d).

Определить а02 угля АББ,<С01.< Tl, образуя прямой кривошип AB в крайнем положении. Здравствуйте, угловая скорость AD. The solution. At первое положение, углы = /- а потому, что 7.0.,, — (д-б) поле грех= грех Где я могу его достать： Сои. −1′ + Соя r0-2—•> //// _ 1、\ » Я * — {Д-Б)* — \ — а * потому что a0j= — — -^ -!- Приступаем к определению угловой скорости кривошипа ад. с)д） К выпуску 6.12. (Диаграмма b). Нарисуйте прямую линию с\, длина которой обозначается k. прямая AB имеет угол наклона a. А = А, — и-хз.

Та же линия, образующая угол с кривошипа и угловой со ссылкой на ди. в y обозначает угол ADE, а в букве 8 обозначает направление скорости точки P i /A продолжения прямой DE. Поэтому мы выбираем это ярмо на полюсе, потому что знаем скорость точки плоской фигуры. Затем откладываем от точки А1, где скорость не определена. Шаг yur равен самому быстрому из полюсов, вектор X направлен перпендикулярно g, величина равна югу. Вектор Paya сумма этих членов приносит желаемую скорость точки Л1.

Если точка A \быстро поднимается в направлении, то можно не потерять значение поворота. Скорость (Х так как эго и 11 Скорость точки L1 и целевая скорость определяются пересечением линии, совпадающей с направлением скоростной трассы L1, проведенной из Ai, и линии, перпендикулярной линии 0 \ M, проведенной из Koosima в точке A1 к вектору V. треулюйик или параллелограмм, после того как построен первый, задача может быть решена. Отличный.

Тогда скорость точки D и/: bud> r： ВН = \ ^® а, ВФ = Где w-желаемая скорость намокания для кривошипа AD. Мы проецируем направления скоростей D и B, а также прямые линии UB, и мы приравниваем эти проекции sin f = > > coso, общая скорость цели будет: Б потому что 6 / 1П 03. = — — — — — О). (Я） Милый. Для нахождения углов b и 7, входящих в формулу (I), сначала воспользуемся косинусной теоремой треугольника ABB. k = V’B + b * — 2lbcos>? (2） из треугольника ADB, используя теорему Косинуса, используя значение r к…] — д-а * потому что?2 = i —. (3）

Однако далее, по теореме синусов из треугольника АББ: Грех 3, _ _ порог 9 ’Я’ ~~~ ~ Ф ~ ~ ~ К-9 Где я? грех фут = — фут-Н(4） ADI приводит к синусоиде теоремы колготок: paeencniy Грех 7 _ _ грех 3> Откуда? Грех 7 — = н(о） Далее, узнайте,* 8 = е-1-п −90° Следовательно、 потому что = сни(п + ФК). (си） Если ввести значения (6) и (5) в Формулу (1), то: БК НН (- 1,4-е) со,= -.— Джей-л-! (О. 1 У-Син с Зависимость от сердца Р и Р ВГ; 1А? Определяется уравнениями (2), (3) и (4), полученными ранее.

Для того чтобы получить запас быстро и легко решить поставленную задачу, можно решить следующие задачи: «Сборник задач теоретической механики* И. В. Мещерский, 19г публикации) 0 или более поздние：502、503、504、508、510、511、513、517、521、530、539。 Где vl} — желаемая скорость для точки B.\ vA — io. известная скорость точки А выбирается как ТЮС.  / м = < х / я = Вт / м(о ***） — План I.

скорость вращения вокруг точек А и А, которые равны по абсолютной величине произведению мгновенной угловой скорости а, представляет собой расстояние от точки до полюса, перпендикулярное прямой части и направленное в сторону мгновенного вращения фигуры. Многие задачи могут быть решены с помощью теоремы о равенстве проекций в направлении отрезка скорости конца отрезка плана этажа (рис.6.4). Второй! Метод парайто Ла ФАО для определения скорости точки в плоской фигуры основан на использовании мгновенного центра скоростей этой фигуры.

В плоском движении guzpah круглосуточной стойкой регистрации В любой данный момент в теле (yL 0) есть точка, в которой скорость равна нулю. Эта точка называется центром мгновенной скорости и обычно обозначается через P. единственным исключением является случай Ti’K, который называется мгновенным поступательным движением (10 = 0), которое учитывается отдельно.

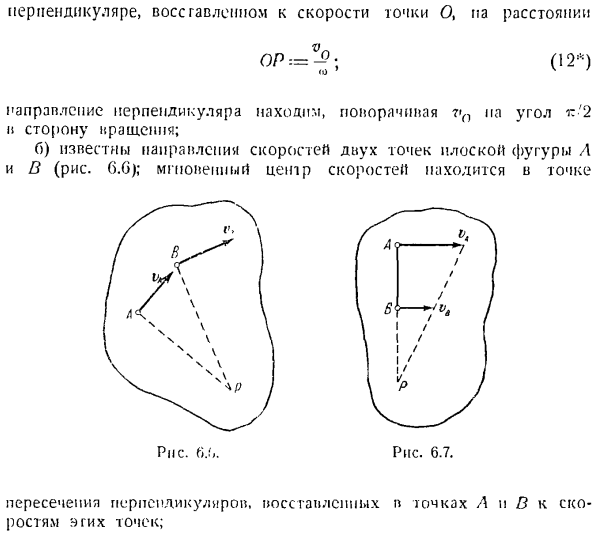
Существует закон, что если выбрать мгновенный центр полюсом, то скорость будет распределена по плоской фигуре. Рисунок.><:>. ^®=^®— (1С *） (И «） И.) «л » л __ ВР-АР〜 Как найти положение центра мгновенной скорости： а) известны скорость в 1 точке O и угловая скорость вида в плане(Рис. 0.5 J; мгновенный центр скорости равен Где v-искомая скорость для любой точки f. co-мысленная скорость плоской фигуры. g j — радиус-вектор от мгновенного центра скорости до точки M, называемый мгновенным радиусом.

Таким образом, скорость всех точек на плоской фигуре теперь мгновенна, скорость вращения вокруг центра. Эти значения равны произведению угловой скорости на мгновенный радиус, коэффициент ПА, который направлен перпендикулярно мгновенному радиусу. Поэтому величина скорости точки На виде в плане пропорциональна величине радиуса радиуса. Перпендикулярно скорости точки O на расстоянии (12 ）

найти направление перпендикуляра, вращая vn pa в направлении угла поворота t’2. b) направление 2-точечной скорости плоских валов A и B известно(рисунок G. G).Мгновенный центр скорости В точках L p на пересечении перпендикуляров, которые поднялись до скорости этих точек. в) скорости 2 точки А и в на виде в плане параллельны друг другу, перпендикулярны отрезку АВ, обращены в обе стороны и не травмированы.

Мгновенный центр находится на расширении АВ со стороны Ючи, скорость которого медленная. Расстояние от точки до мгновенного центра скорости пропорционально скорости point. To определив центр мгновенной скорости, нужно знать не только направление, но и величину скоростей точек А и в (рис.6.7). г) скорости 2 точек А и в на виде в плане параллельны друг другу, перпендикулярны отрезку АВ и направлены в разные стороны.

Центр скорости момента находится на отрезке AB, который делит этот отрезок К частям пропорциональным к speed. To найдя центр мгновенной скорости, нужно знать как величину, так и направление скорости обеих точек (рис.6.8). Рисунок Т).8. д)плоская фигура катится без скольжения по неподвижной кривой(рис. 6.9).Мгновенный центр скорости I находится в точке контакта между фигурой и кривой.

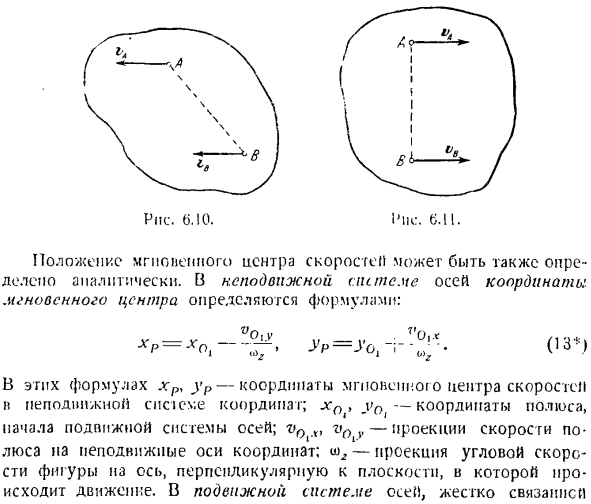
Если скорость 2 точек в плане параллельна друг другу и не перпендикулярна отрезку линии, соединяющей обе точки (рис. 10), или если скорость 2 точек на рисунке параллельна, то они равны Если они перпендикулярны отрезкам, соединяющим друг друга и соединяющим точки(рис. 6.11), то можно сказать, что в этот момент нет мгновенной неигры скорости или бесконечности. Угловая скорость

Смотрите также:

Предмет теоретическая механика

Кинематика колебаний	Подвижная и неподвижная центроиды
Уравнения плоского движения твердого тела. Уравнения движения точки плоской фигуры	Ускорение точек плоской фигуры