Оглавление:











Скорости и ускорения точек в системах криволинейных координат
- Задача 14. 7. Определяет проекцию скорости и ускорения на оси сферических координат. Вопрос 14. 1, были определены координатные линии сферической системы координат. Используя формулу 6, находим разность дуги координатной линии, а затем проекцию скорости на ось сферической системы координат ДС р д-р, ДС г р-йй, ДС Р грех 9 дип 1. И так оно и есть. Р е Ф6, rz1pe. Е 2 Здесь, роль обобщенных координат играют сферические координаты я Р ы 3 Тогда формула. 6 Найти коэффициент хромоты Я, 1, Р Э Р, З Р rsln0. 4 Поскольку нам известны эти коэффициенты, мы ищем проекцию ускорения на ось сферических координат, используя формулу 8. Г — — г Г1 rsini.
Формула 7 г-РС rsin-М1 ыя е Г1 М —, е в 7 С Г24, Л 1 г20 2гМ — rasine-cosfi-Ф2 да, dtda ea f ss — rsin0, 2z i, sine 2rcose-0 — l 8 и позже г-р -. In-o. F. , r. 1. П 2,. 1. В. Ф 2ra грех 0 потому что 6 ФЛ ф 0. Задача 14. 8. Определить проекцию скорости и ускорения точек на оси тороидальной системы координат см. Рисунок в вопросе 14. 4. Решение. Поверните линию o a вокруг точки. О, на самолете. Возьмем точку c на этой прямой на полюсах и обозначим расстояние os a.
Подставив формулы (1) и (3) в формулу (2), находим: С С, 1 с2 Величины, обратные коэффициентам упругости (жесткости), называются коэффициентами податливости. Людмила Фирмаль
Положение любой точки m является азимутом оси x, а плоскость zoa образована прямой ОА через m Точка Л1 этой плоскости на полюсах c2 имеет полярные координаты p и p. Координаты p, p, называются тороидальными координатами. Декартовы координаты выражаются в тороидальных координатах выражением x a p cos p cos, y a p cos p sin, z psin p. Найти коэффициент хромоты по формуле 6. ДСИ-wjdp, ДСТ hjlбыл Р, ДСА hadty. 1 Я заметила. Опций ИФП ds2 у ПД п, ДСА а п с cos Р Ф 2 Сравнение 1 и 2 7п 1, Н9 п ч А Р соз Ф. И проекция скорости на ось тороидальных координат ОП стр. Р п ПФ, П vp-р а pco8p Ф. Коэффициент скорости точки равен м п Р2Р а pco8p 2p2.
Точно так же у РФ 2rf а р соз ф ф ф греха .а pcosy Дик РcosФ а РcosФ 2Ф рсобф-рфэшф .Задача 14 .9 .Определите проекцию скорости на ось цилиндрической координаты см .рисунок .Решение .Зависимость декартовых координат от цилиндра выражается следующей формулой х СПКЯ п y psin р, з-з 1 Найти коэффициент хромоты Я я —, 1 −1 −1, ф— Х гр 1, Ф р1С01 ф р, 2 Проекции скорости на оси цилиндрических координат равны Выше СН, р р, V Ф ч р р р п, гг ч-р з .3 Задание 14 .10 .
Найти проекцию ускорения точки на ось цилиндрической системы координат см .рисунок в вопросе 14 .9 .Криволинейные координаты p, f и z определяют положение точки M в цилиндрической системе координат .Зависимость декартовых координат от цилиндра определяется уравнением Согласно 4 Шансы G и И г г Ищем проекцию ускорения на ось цилиндрической системы координат .Выяснить Р г г п п это не .И затем ..
Первые 2 уравнения представляют собой проекцию совпадения ускорения точки на полярную ось, которая используется в случае движения точки по плоскости. Задание 14. 11. Точка l1 движется по спирали в соответствии с уравнением х. -азоскт, 1 Дж Асин, 2 з БТ 3 Где a, k и b-константы. Определите уравнение траектории в цилиндрических координатах и ее скорость. Решение.
Цилиндрические координаты являются p yagh f yaz-g- Найти первые цилиндрические координаты Р 9и л Х2 j В а сопи 4 2-я цилиндрическая координата Р КТ. 5 3-я цилиндрическая координата задается непосредственно уравнением 3. Если исключить время из формул 3 и 5, то получим Это, наряду с уравнением 4, дает уравнение локуса точек, то есть спиральное уравнение цилиндрических координат. Спираль намотана на поверхность цилиндра радиуса a. Согласно задаче 14. 9 проекция скорости на цилиндрические координатные оси равна pp p. P 0 Потому что в этом случае p const.
- Следующий РФ РФ р-А, наконец. 1 р 7р-Х в. Задание 14. 12. Определяет проекцию скорости движущейся точки на ось эллипсоидной системы координат. Solution. In задача 14. 3, мы нашли хромые коэффициенты эллиптических координат rz и m 2, связанные с Декартовыми координатами уравнением. — — У 1. — У. И Ч1 2 4 А СФП В2 ПГ Где a, b-постоянные величины. Да. Хромые коэффициенты равны 1 ч — ч м 1 21в-Ш 2 2 В А С в М 2 в thxb н -з Проекция скорости на ось эллиптической системы координат так и будет — С.
Ум-2 А Г, М ме б ВН 0 1ДЖ, Никель Модуль скорости обратите внимание, что rz и t s должны находиться в пределах, указанных в выпуске 14. 3. Задача 14. 13. Уравнение движения точки задается уравнением в полярных координатах Р Р0 РВ, 1 Ф. 2 Определяет траекторию, скорость, ускорение, скорость вращения вентилятора и радиус кривизны трассы. Решение. Исключите время из выражений 1 и 2, чтобы найти Локус в явном виде Р стадо.
Изобразим груз в промежуточном положении, смещенным по от-пошению к началу отсчета направо на х, и представим, что он движется в сторону возрастания х, т. Людмила Фирмаль
Чтобы определить проекцию Скорость точки На оси полюса Рассмотрим значение коэффициента ламера см. Задачу 14. 9 К выпуску 14. 13. Яр 1, КШ п. 4 Затем, согласно 6 vp Нр р лров-лров —, 5 Р ф па бледно-ю. 6 Таким образом, коэффициент скорости равен 7 Направление скорости показано на рисунке. Согласно выпуску 14. 10, проекция ускорения на полярную ось равна и п п-пф2 А2р е- й2poe- 0, 8 АЛК 2пф р р — 2a2poe-Вт 9 Поэтому полное ускорение точки равно Вычислить тангенциальное ускорение, чтобы определить радиус кривизны траектории серии wx — У2 п в, 10 Нормальное ускорение равно Радиус кривизны орбиты 2р в 2 стая- Скорость работы отдела И 12 13 На плоскости.
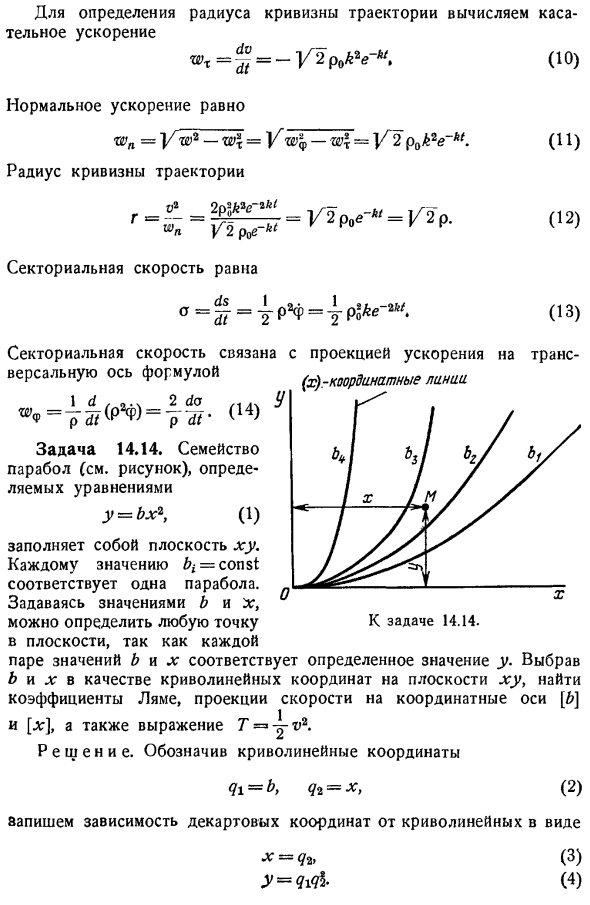
Пары значений b и x соответствуют конкретным значениям y. Выберите b и x в качестве криволинейных координат на плоскости xy и найдите коэффициент Ламера, проекцию скорости на координатные оси b и l и формулу t y. Решение. Маркировка криволинейных координат 2 Описывает зависимость декартовых координат от кривой в следующем виде Г Б. 3 4 Чтобы найти коэффициент хромого, сначала ст 5 6 Проекция скорости на криволинейную ось Координирует c1 h1 1×2b Р 2 я 4b2x л 7 8 9 ю Поскольку оси не ортогональны, используйте Формулы 3 и 5, чтобы найти Косинус углов между осями. Axes. In в этом случае произведение единичного вектора 3 определяет искомый Косинус неортогональной системы.
Не ноль по 11. Если ввести значение количества, которое требуется ввести в Формулу 11, то получится 12 Затем найти по теореме косинусов Н Х Т 2 d1tijcos 91, 1. 13 Если ввести значение для всех количеств в этой формуле, то 7- 4 m 2 1 2 bx 2bxjt. 14 Координатная линия x представляет собой параболу. Это потому, что каждый из них является b const. Координатные оси x касательны к параболе. Координатная линия b и ось b прямо параллельны оси y, x const. Задача 14. 16. Корабль движется с постоянной скоростью v и постоянным углом траектории a относительно географического меридиана. Определите проекцию ускорения на ось сферических координат, ускорение корабля и радиус кривизны траектории.
Решение. Выберите сферические координаты. In-широта, долгота положения корабля в p-сфере, r r const, где r- Радиус шара. Затем проекция скорости корабля на сферическую ось, ф 0, АЭ РД ocosa, в р cos6 osincc. Я Хромые коэффициенты сферических координат Ч л, ч р, Н9-rcos6. 3 Мы ищем прогнозы ускорения. А g-ось 3lf-0 Итак, wr — r6 — r cos0 f2 — 4 Б по оси 0 d4s. — r8co3 0. 51n8. П. Но из 2-го уравнения 1 системы 0 const, следовательно, 6 0. Далее, когда уравнение 1 задано мы 2- racos0-sin6 9 — y — tg6 5 c на оси Р j rcos 0 ф zi sin a r cos6 — nsina-r-sin 8-6 — p 8 — s — pc08a — о sin a cos a sin 0 Далее Обсудить 3 В9 — sinacosatg 8.
Ускорение корабля определяется по следующей формуле Ж М Ж 8 wj — v1 sin2 a tgj fl 7 Так как скорость корабля постоянна, а тангенциальное ускорение равно нулю, то он направлен вдоль главной законной линии локсодрома. Поскольку радиус кривизны lom равен v const, w Задача 14. 16. Пространственное движение точки задается уравнением движения цилиндрических координат. Р р 1 ом, f f01n 1 ЗП, з 20 л ф Где p0, 0, z0 и p-постоянные величины. Найти траекторию, скорость и ускорение точки, радиус кривизны траектории. Solution. In цилиндрические координаты, дифференциал дуги координатной линии равен СП ДП С4 ПРФ п ДСЗ ДЗ.
Сравните эти цитаты с хромой Формула с формулой 6, быстро найти коэффициенты 2 Используя формулу 6, можно найти проекцию скорости точки на цилиндрическую ось координат. ТТП-р по одному н ф ф — -. 3 Модуль скорости в ВФ х ИС Т yp pj i 0 4 — const 4 Прогнозирование ускорения в Формуле цилиндра. — Рф 2рф -. П р о. Определены оси pwi серебро 5 Модули ускорения равны 6 Поскольку скорость постоянна, тангенциальное ускорение равно нулю, а ускорение 6 — нормали acceleration. It определяет радиус кривизны траектории r из уравнения Откуда. .ПК г ае .p p pГ1 ф .
Смотрите также:
Предмет теоретическая механика

