Скорость точки
Известно, что при движении точки по прямой линии с постоянной скоростью, равномерно, скорость её определяется делением пройденного расстояния 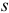 на время
на время 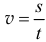 . При неравномерном движении эта формула не годится. И метод определения скорости зависит от способа задания движения.
. При неравномерном движении эта формула не годится. И метод определения скорости зависит от способа задания движения.
Скорость точки при векторном способе задания движения Пусть точка 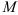 за малое время
за малое время 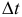 перешла из положения
перешла из положения 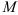 в
в 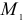 . При этом радиус-вектор её изменится на
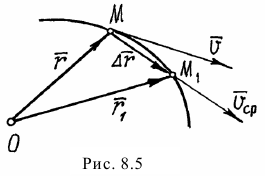
. При этом радиус-вектор её изменится на 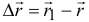 (рис. 8.5). Так как время
(рис. 8.5). Так как время 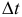 мало, можно предположить, что часть траектории
мало, можно предположить, что часть траектории 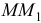 почти прямая, равна хорде
почти прямая, равна хорде 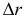 и движение близко к равномерному. Тогда приближённо скорость точки можно найти так:
и движение близко к равномерному. Тогда приближённо скорость точки можно найти так: 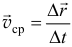 (так как
(так как 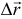 — вектор, то и
— вектор, то и 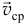 — вектор).
— вектор).
Конечно, чем меньше время 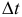 , тем ближе будет значение скорости к истинному. Поэтому
, тем ближе будет значение скорости к истинному. Поэтому
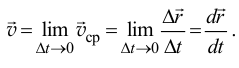
Итак, скорость точки есть производная от радиуса-вектора точки по времени
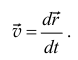
Направление вектора скорости v находим как предельное направление 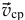 при
при 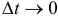 , то есть при приближении точки
, то есть при приближении точки 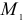 к точке
к точке 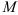 . Но такой процесс определяет касательную в точке
. Но такой процесс определяет касательную в точке 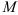 . Следовательно, вектор скорости
. Следовательно, вектор скорости 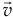 направлен по касательной к траектории и в сторону движения. И, наоборот, вектор скорости определяет направление движения точки в данный момент времени.
направлен по касательной к траектории и в сторону движения. И, наоборот, вектор скорости определяет направление движения точки в данный момент времени.
- Скорость точки при координатном способе задания движения
Как уже установлено, 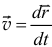 . Учитывая (8.1), получим:
. Учитывая (8.1), получим:
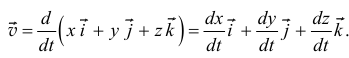
Вектор скорости как всякий вектор можно разложить на составляющие по осям
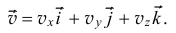
Сравнивая (8.2) и (8.3), устанавливаем, что проекции вектора скорости на оси есть первые производные от соответствующих координат по времени:
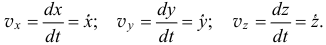
И модуль скорости
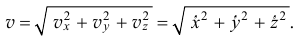
Направление вектора скорости можно определить графическим способом, откладывая в масштабе соответствующие составляющие вектора параллельно осям с учетом знака или с помощью направляющих косинусов
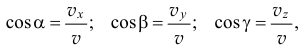
где 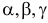 — углы между вектором
— углы между вектором 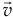 и направлениями осей
и направлениями осей 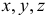 соответственно.
соответственно.
- Скорость точки при естественном способе задании движении
Величину скорости (см. п.1) можно определить как предел (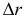 — длина хорды
— длина хорды 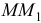 )
)
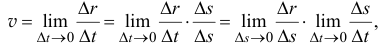
где 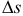 — длина дуги
— длина дуги 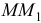 . Первый предел равен единице, второй предел производная
. Первый предел равен единице, второй предел производная 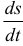 .
.
Следовательно, скорость точки есть первая производная по времени от закона движения
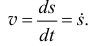
Направлен вектор скорости, как было установлено ранее, по касательной к траектории. Если величина скорости в данный момент будет больше нуля, то вектор скорости направляется в положительном направлении.
Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:
Помощь по теоретической механике
Кстати возможно вам будут полезны эти страницы:
| Трение качения |
| Способы задания движения точки |
| Ускорение точки |
| Поступательное движение тела |

