Скорость точки. Ее определение при задании движения точки векторным способом
Скоростью точки называется вектор, определяющий в каждый момент быстроту и направление движения точки.
Если точка в равные, произвольно взятые, промежутки времени проходит одинаковые расстояния, то ее движение называется равномерным, в противном случае движение точки называется неравномерным или переменным.
Как прямолинейное, так и криволинейное движение точки может быть или равномерным или неравномерным (переменным).
Размерность скорости
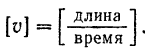
Каждому выбору единиц длины и времени соответствует своя единица скорости. Скорость может выражаться в м/сек, см/сек, км/час и т. д.
Рассмотрим случай криволинейного и неравномерного движения точки. Пусть некоторая точка, совершающая какое-либо движение по некоторой криволинейной траектории 
, в момент времени 
занимает на траектории положение 
, определяемое радиусом-вектором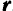 
, а в момент 
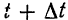— положение 
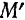, определяемое радиусом-вектором 
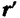(рис. 105). Проведем вектор из точки в точку .
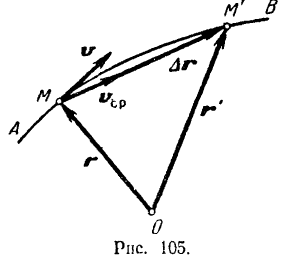
Вектор 
, соединяющий положение точки в начале данного промежутка времени с ее положением в конце этого промежутка, называется вектором перемещения
точки за этот промежуток времени. Из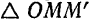 
видно, что 
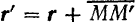Следовательно,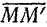 
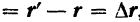, т. е. вектор перемещения 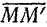точки равен геометрическому приращению 
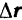ее радиуса-вектора .
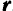Если мы представим себе, что точка 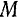получает за промежуток времени 
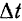то же перемещение 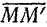=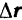, двигаясь не по дуге 
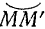(как это происходит в действительности), а по хорде 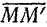, и притом двигаясь равномерно, то скорость такого фиктивного движения можно назвать вектором средней за рассматриваемый промежуток времени скорости точки
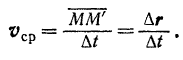
Так как от деления вектора на положительную скалярную величину получается вектор того же направления, то определяемый формулой (56) вектор средней за какой-либо промежуток времени скорости точки имеет направление (рис. 105) вектора 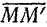ее перемещения и по модулю равен частному от деления модуля |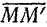| вектора перемещения точки на соответствующий промежуток времени.
Очевидно, что вектор средней скорости точки позволяет судить только о направлении ее конечного перемещения за рассматриваемый промежуток времени и о некоторой средней быстроте этого-перемещения, но не дает представления о действительном направлении и действительной быстроте движения точки в любой момент времени.
Очевидно, что вектор v скорости точки в данный момент времени равен пределу вектора ее средней скорости за промежуток времени, начинающийся в этот момент, когда величина промежутка стремится к нулю.
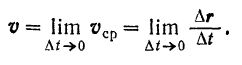
Так как 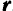есть векторная функция скалярного аргумента 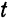, то
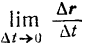
есть векторная производная этой функции. Обозначая эту производную аналогично производной от скалярной функции символом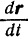 
, будем иметь
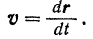
Скорость v точки равна первой производной от радиуса-вектора этой точки по времени.
Так как вектор средней скорости точки 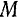направлен по вектору перемещения 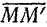, а в пределе, при неограниченном стремлении 
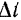к нулю, соответствующая секущая совпадает с касательной в точке 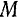, то вектор v скорости точки в каждый момент направлен по касательной к траектории в соответствующей точке в сторону движения точки (рис. 105).
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
