Оглавление:



Скорость точки
- Одной из главных особенностей движения точки является скорость относительно выбранной системы отсчета. Это показано в виде декартовой декартовой системы координат (рис. 1). Положение точки M перемещения относительно рассматриваемой системы отсчета определяется вектором мгновенного / радиуса r. Радиус-вектор r связывает неподвижную точку O с этой точкой.
Движущаяся точка принимает вектор, а r-точка изменяется следующим образом Другим моментом t1 = t + At является положение Mt и его радиус-время D / радиус перемещения Dg = r (-r Средняя скорость gd точек в течение Dg называется соотношением DgfAt. Vcp = Dg / ‘Lg. Скорость параллельна веку 13 распространенных случаев Средний тор Со времени усреднения Dg. У нее нет конкретной точки приложения на пути. Представляя скорость точка Если период, в течение которого определяется средняя скорость, имеет тенденцию быть нулевым, то есть v в момент r, определенный как предел средней скорости v = lim aCp = lim Ar / Az = df / dz. -о-AG-о.
Последнее указывает на то, что вращение Земли должно быть отражено во вращении колеблющейся поверхности математического маятника вокруг вертикали этого места и в направлении движения в течение дня знаменитого прохода пантеона. Людмила Фирмаль
Является ли скорость точки направленной на движение в предельном направлении вектора Dt? Тенденция равна нулю, то есть ограничивающему направлению секущей MMt, которое совпадает с касательной к орбите в точке M. Следовательно, скорость точки равна первой производной. От его радиус-вектора. Это направлено вдоль траектории касательной в направлении точки. Начальная точка вектора радиуса движущейся точки может быть выбрана в любой фиксированной точке. На рисунке 1 показан случай, когда p, начиная с точки O, также является радиус-вектором. Радиус-векторы r и p имеют одинаковое изменение Dg и Dp в течение времени D /, и, следовательно, v = dr / dT = dp / ‘dt (1).
- Измерение скорости SI берется из (1). [у] = длина / длина = м / с. Во многих случаях скорость выражается в км / ч. км / ч = 3,6 в м / с. Концепция годографа используется для характеристики переменных векторов. Векторный годограф — это геометрическое расположение обоих концов, когда переменный вектор откладывается от одной и той же общей точки в разное время. Точечная траектория является явно годографом радиус-вектора r или p (рис. 1). В этом случае последовательные положения вектора F в различные моменты времени откладываются от точки O, а вектор p откладывается от точки O ‘.
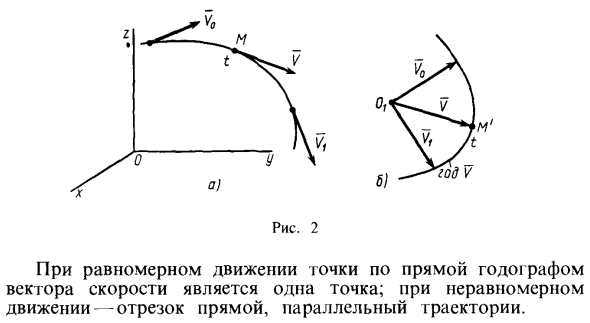
Первая производная по времени от радиус-вектора — это скорость точки, направленной по касательной к траектории. Таким образом, параллельно тангенсу годографа получается первая производная любого скалярного аргумента переменного вектора. Годограф вектора скорости — это линия, расположенная в другой момент времени, когда ребра этого вектора начинают соединяться в общей точке. Чтобы создать годограф вектора скорости, выберите точку, например О (рисунок 2.6), и перенесите начальную точку вектора скорости в разное время в эту точку, не меняя значения и направления. Каждая точка траектории M (рис. 2, а) соответствует собственной точке рисования M ‘на годографе вектора скорости (рис. 2.6).
Наиболее распространенным методом изучения всех явлений природы и общества является признание опыта как источника всех знаний и акцент на абстрактное мышление с моделями явлений. Людмила Фирмаль
Шкала скорости при создании годографа вектора скорости может отличаться от шкалы скорости, отображаемой в точках траектории. Когда точка движется по траектории, соответствующая точка изображения движется вдоль годографа вектора скорости. Если точки движутся по прямой линии, годограф вектора скорости равен 1 точке. Для неравномерного движения — отрезок прямой, параллельный траектории.
Смотрите также:
Задачи по теоретической механике
| Объем пирамиды и конуса | Ускорение точки |
| Объем полушара | Векторный способ изучения движения |
Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.

