Оглавление:




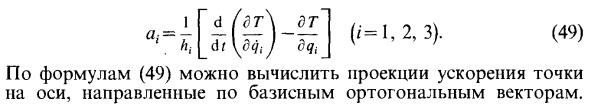

Скорость и ускорение точки в криволинейных координатах
- Положение точки в пространстве декартовой системы координат определяется тремя координатами: x, y и g. Другие три параметра qx, q2, q3 можно выбрать и назвать криволинейными координатами точки или общими координатами.
Применительно к первому и второму этапу теоремы о точке столкновения, для изменения импульса, проецируемого в направлении внешней нормали к поверхности, скорость точки до столкновения противоположна. Людмила Фирмаль
Декартовы координаты зависят от кривой: x = x (qlt q2, q3) ‘, Y = Y (Ch1, 9g-9z); 2 = 2 (9, 9s> 9s) — Движение точки в криволинейных координатах задается уравнением . «7, Du Действительность тождества (44) установлена. Различают v от / ol, чтобы доказать идентичность (45) \ -_ DV _ DGG. DGG. d2g. dqt dqtdq ^ 1 dqfiq * ‘ D не может полагаться на обобщенное и не может дифференцироваться как сложное во времени (46) На рассмотрении скорость.
- Функция времени у нас есть др \ е4л + +, 47> (46) и (47) находятся на правой стороне. Это связано с тем, что частные производные отличаются только порядком независимых частных производных. Таким образом, тождество (45) доказано. Используйте идентичность, чтобы преобразовать выражение в скобках из (42). получить 2, и введение функции T = — Учитывая (48) <4 ” Уравнение (49) позволяет рассчитать проекцию ускорения точки на ось вдоль базиса ортогонального вектора.
Если точка находится не в этом положении, но ей задана скорость движения дула в направлении этого положения, достаточно большая, чтобы пройти через это положение, то это будет второе притяжение. Людмила Фирмаль
Если твердое тело под действием трех сил пересекается в одной точке, то оно находится в равновесии, где линии действия таких трех сил пересекаются в одной точке. Таким образом, три силы пересекаются в одной точке. Теорема о трех силах позволяет в некоторых случаях определить линию действия неизвестной силы, приложенной к твердому телу.
Смотрите также:
Задачи по теоретической механике
Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.

