Сходимость рядов Фурье для функций, удовлетворяющих условию Гёльдера

Оглавление:

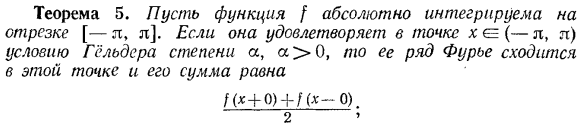
Сходимость рядов Фурье для функций, удовлетворяющих условию Гёльдера

Сходимость рядов Фурье для функций, удовлетворяющих условию Гёльдера. В этом подразделе показано условие, которое достаточно слабее условия односторонней Дифференцируемости (см. Результат теоремы 55.4 4, 2).Длина / значение, равное периоду функции (55.26). Определение 9.Функция, определенная в интервале (xy, b), называется функцией, удовлетворяющей правостороннему условию Гельдера степени a в x0, если существует конечная правосторонняя f (x0-1-0) и константы M0 и 60.Любое неравенство, удовлетворяющее условию 0 s / g 6 !(Хе + ч) −1(Хо + 0)\ Мга. (55.33） Функция/, определяемая интервалом (a, xn), называется функцией, удовлетворяющей левому ограничению/(x0-0) и постоянной M0 и 6 0, если существует функция, удовлетворяющая условию Гельдера слева от степени a в точке x0.

Функция, определенная для сегмента, называется функцией, удовлетворяющей определенной степени условия сегмента, если она удовлетворяет степени условия, заданного в каждой точке, и если она расположена как слева, так и справа в каждой внутренней точке сегмента. Людмила Фирмаль

Удовлетворяют условию 0 / g 6, неравенство | /(x0-й)-/(x0-0)|me. (55.34)） Функция, удовлетворяющая условию держателя как справа, так и слева в определенной точке x (), называется функцией,§ 55.Тригонометрический ряд Фурье 366. В точке задачи выполняются условия держателя определенной степени. Левый край сегмента-правая сторона, а правый-левая сторона. Следует отметить, что так называемые классические условия Гельдера этой степени таковы: функция/называется, Если 8 0 и 7И0 существуют для всех k, то в точке x удовлетворяет классическому условию Гельдера порядка a 0.

В 6 лет неравенство ((х^ к)-[(Х)| М \ к|». Очевидно, что в этом случае по условию и 0 функция/всегда непрерывна в точке x. PT | f | / = from 0, After 0 о-о. Это будет Tm f(x + f)= f (l). * ■О Аналогичным образом определяются классические условия Гельдера в одном направлении. Таким образом, различие между рассматриваемым условием Гельдера и классическим заключается в том, что, в частности, согласно нашему определению, функция, удовлетворяющая условию Гельдера, в какой-то момент может быть разрывной. 1 следующее условие Гельдера обычно называют условием Липшица. Упражнение. 7.Если функция в какой-то момент удовлетворяет условию держателя порядка a, то 0 p a доказывает, что она также удовлетворяет условию держателя порядка{5 в этой точке. 8.

Если функция имеет ограниченную производную на интервале, то это доказывает, что она удовлетворяет условию Липшица с той же константой M. 9.Если функция удовлетворяет классическому условию Гельдера порядка a 1 на некотором интервале, то она оказывается постоянной на этом интервале. 10.Функция [(х)= ХД, xm0, 0 = а = С1 доказывает, что Х = 0 удовлетворяет владельца состояние заказа и не удовлетворяет владельца состояние степень в ней. Теорема 5.Предположим, что абсолютная интегрируемость возможна с функцией [интервал [π, π].Точка x e. если (I, z) удовлетворяет условию Гельдера a, 0 степени a, то его ряд Фурье сходится в этой точке, и его сумма равна /(Б°-0). 2 ’ Р. Липшиц (1832-1903) немецкий математик. 55.5.

Сходимость рядов Фурье 367. В частности, если функция непрерывна в точке x CE (i, i), то ее ряд Фурье сходится в этой точке к значению функции. Золото 5N(р, ф)= ф (). П+ 00 Если функция / удовлетворяет правому условию Гердера в точке x = pi слева в точке x = n, то ее ряд Фурье сходится в этих точках, и его сумма равна /（Два Доказательство. выберите δ, 0δ.Во-первых, пусть интервал[0, δ] не имеет другой особенности функции П(0. Вероятно, за исключением точки x = 0, и тогда、 Все функции H,| H / b / удовлетворяют условию держателя (55.33) и (55.34) в точке x. тогда по формуле (55.22) функции (/)、 Тогда/(x + 0-I(x+ 0）+ /（-0-/（*-0） {1 1 2 метра Район б Г * С1（ Потому что интеграл\ a 0 сходится.

В заключение отметим, что если функция f точки x имеет правую производную, то f удовлетворяет условию Гёльдера порядка 1 в этой точке справа. Людмила Фирмаль

В этом случае Интеграл (55.25) также сходится. Таким образом, теорема 5 вытекает из теоремы 4.Ноль Фут/（* + ）-/（ + 0）= р(х） Н + О П Все Н.) | r / b, неравенство будет справедливым ■Г +(х） Один СХ + Х) РХ + 0） К Оттуда, положив М-| / +（*）| + 1、получить М Пх + Б) П * + 0) м; Для этого | /(х + / р)-/(х + 0)| Л4 | / 1|, | / г / Б. Конечно, подобное описание применимо и к производным слева. § 55.Тригонометрический ряд Фурье 368. Выпуск 35.Функция / определена в интервале[a, b\, для каждой пары точек x и x + + + того этого отрезка, x ∈ [a, b], x+ / g e[a.

Интеграл Дирихле. Принцип локализации.	Суммирование рядов Фурье методом средних арифметических.
Сходимость рядов Фурье в точке.	Приближение непрерывных функций многочленами.