Оглавление:




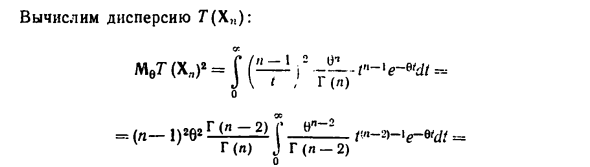







Скалярный параметр
- Обращаясь к проблеме параметрической объективной оценки : Koi 1 |) \ nktsni cp (8) модель (Г, JS,) [Pq, 8ev}). Т (х) Достаточно статистики. Как установлено в §17, Эффективность оценки, чтобы принять величину дисперсии Без потерь ограничимся оценками вида S (x) = g (T (x)) Эффективность. Если оценка требуется в форме / (V (x)), Если статистика V (x) недостаточна, происходит потеря Эффективность, когда / j (V (X)) не соответствует g (T (X)) Pg вероятностная единица, 8ev. Интересно, проиграв Эффективность объективной оценки Прямо через количество информации Фишера. напоминание
Помните, что информация Фишера не теряется при путешествии из свести b’borkp x к достаточной статистике T (x) и наоборот Проход по статистике V (x) будет уменьшаться, но не достаточно Достаточно 7 М.В. Козлов, А.В. Прохоров 185 Как основа логарифма в определении 1 \ @. в Возьми номер е. Пример вклада — ценность {f (x; u = — \ n [(x; 0) или -1nPe (x), A> от Для непрерывных или дискретных моделей соответственно.
В случае Для повторных независимых наблюдений ? / (X „; 8)« ?? / (* ,; 0), Где U (xi \ 9) называется вкладом наблюдаемого Xt и определяется В той же формуле, что и в А). Людмила Фирмаль
Предположим, мы встретились Условие D9) §18: Mf / (Xi; 9) = 0, В) Из б) / x „F) = DeU (X„; 6) -? D (IU (A ‘,; 0) -1 / , @). Следующее доказывает, что есть закономерность при определенных условиях Дисперсия несмещенной оценки 5 (х) =? (T (x)), где T (x) T (x) — Фреше — Рао — случайная статистика, удовлетворяющая неравенству Крамер: C) Если статистика T (qc) достаточна, fm (x> @) -> x ( Неравенство в) DbS (X)> 4> ‘(u) s /’ x @). D) Если статистика T (X) недостаточна (см. § 18§4) / та, @) ! Xn): Xi = 0 или 1, =? == I ….. l}, Pb (xn) = 6Γ (x «) A-6) n-T (x»), Γ (xn) = y xit 0 <6 <1. Оптимальная несмещенная оценка для параметра b имеет дисперсию DG- (Xn) M) = 9 (1-9) / n.
Используйте независимость, чтобы рассчитать информацию о Фишере, Равнораспределение эл.в. Ци …, Х „: с того времени (Al In6 + A dg ±) ln (10)) = .ve = (N-1-c) / Ch0A-O)), тогда Следовательно, в этом случае неравенство E) равно. (II) Для образцов из экспоненциальных измерений распределения Pb, 9> 0 определяется плотностью = 6 «EXP (~ 6 Дж я — я Наилучшая несмещенная оценка 0 равна (см. Пример (I) §17) Вычислить дисперсию G (X „). о G (n-2) «» n ~ 2 б 187 О * G (n) J G (n-2)
- Г (л) л -2 То есть «-e» = — ^. F) Рассчитать информацию Фишера. Форма неравенства E) n G) Следовательно, минимально достижимая дисперсия F) равна Несмещенная оценка для параметра 6 больше границы G) Фреше— Лао Крамер. Если n большое, несоответствие между F) и G) Я могу игнорировать это. Если параметрическая функция 0}. A2) Очевидно, что если соотношение A0) верно, то (8) выполнено.
A4) При повторении независимой выборки получается уравнение (9). Принять форму А требование А3) можно обобщить следующим образом: = О. А5) Еще одно требование для сертификации Неравенство D), способность переносить дифференциальные операции Дифференцирование по признаку интеграла формулы: = — ^ — | … JS (x) / x (x; … дхн. A6) Учитывая условие A4), соотношение A6) Форма (ср. А1))
И только когда j ^ — / x (x; e) dx1 … dxn = O. A3) Когда выполняется соотношение A3) -? — / x (x; 6) = 0 для xe # e # c. Людмила Фирмаль
@) и дис- рассеивание DeS (X), Oe? / (X; c) = / x (c), Выполняется неравенство D), оно меняется одинаково Только если S () линейная функция Пример ввода: ; 0) А8) «Вероятность», которая является подмножеством P. Доказательство. Условия теоремы предполагают связь (8) и А7). Используя (8), перепишите A7) в следующий формат <p ‘(e) = M (S (X) — <p @))? / (X; 0). Неравенство Коши-Шварца-Бняковского V ‘(eJ <DeS (X) Det / (X; c), Равенство достигается только при выполнении условия A8). Если вам нужно доказать. | Примечания 1. Для дискретных моделей все Предыдущие соображения для замены плотности с распределением Вероятность и интегральное распределение для суммы.
Замечания 2. Когда T (X) = (Γ, (X), …, Γ (X)) является статистикой -Статистика и fr (V, 0) удовлетворяют условию теоремы 1. Имеет место несмещенная оценка-функция T (X) -неравенство C). Результатом неравенства D) является От А8 для всех * 9ев) ^ @) — 1, А9) О) / x (x, G) -h (x) exp (A (Q) S (x) + B (G)), B0) В то же время B / (c) / A ‘(c) = -φ (c). B1) И наоборот, если формат / x (x; 0) равен B0), A9) равен true, Следовательно, A8), а именно неравенство Фреше-Лао-Крамера D) Быть равным Таким образом, обратное неравенство D) Уравнение справедливо только для показательных функций Модель B0) и aS (x) + p (a, P- Любая константа) или параметрическая Особенности формы (Yi b — произвольная постоянная).
Смотрите также:
| Информация по Кульбаку | Векторный параметр |
| Информация по Фишеру | Границы дисперсии при нарушении условий регулярности |
Если вам потребуется заказать статистику вы всегда можете написать мне в whatsapp.

