Оглавление:
Определение скалярного произведения
Скалярным произведением двух ненулевых векторов 
и 
называется число, равное произведению длин этих векторов на косинус угла между ними.
Обозначается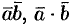 
(или (, )). Итак, по определению,
где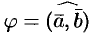 
.
Формуле (6.1) можно придать иной вид. Так как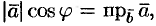 
(см. рис. 14), а 
, то получаем:
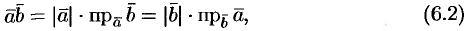
т. е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.
Свойства скалярного произведения
1. Скалярное произведение обладает переместительным свойством: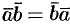 
.
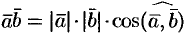, а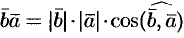 
. И так как 
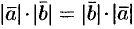, как произведение чисел и 
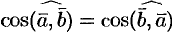, то .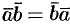
2. Скалярное произведение обладает сочетательным свойством относительно скалярного множителя: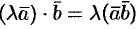 
.
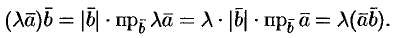
3. Скалярное произведение обладает распределительным свойством: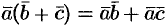 
.
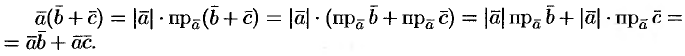
4. Скалярный квадрат вектора равен квадрату его длины: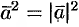 
.
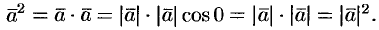
В частности: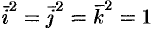 
.
Если вектор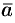 
возвести скалярно в квадрат и затем извлечь корень, то получим не первоначальный вектор, а его модуль 
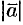, т. е. 
.
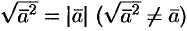Пример №6.1.
Найти длину вектора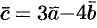 
, если 
, 
.
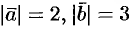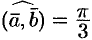Решение:
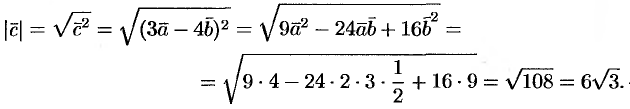
5. Если векторы и (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если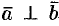 
, то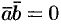 
. Справедливо и обратное утверждение: если 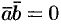и 
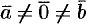, то .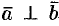
Так как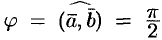 
, то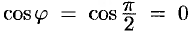 
. Следовательно, 
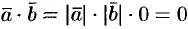. Если же 
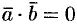и 
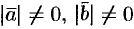, то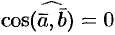 
. Отсюда 
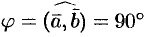, т. е. 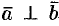. В частности:
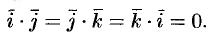
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Проекция вектора на ось |
| Разложение вектора по ортам координатных осей |
| Выражение скалярного произведения через координаты |
| Некоторые приложения скалярного произведения |
