Оглавление:
Возможны две операции умножения двух векторов. Одна дает в результате скаляр (число) и поэтому называется скалярным произведением. Другая дает в результате вектор — векторное произведение.
Определение. Скалярным произведением двух векторов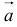 
и 
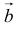называется произведение их модулей на косинус угла между ними.
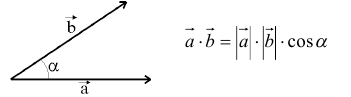
Из определения следует: 1) если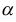 
— острый угол, то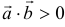 
2) если 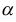— тупой угол, то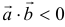 
3) если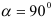 
, то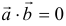 
Справедливы и обратные утверждения.
Физический смысл скалярного произведения
Работа постоянной силы при прямолинейном перемещении ее точки приложения равна скалярному произведению силы на вектор перемещения: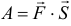 
.
Законы и свойства скалярного произведения
1. 
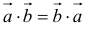(переместительный);
2. 
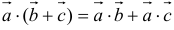(распределительный);
3. 
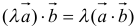(сочетательный);
4. 
;
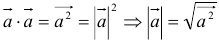5. 
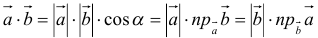— скалярное произведение равно произведению модуля одного вектора на проекцию другого вектора на первый.
Скалярное произведение в координатах
Пусть два вектора 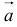и 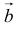разложены по ортам: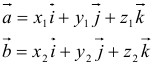 
Тогда: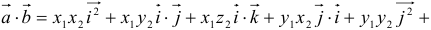 
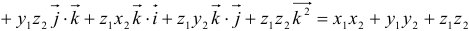, т. к.
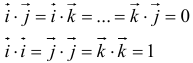
Итак, скалярное произведение двух векторов равно сумме произведений их соответствующий проекций:
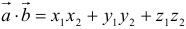
Применение формул скалярного произведения
Вычисление угла между векторами
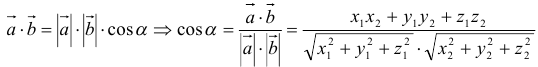
Вычисление проекции одного вектора на другой:
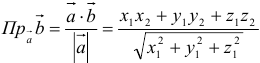. Аналогично: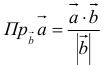 
Вычисление работы силы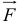 
на перемещении 
:
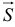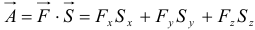, где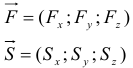 
Условие перпендикулярности двух векторов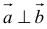 
:
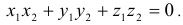
Решение задач
Задача №1.
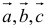— единичные векторы, составляющие соответственно с осью 
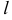углы 45°, 60°, 120°. Вычислить проекцию вектора 
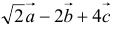, на ось .
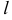Решение:
В соответствии со свойствами проекций имеем:
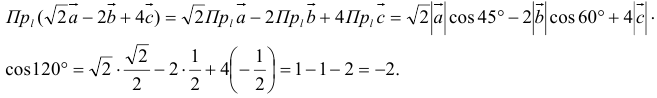
Ответ: -2.
Задача №2.
Определить, при каких значениях 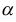и 
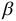векторы 
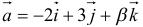и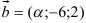 
коллинеарны? В ответе записать 
.
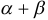Решение:
Если существует такое числ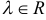о 
, что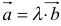 
, то векторы коллинеарны: 
.
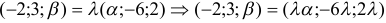У равных векторов равны соответствующие координаты, следовательно
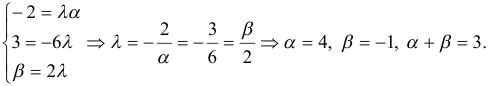
Второй способ решения. Если векторы коллинеарны, то их координаты пропорциональны т. е.
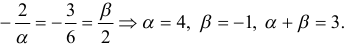
Ответ: 3.
Задача №3.
Вычислить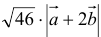 
, если 
.
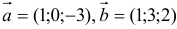Решение:
1) Находим координаты векторов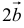 
и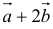 
:
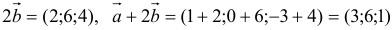
2) Находим длину вектора :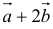
.
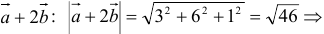
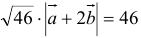Ответ: 46.
Задача№4.
Вычислить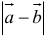 
, если 
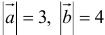, угол 
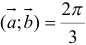. В ответе запишите квадрат длины вектора 
.
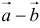Решение:
1) 
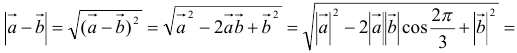
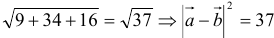
Ответ: 37.
Задача №5.
Вычислите работу силы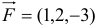 
, если ее точка приложения, двигаясь прямолинейно, перемещается из точки 
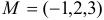в точку 
.
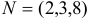Решение:
Пусть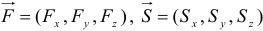 
.
Тогда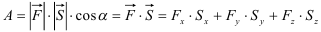 
Так как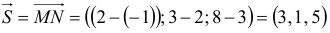 
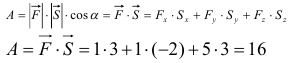
Ответ: 16.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Проекция вектора на ось |
| Действия над векторами, заданными координатами |
| Полярная система координат |
| Цилиндрическая система координат |
