Оглавление:
Рассмотрим систему неравенств
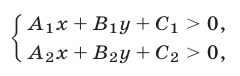
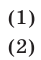
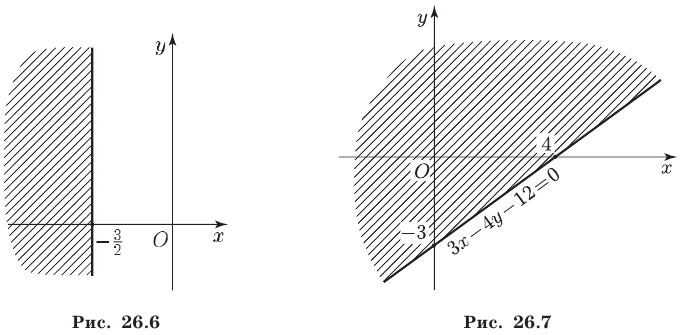
предполагая, что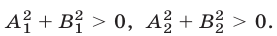 
Тогда неравенству (1) удовлетворяют точки множества 
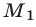, лежащие по одну сторону от прямой 
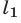, заданной уравнением
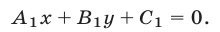
Аналогично, множество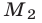 
— одна из полуплоскостей, на которые разбивается координатная плоскость прямой 
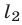, заданной уравнением
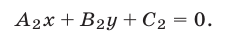
Множество решений системы (1), (2) представляет собой пересечение множеств 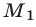и .
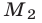Примеры с решениями
Пример №315.
Решить систему неравенств
Решение:
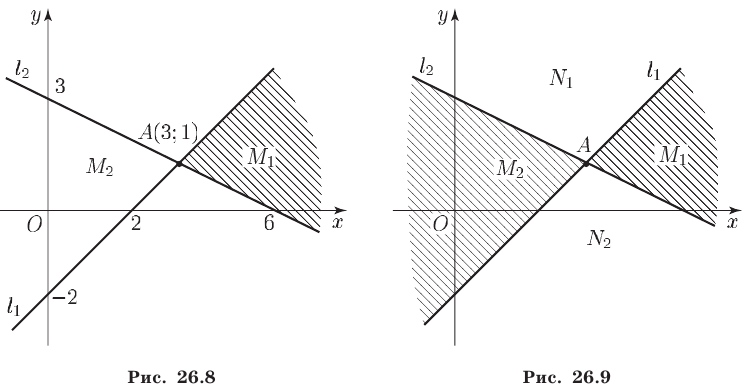
Построим прямые 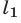и 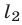(рис. 26.8), заданные соответственно уравнениями
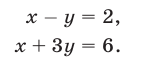
Решив систему (5), (6), получим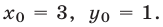 
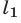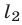Следовательно, прямые и пересекаются в точке 
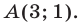Так как координаты точки 
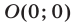не удовлетворяют ни одному из неравенств (3), (4), то системе неравенств (3), (4) удовлетворяют координаты тех и только тех точек координатной плоскости, которые лежат ниже прямой 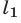и выше прямой 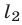, т. е. точки угла 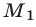с вершиной 
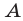, заштрихованного на рис. 26.8. Аналогично решаются системы неравенств, получаемые из системы (1), (2) заменой одного или двух знаков неравенств на противоположные.
Если пересекающиеся в точке 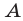прямые 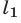и 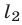(рис. 26.9) задаются соответственно уравнениями
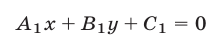
и
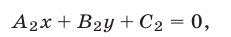
то неравенство
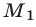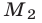определяет либо объединение одной пары и вертикальных углов с вершиной 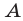(рис. 26.9), либо объединение другой пары 
и
вертикальных углов с той же вершиной.
В самом деле, во всех точках каждого из множеств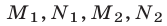 
левая часть неравенства (7) принимает либо положительные, либо отрицательные значения, а при переходе от одного из этих множеств к соседним (через одну из прямых 
) знак левой части этого неравенства меняется на противоположный.
Если, например, на множестве 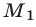левая часть неравенства (7) положительна, то на множествах и она будет отрицательной, а на 
— положительной.
Чтобы определить, на каком из двух множеств 
или 
справедливо неравенство (7), достаточно определить знак левой части этого неравенства в какой-либо точке одного из множеств 
Пример №316.
Решить неравенство
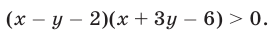
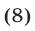
Решение:
Неравенство (8) равносильно совокупности систем неравенств
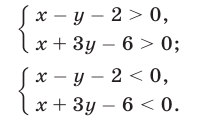
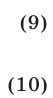
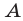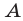Множеством решений системы (9), равносильной системе (3), (4), является угол с вершиной (заштрихованный на рис. 26.8), а множеством решений системы (10) — угол с той же вершиной , содержащий точку 
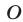. Объединение этих углов представляет собой множество всех решений неравенства (8).
Пример №317.
Решить систему неравенств
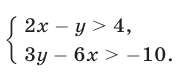
Решение:
Второе неравенство этой системы равносильно неравенству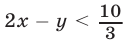
и поэтому исходная система равносильна следующей:
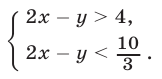
Если бы пара чисел 
была решением этой системы, то число 
удовлетворяло бы двум условиям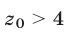 
и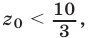 
что невозможно. Следовательно, исходная система неравенств не имеет решений.
Пример №318.
Найти множество точек координатной плоскости, удовлетворяющих системе неравенств
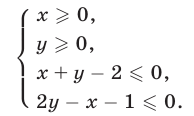
Решение:
Первым двум неравенствам системы (11) удовлетворяют все точки, у которых обе координаты неотрицательны, т. е. точки, лежащие в I квадранте (включая точки положительных полуосе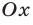й 
и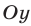 
).
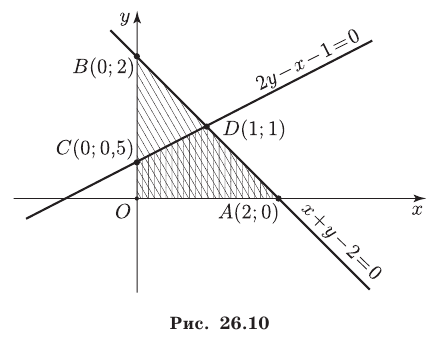
Чтобы решить неравенство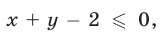 
рассмотрим прямую 
(рис. 26.10).
Эта прямая проходит через точки 
и 
. При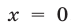 
, 
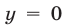неравенство 
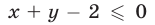является верным. Следовательно, неравенству 
удовлетворяют все точки, лежащие ниже прямой 
и на самой прямой. В результате получаем, что первым трем неравенствам системы (11) удовлетворяют точки, расположенные внутри и на границе треугольника с вершинами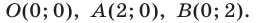 
Решим, наконец, последнее неравенство системы (11), т. е. неравенство 
Рассмотрим прямую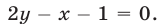 
Полагая 
находим 
Таким образом, прямая проходит через точку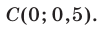 
Найдем точку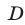 
пересечения прямой 
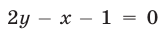с прямой 
Для этого решим систему уравнений
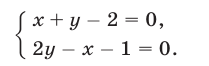
Складывая уравнения системы (12), получаем 
, откуда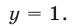 
Подставляя 
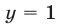в первое уравнение системы (12), находим 
. Значит, точка 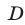имеет координаты 
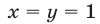(рис. 26.10).
Так как неравенству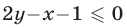 
удовлетворяют точки, лежащие ниже прямой 
(точка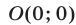 
удовлетворяет этому неравенству), то системе (11) удовлетворяют все точки, лежащие внутри и на границе четырехугольника 
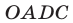(рис. 26.10).
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
