Оглавление:
Системы линейных однородных уравнений
Пусть дана система линейных однородных уравнений
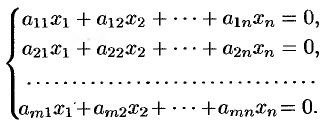
Очевидно, что однородная система всегда совместна 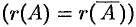 , она имеет нулевое (тривиальное) решение
, она имеет нулевое (тривиальное) решение  .
.
При каких условиях однородная система имеет и ненулевые решения?
Теорема 4.4. Для того, чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг 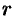 ее основной матрицы был меньше числа
ее основной матрицы был меньше числа 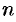 неизвестных, т. е.
неизвестных, т. е. 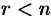 .
.
Необходимость.
Так как ранг не может превосходить размера матрицы, то, очевидно, 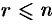 . Пусть
. Пусть 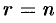 . Тогда один из миноров размера
. Тогда один из миноров размера  отличен от нуля. Поэтому соответствующая система линейных уравнений имеет единственное решение:
отличен от нуля. Поэтому соответствующая система линейных уравнений имеет единственное решение: 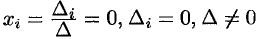 . Значит, других, кроме тривиальных, решений нет. Итак, если есть нетривиальное решение, то
. Значит, других, кроме тривиальных, решений нет. Итак, если есть нетривиальное решение, то 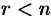 .
.
Достаточность.
Пусть 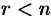 . Тогда однородная система, будучи совместной, является неопределенной. Значит, она имеет бесчисленное множество решений, т. е. имеет и ненулевые решения.
. Тогда однородная система, будучи совместной, является неопределенной. Значит, она имеет бесчисленное множество решений, т. е. имеет и ненулевые решения.
Пусть дана однородная система 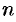 линейных уравнений с
линейных уравнений с 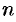 неизвестными
неизвестными
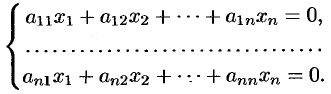
Теорема 4.5. Для того, чтобы однородная система 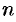 линейных уравнений с
линейных уравнений с 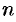 неизвестными имела ненулевые решения, необходимо и достаточно, чтобы ее определитель
неизвестными имела ненулевые решения, необходимо и достаточно, чтобы ее определитель  был равен нулю, т. е.
был равен нулю, т. е. 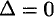 .
.
Если система имеет ненулевые решения, то 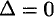 . Ибо при
. Ибо при 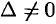 система имеет только единственное, нулевое решение. Если же
система имеет только единственное, нулевое решение. Если же 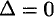 , то ранг
, то ранг 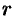 основной матрицы системы меньше числа неизвестных, т. е.
основной матрицы системы меньше числа неизвестных, т. е. 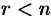 . И, значит, система имеет бесконечное множество (ненулевых) решений.
. И, значит, система имеет бесконечное множество (ненулевых) решений.
Пример №4.6.
Решить систему
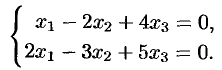
Решение:
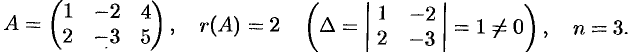
Так как 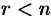 , то система имеет бесчисленное множество решений. Найдем их
, то система имеет бесчисленное множество решений. Найдем их
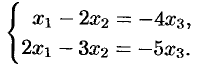
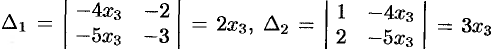 . Стало быть,
. Стало быть, 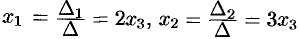 — общее решение.
— общее решение.
Положив 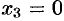 , получаем одно частное решение:
, получаем одно частное решение: 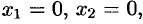
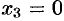 . Положив
. Положив 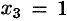 , получаем второе частное решение:
, получаем второе частное решение: 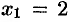 ,
, 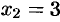 ,
, 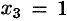 и т. д.
и т. д.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Действия над матрицами |
| Элементарные преобразования матриц |
| Линейные операции над векторами |
| Проекция вектора на ось |

