Оглавление:
Системы линейных ДУ с постоянными коэффициентами
Рассмотрим еще один метод интегрирования нормальной системы уравнений (52.1) в случае, когда она представляет собой систему линейных однородных ДУ с постоянными коэффициентами, т. е. систему вида
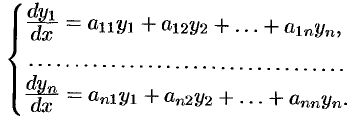
Для простоты ограничимся рассмотрением системы трех уравнений с тремя неизвестными функциями 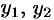 и
и 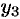 :
:
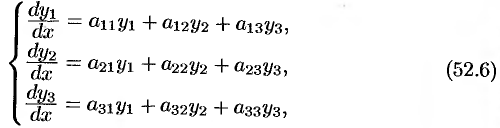
где все коэффициенты 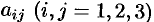 — постоянные.
— постоянные.
Будем искать частное решение системы (52.6) в виде
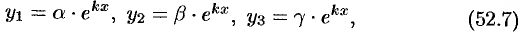
где 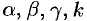 — постоянные, которые надо подобрать (найти) так, чтобы функции (52.7) удовлетворяли системе (52.6).
— постоянные, которые надо подобрать (найти) так, чтобы функции (52.7) удовлетворяли системе (52.6).
Подставив эти функции в систему (52.6) и сократив на множитель 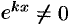 , получим:
, получим:
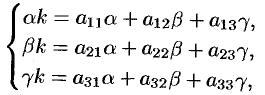
или
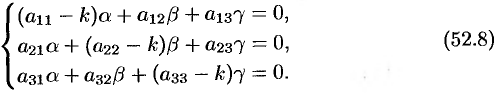
Систему (52.8) можно рассматривать как однородную систему трех алгебраических уравнений с тремя неизвестными 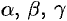 . Чтобы эта система имела ненулевое решение, необходимо и достаточно, чтобы определитель системы был равен нулю:
. Чтобы эта система имела ненулевое решение, необходимо и достаточно, чтобы определитель системы был равен нулю:
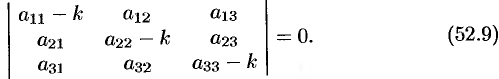
Уравнение (52.9) называется характеристическим уравнением системы (52.6). Раскрыв определитель, получим уравнение третьей степени относительно 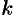 . Рассмотрим возможные случаи.
. Рассмотрим возможные случаи.
Случай 1. Корни характеристического уравнения действительны и различны: 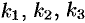 . Для каждого корня
. Для каждого корня 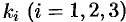 напишем систему (52.8) и определим коэффициенты
напишем систему (52.8) и определим коэффициенты 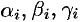 (один из коэффициентов можно считать равным единице). Таким образом, получаем:
(один из коэффициентов можно считать равным единице). Таким образом, получаем:
- для корня
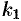 частное решение системы (52.6):
частное решение системы (52.6): 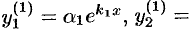
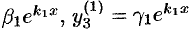 ;
; - для корня
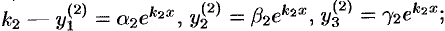
- для корня
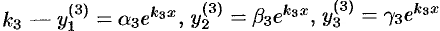 .
.
Можно показать, что эти функции образуют фундаментальную систему, общее решение системы (52.6) записывается в виде
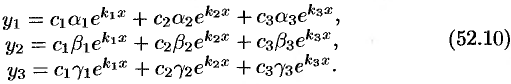
Пример №52.3.
Решить систему уравнений:
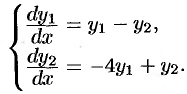
Решение:
Характеристическое уравнение (52.9) данной системы имеет вид
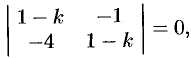
или 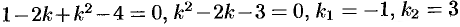 . Частные решения данной системы ищем в виде
. Частные решения данной системы ищем в виде 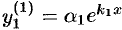 ,
, 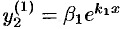 и
и 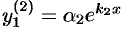 ,
, 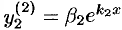 . Найдем
. Найдем 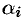 и
и 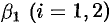 .
.
При 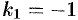 система (52.8) имеет вид
система (52.8) имеет вид
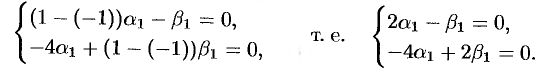
Эта система имеет бесчисленное множество решений. Положим 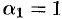 , тогда
, тогда 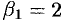 . Получаем частные решения
. Получаем частные решения
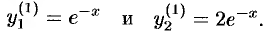
При 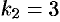 система (52.8) имеет вид
система (52.8) имеет вид
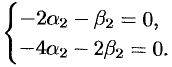
Положим 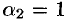 , тогда
, тогда 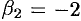 . Значит, корню
. Значит, корню 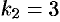 соответствуют частные решения:
соответствуют частные решения:
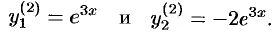
Общее решение исходной системы, согласно формуле (52.10), запишется в виде: 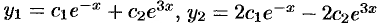 .
.
Случай 2. Корни характеристического уравнения различные, но среди них есть комплексные: 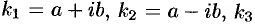 . Вид частных решений в этой ситуации определяют так же, как и в случае 1.
. Вид частных решений в этой ситуации определяют так же, как и в случае 1.
Замечание. Вместо полученных частных решений можно взять их линейные комбинации (п. 50.1, случай 3), применяя формулы Эйлера; в результате получим два действительных решения, содержащих функции вида 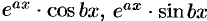 . Или, выделяя действительные и мнимые части в найденных комплексных частных решениях, получим два действительных частных решения (можно показать, что они тоже являются решениями уравнения). При этом понятно, что комплексно-сопряженный корень
. Или, выделяя действительные и мнимые части в найденных комплексных частных решениях, получим два действительных частных решения (можно показать, что они тоже являются решениями уравнения). При этом понятно, что комплексно-сопряженный корень 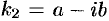 не даст новых линейно независимых действительных решений.
не даст новых линейно независимых действительных решений.
Пример №52.4.
Найти частное решение системы
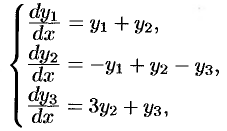
удовлетворяющее начальным условиям: 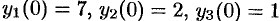 .
.
Решение:
Составляем и решаем характеристическое уравнение:
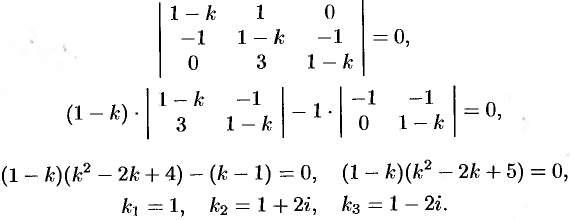
Для 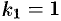 получаем:
получаем:
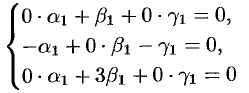
(см. (52.8)). Отсюда находим: 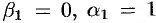 (положили),
(положили), 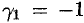 . Частное решение системы:
. Частное решение системы: 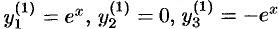 .
.
Для 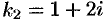 получаем (см. (52.8)):
получаем (см. (52.8)):
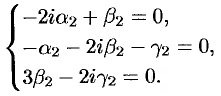
Отсюда находим: 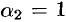 (положили),
(положили), 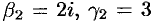 . Частное комплексное решение системы:
. Частное комплексное решение системы:
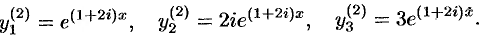
В найденных решениях выделим действительную 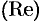 и мнимую
и мнимую 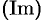 части:
части:
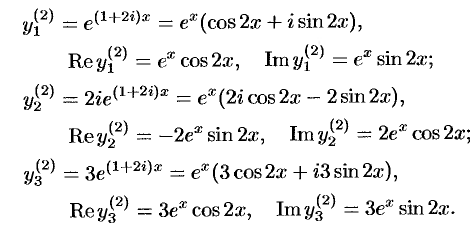
Как уже отмечено, корень 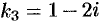 приведет к этим же самым решениям.
приведет к этим же самым решениям.
Таким образом, общее решение системы имеет вид
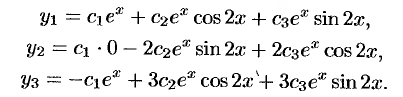
Выделим частное решение системы. При заданных начальных условиях получаем систему уравнений для определения постоянных 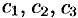 :
:
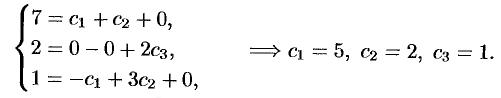
Следовательно, искомое частное решение имеет вид
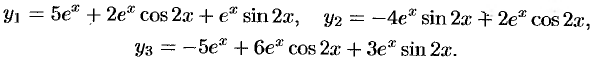
Случай 3. Характеристическое уравнение имеет корень 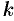 кратности
кратности 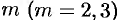 . Решение системы, соответствующее кратному корню, следует искать в виде:
. Решение системы, соответствующее кратному корню, следует искать в виде:
а) если 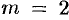 , то
, то 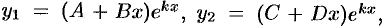
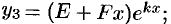
б) если 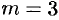 , то
, то 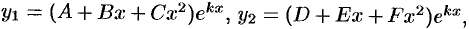
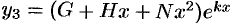
Это решение зависит от 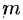 произвольных постоянных. Постоянные
произвольных постоянных. Постоянные 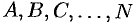 определяются методом неопределенных коэффициентов. Выразив все коэффициенты через
определяются методом неопределенных коэффициентов. Выразив все коэффициенты через 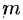 из них, полагаем поочередно один из них равным единице, а остальные равными нулю. Получим
из них, полагаем поочередно один из них равным единице, а остальные равными нулю. Получим 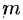 линейно независимых частных решений системы (52.6).
линейно независимых частных решений системы (52.6).
Пример №52.5.
Решить систему уравнений:
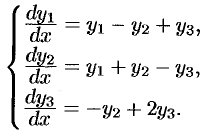
Решение:
Составляем и решаем характеристическое уравнение
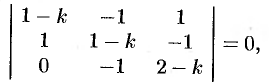
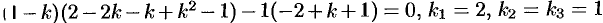 . Корню
. Корню 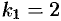 соответствует система (см. (52.8)):
соответствует система (см. (52.8)):
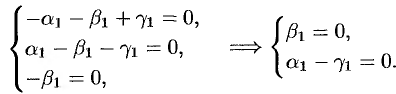
Полагая 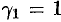 , находим
, находим 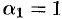 . Получаем одно частное решение исходной системы:
. Получаем одно частное решение исходной системы: 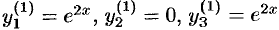 .
.
Двукратному корню 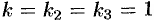 (
(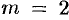 ) соответствует решение вида
) соответствует решение вида 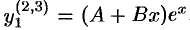 ,
, 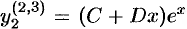 ,
, 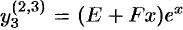 . Подставляем эти выражения (решения) в уравнения исходной системы:
. Подставляем эти выражения (решения) в уравнения исходной системы:
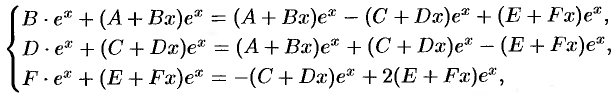
или, после сокращения на 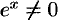 и группировки,
и группировки,
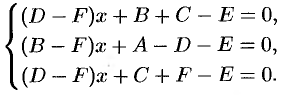
Эти равенства тождественно выполняются лишь в случае, когда
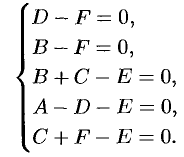
Выразим все коэффициенты через два из них (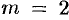 ), например через
), например через  и
и 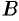 . Из второго уравнения имеем
. Из второго уравнения имеем 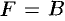 . Тогда, с учетом первого уравнения, получаем
. Тогда, с учетом первого уравнения, получаем 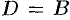 . Из четвертого уравнения находим
. Из четвертого уравнения находим 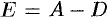 , т. е.
, т. е. 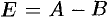 . Из третьего уравнения:
. Из третьего уравнения: 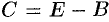 , т. е.
, т. е. 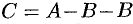 , или
, или 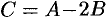 . Коэффициенты
. Коэффициенты  и
и 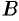 — произвольные.
— произвольные.
Полагая 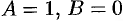 , находим:
, находим: 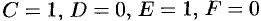 .
.
Полагая 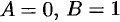 , находим:
, находим: 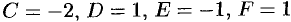 .
.
Получаем два линейно независимых частных решения, соответствующих двукратному корню 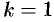 :
:
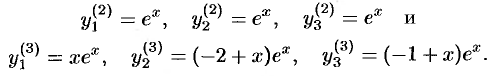
Записываем общее решение исходной системы:
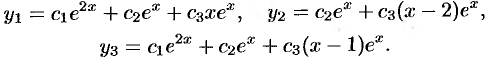
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:

