Оглавление:


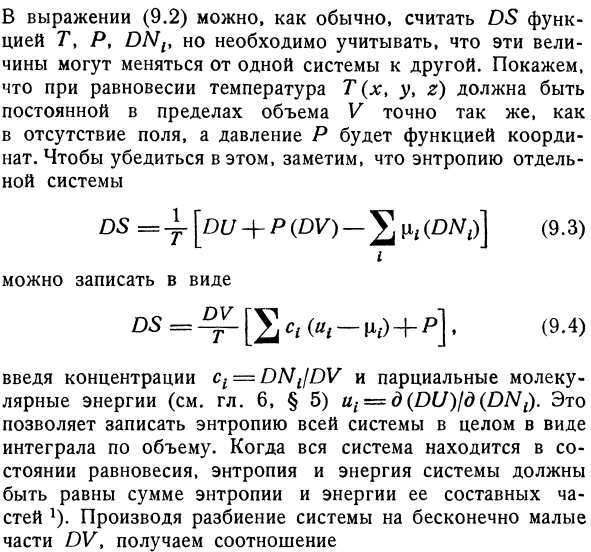






Системы во внешних полях. Гравитационное поле.
- Система внешнего поля Учитываются внешние силы и термодинамическое равновесие в поле изотермического воздуха. Обсуждается химическое равновесие в гравитационном поле. Гравитационное поле До сих пор мы считали, что система должна быть однородной или состоять хотя бы из ограниченного числа однородных частей(фаз).
Неоднородность нельзя игнорировать, если система находится в определенном поле, которое существенно изменяется от точки к точке. point. As типичный пример, гравитационное поле присутствует всегда, но его влияние в большинстве случаев незначительно, поэтому оно еще не рассматривалось.
Это предположение очевидно верно, если нет поля для внешних сил и внутренних напряжений, отличных от тех, которые вызваны изотропным давлением Людмила Фирмаль
Для исследования таких случаев необходимо опираться на локальное описание и учитывать такой небольшой объемный коэффициент, который позволяет с достаточной точностью рассматривать полевые константы в его пределах. Разделите весь объем на части В =%ДВ(9.1) Затем, через DU> DS и DNlt, мы получаем набор открытых термодинамических систем, которые находятся в контакте друг с другом, указывая внутреннюю энергию, энтропию и количество частиц в такой части соответственно.
Поскольку гравитационное поле можно считать постоянным в отдельной системе, оно явно не входит в термодинамическую идентичность. ТД.(ДС)= д(ду)+ др(ДВ)-2 м(ДНР)•(9-2) В Формуле (9.2) можно рассматривать DS как функцию 7 \ P, DNlt, как обычно, но нужно учитывать, что эти величины могут варьироваться от системы к системе system. In равновесное состояние, температура T (x, yt z) должна быть постоянной в объеме V, так как при отсутствии поля давление P является функцией coordinates. To подтвердите это, энтропия индивидуальной системы равна DS =±[DU + P (DV) — 2 фута(D ^ i)] (9.3) Я… Вы можете написать как ДС = в U С,(А,-[х + р].(9.4) Концентрация cl-DNJDV и введение парциальной молекулярной энергии (см. Главу 6,§ 5) ui = d(DU)ld (DNl).Это позволяет записать энтропию всей системы как интеграл от всего объема.
- Когда вся система находится в равновесии, энтропия и энергия системы должны быть равны сумме энтропии и энергии ее компонентов. С = Дж [/> +СС,(α,-JX у.)]. (9.5) В. Определите энтропию как функцию cL, ui% P и T объема V. Теперь вы можете применить условия общего равновесия (6С) ЭТВ <0,(9.6) Что касается флуктуаций, в которых энергия поддерживается постоянной, то она говорит, что энтропия должна быть максимизирована.
Здесь под словом «энергия» следует понимать совокупную энергию. Е в дополнение к внутренней энергии Это утверждение основано на нескольких assumptions. In другими словами, часть ДВ можно рассматривать как макроскопическую, то есть энергия поверхностного взаимодействия предполагается пренебрежимо малой по сравнению с объемной энергией. Потенциальная энергия системы во внешнем поле. Внутренняя энергия (9.7) (9.8) И = IdV 2 Кроме того, существует потенциальная энергия ^ МДМ — > JdVФ2 Где Φ (π, y) — гравитационный потенциал, а a / u ^-масса i-й частицы. Сумма обеих энергий (9.9)
В вариации bS должны остаться constant. In другими словами, энергия s должна быть минимальной по отношению к колебаниям константы S. поскольку в состоянии равновесия невозможно получить работу даже при перемещении определенного количества вещества в поле. Кроме того, колебания должны быть такими, чтобы общее количество каждого компонента не изменялось. (9.10) Давайте сначала напишем уравнение для вариации 65. 6С = Дж — {2К«, — Привет) б ’ л + пр(6У£ — 6к)] + ++(9.11) Не все вариации, представленные в (9.11), являются независимыми.
Из определения конкретной величины (см. Главы 6, раздел 4 и 5) видно, что вариации Li6T и δP связаны между собой следующими соотношениями: 2 кл 6ч, = −2 * А6 т + б р.(9.12)) Подставляя (9.11) вместо (9.12), вы можете увидеть, что 6P, bT и 6k. термин, который содержит /, выпал、 Система внешнего поля 183 Возьмем более простой вид 65 = J «и 7〜» З〜^ Б°1 + б » Р1 = BE = J dV ^ [(«i +ФФ+)+ c, urig]= 0, (9.13) 6N, = J DV 6CT = 0. Если применить множитель Лагранжа обычным способом, то получим 0 = 65-a6£- = J dV 2 {[ifLTB — » («/± fc] + Я… + — »)*».}. (9.14)
Эта связь будет идентична только в следующих случаях: Т =〜и Р / Т = — | — / Я / Ф (9.15) Константы в системе. = МФЛ> *(9.16) Как и прежде, температура остается постоянной. Давление не является постоянным. с, Φ(АГ, у, Z)= const и (9.17)
Таким образом, можно видеть, что в гравитационном поле координатно-независимой величиной является не химический потенциал, а химический потенциал плюс потенциальная энергия каждой молекулы. Людмила Фирмаль
Смотрите также:
| Недостижимость абсолютного нуля | Примеры |
| Постоянная давления пара | А. Некоторые физические константы |

