Оглавление:








Системы криволинейных координат. Координатные оси, линии и поверхности. Коэффициенты Ляме
- Задача 14. 1. При выражении в декартовых координатах выражаются условия, при которых криволинейная система координат ортогональна. Проверьте ортогональность сферической системы координат. Решение. 1 Общий случай. Определите положение точки m в пространстве в квадратурной декартовой системе. Координаты qlt qt, координаты x, y, z в системе координат кривизны по qa. Радиус-вектор точки m, взятый из начальной точки декартовой системы, равен r xi yj — — zk.
Координатной линией криволинейной системы координат является радиус-вектор r r при изменении только 1 криволинейной координаты qt. Я, ка 3 является ходжеграфом. Затем укажите направление координатных осей gj, yj, 7z1 orts fcx, е, и обратите внимание, что координатные оси ориентированы по касательной к координатным линиям в направлении увеличения координат. Д dqi 1 dr dqt Ноль Это равенство получается из того, что оба вектора dr dqt и d направлены по касательной годографа радиус-вектора в направлении, увеличивающем координату qh. 1 знаменатель равен коэффициенту Ляме Затем перепишите выражение 1 в виде Условия ортогональности криволинейной системы координат.
Изобразим груз в положении, смещенном относительно нуля па х вниз и предположим, что он движется в сторону возрастания х, т. Людмила Фирмаль
При задании уравнения 2 вместо 3 ДГ БГ йд 0 Ля Дайте 3 равенства 0- а dqt — Да. — и dhg ПКД ПКД dqt Выразить в форме Радиус-вектор через декартовы координаты запишем 4 dh. dh. ЗУ ЕС. ЗГ. ДГ д Я бы d4i собирает и бы 4 91 ЧГ ДХ ВХ Ду б йй, Чг чгдзз dqt ПКД ДХ ДХ, ду ду, ДГ ДГ йд,. Д ПКД Эти уравнения являются условиями для анализа ортогональности в криволинейной системе координат. 2 сферическая система координат см. Рисунок.
Координатная линия через начало координат d р с, 4 3 Ось g совпадает, это прямая линия, pro-. Точка m. Координатной линией 9 является окружность, нарисованная радиусом om. Ось 61 — касательная этой окружности, проведенная в точке m в направлении увеличения угла m. Координатная линия f — окружность параллельной окружности с радиусом r sin 9, а ось p — касательная этой окружности, проведенная в точке в направлении увеличения угла. Декартовы координаты могут быть представлены сферическими соотношениями Одновременные уравнения 5 Выпуск 14-i. Значения координат дхдх. дю. Добро пожаловать на наш сайт dh. — Я.
Поэтому сферическая система координат ортогональна. Задача 14. 2. Уравнение движения точки задается в цилиндрической системе координат. Знать формулу перехода от цилиндра Координаты т т Декарт х-П со ф, г-п грех Ф, з з Проверьте ортогональность цилиндрической системы координат. Найдите координатную линию, ось и координатную плоскость. Решение. Задача 14. 1 для решения аналитического условия ортогональности криволинейной системы координат 5 Я Р, А использование q3-z и зависимостей i — р с cos Р грех п п грех Р со ф 0 -п грех ф 0 р со ф 0 а 1 О.
Поэтому цилиндрическая система координат является orthogonal. It на рисунке показаны цилиндрические координатные оси, нарисованные в точках m p, , g. Координатными линиями в этом случае являются линия p — прямая линия am через точку m. const и z const линии — дуги окружности судна вдоль const и z const. Координатная плоскость цилиндрической системы координат выглядит следующим образом а поверхность bced цилиндра радиуса p с осью og, проходящей через заданную точку m Ось ОА и. . , г Плоскость abc через точку m Задача 14. 3. Эллиптические координаты-это координаты, связанные с уравнением ifo, m 2.
От 1 который p const Б проходящий через полуплоскость 0 точка m, phi const в горизонтальный. Константа на плоскости, называемой декартовыми координатами Проверка оси 1 Постоянное значение. Определяет границу изменения координаты липпика В Гц. И 1 представляет семейство фокальных эллипсов, а Формула 2 представляет семейство конфокальных гипербол рисунок а. Для a b найти коэффициент хромоты, координатную ортогональность системы. Решение.
- Докажем, что уравнения представляют собой семейство эллипсов и конфокальных эллипсов Хз 1. 3 Фактически фокусное расстояние эллипса 3 равно Полуоси a и b эллипса 1 равны соответственно Д А В1, б б Н1 5 Таким образом, фокусные расстояния эллипса 1 и 3 равны Равный х С Д2-52 А2-Б2 с 6 В этом случае, если Гц находится в следующем диапазоне, то уравнение 1 определяет эллипс. B к выпуску 14. 3. 6 м ОО. 7 b t, потому что это i 0 и дополнительно a2 t 0. Формула 2 определяет семейство гипербол включая эллипсы, если t a находится в следующем диапазоне — А8 ОК — БР 8 Кроме того, aa q4 0 и ba q4 0.
Тогда вы представляете полуось гиперболы 2 с d1, z Д a2 q2в — r na, фокусное расстояние гиперболы равно ci d a уа-Б2 с. Итак, если вы измените i j и m 2 в случае, обозначенном неравенствами 7 и x, вы получите семейство конфокальных эллипсов 1 и семейство конфокальных гипербол 2. 1. Одна кривая каждого семейства проходит через каждую точку плоскости. Поскольку эллипс пересекает конфокальную гиперболу в 4 точках симметрии, то для ясности необходимо дополнительно указать, в каком из 4 квадрантов будут расположены точки рассмотрения рис. Б. Координатная линия c1 const является эллипсом, а координатная линия m 2 const является конфокальной гиперболой.
Найти уравнение колебаний груза, если известно, что для деформации пружины на 1 см надо приложить к ней силу, модуль которой равен 14,4 г. Людмила Фирмаль
Приступаем к определению коэффициента хромоты. Когда мы решаем уравнение 1 и 2 вместе ХВ а ч1 а н 9 У заранее 8 П д б Р1 Коэффициент хромоты равен 41-р АИ ijihbi Н Изучите ортогональность системы. Условия анализа ортогональности эллиптической системы координат принимают следующий вид ДХ ДХ. Ду, ду г lc l lts dts — 15 Вычисляя эти частные производные, начиная с 11 и 12, и вводя их в 15, вы получаете после простого преобразования. 16 Система координат ортогональна. Это следует из известной характеристики касательной гиперболы-угол между радиусными векторами от фокуса до точки касательной делится пополам, а касательная эллипса одинаково наклонена к одному и тому же радиусному вектору рис. Б.
Примечание эллиптические координаты могут быть введены с помощью других dependencies. So например, переменные, связанные с Декартовыми координатами отношением и y х-cchgcosy, г cshgseny Также известный как эллиптические координаты, он может быть определен как функция эллиптических координат nc и t t, рассматриваемых в задаче. Координатные линии const является эллипса и координатной линии y const является конфокальные гиперболы с фокусным расстоянием. К задаче 14. 4. Задача 14. 4. Зависимость декартовых координат от тороидальных определяется по формуле х а pcosq costf, у а п потому что М sin, z с pslni, 1 a-oc const-отрезок прямой оа, вращающийся в плоскости cart декартовых координат см.
Рисунок. Положение любой точки m в пространстве определяется тремя тороидальными координатами. Азимутальный угол измеряется между осью ox и прямой oa, а 2 полярные координаты p и p расположены в плоскости zoa, проходящей через точку m. Проверьте ортогональность тороидальной системы координат, чтобы найти координатные линии, оси и поверхности. Solution. To подтвердив ортогональность тороидальной системы координат, построим аналитическое условие 14. 1 для задачи 5.
Если мы вычислим частные производные и введем их в 5 -потому что п п грех cos2 ф-п с cos Р грех e1n2p п греха, потому что 0, грех, грех, потому что а Кос грех -п sinфsitl ф т п Соэф СО8ф п Соэф О 0, -cosфcosф а рcosф sinф soeph 81pf а рcosф СО8ф 81Пф 0 0. Поэтому тороидальная система координат ортогональна. Приступим к определению координатных линий и осей. Пусть const и const находят координатную линию p. Это будет полупрямой sm, который является координатой p. Координатная линия может быть найдена, если p const и const. Это будет окружность с центром c и радиусом p в плоскости zoa. Касательная этой окружности направлена в сторону увеличения угла и становится координатной осью f.
Получить координатную линию, установив p const и const. It представляет собой окружность вокруг оси z точки r p51pf, радиус a pcoeff, в плоскости, параллельной оси xoy. Касательной этой окружности в точке m, которая направлена в сторону увеличения угла, является координатная ось f. Координатная плоскость выглядит так для p const-поверхность Тора, для const-поверхность конуса угла l 2- -для const-плоскость Зоа. Задача 14. 5. Уравнение, приведенное в вопросе 14. 4 1, определяет задние коэффициенты met тороидальных координат p, f и f, связанных с Декартовыми координатами см. Рисунок в вопросе 14. 4.
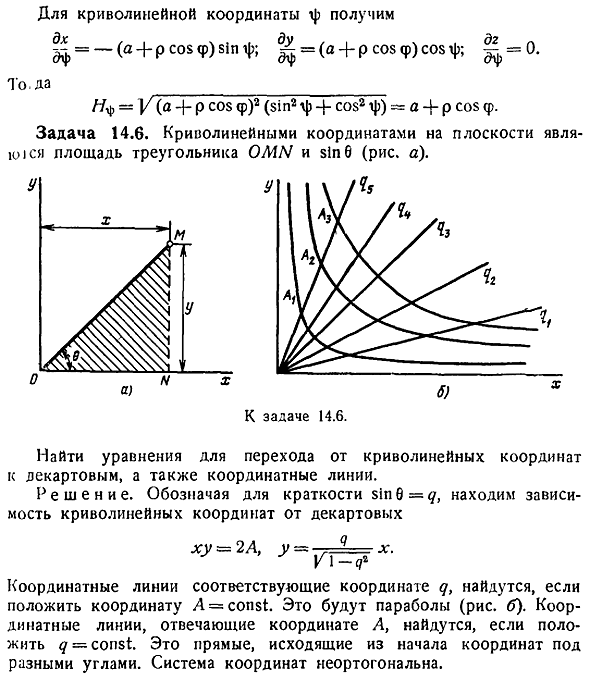
To найти коэффициент ламели, используя формулу 4 Подробнее о координата Кривой p ОТФ-Ф. Со И так оно и есть. Нр Уcos2фcos2ф cos2фsiп2ф sin2 р я О координате Кривой — rptfsoef — p 81pfz1pf, rsovf И так оно и есть. Р2 в sin2 Ф soe2f e1n2f sin2 Ф cos2 ф п. О координате Кривой б-ца pcosvjtos Тот. Да. У А Р соз СР грех cos2 а п с cos. Задача 14. 6.
Смотрите также:
Предмет теоретическая механика

