Оглавление:


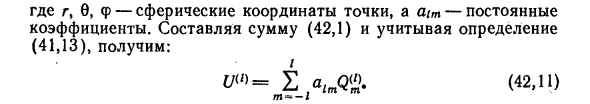

Система зарядов во внешнем поле
- Система зарядов во внешнем поле. Рассмотрим систему зарядов, находящуюся во внешнем элексе трическое поле. ea ^ (ra)> полная потенциальная энергия системы равна U = Y, eaV (ra). (42,1) а Выберем снова систему координат с началом внутри системы зарядов; …. Га — радиус-вектор заряда еа в этих координатах
Предположим, что внешнее поле слабо меняется на протяжении системы зарядов, т е является по отношению к этой системе квазиоднородным Тогда мы можем разложить энергию U в ряд по степеням га: и = * 7 (0) + и (1) + и (2) + … (42,2)
а где энергия приближается к началу координат Людмила Фирмаль
В этом разложении первый член есть Е / (0) = ^ о е е а, (42,3) . Второй член разложения С7 (1) = (град <р) 0 ^ е ар а. Введя напряженность и (1) = _ dE 0. (42.4) Квазиод- с точностью до рассмотренных членов, F = Е 0 ^ 2 еа + (град дЕ) 0.
Если полный заряд равен нулю, то первый член исчезает и тогда F = (dV) E, (42,5) т. е. сила определяется производственной напряженности полярности. K = ^ [r a -eaE 0] = [dE0], (42,6) т. е. определяется самой напряженностью поля.
- Рассмотрим две системы с равными нулю суммами зарядов в каждой из них и дипольными моментами ди и д 2, причем их взаимное расстояние велико по сравнению с их собственными размерами. Определим потенциальную энергию U их взаимодействия. Для этого можно рассматривать одну из этих систем как находящуюся в поле второе.
где Ei-поле первой системы. (40.8), находим где R-векторное расстояние между обеими станциями. Сумма расходов получи аналогичным образом: Здесь мы, как и в § 41, опустили индексы, указывающие номер заряда ;.
от потенциала берутся в начале координат Но потенциал Людмила Фирмаль
Значения вторых производных <р удовлетворяет уравнению Лапласа U = —d2Eb и = (did2) fl2-3 (diR) (d2R) R5 (42,7) (42,8) где R-вектор, направленный от диполя к заряду.
Следующий член разложения (42.1) равен д 2 <Р _ г & 2 <Р _ п дх2 ^ дхадхр Поэтому мы можем написать: или, окончательно, jj (2) = Рос? дУо 6 дхадхр (42,9) Общий член ряда (42.2) может быть выражен через опреде 2г-польные моменты (г) в ряд пошаровым функциям; общий вид такого разложения: ОО I J ———- lP (r) = J 2 rl (42,10) 1 = 0 м = -1 где г, 0, ip-сферические координаты точки, а а / ш-постоянные коэффициенты. Составляя сумму (42.1) и учитывая определение (41.13), получим г tf (0 = J 2 а (42Л1)
Смотрите также:
| Дипольный момент в физике | Постоянное магнитное поле |
| Мультипольные моменты в физике | Магнитный момент в физике |

