Оглавление:








Система сходящихся сил
- Одной из важных силовых систем, рассмотрим систему конвергентных force. Для системы этой силы необходимо рассмотреть ее простейшую форму и установить состояние равновесия. Система сходящихся сил или пучков сил это система сил, в которой линии действия пересекаются в 1 точке центре пучка. Система сходящихся сил может быть пространственно и плоской, то есть располагаться в одной плоскости. Уменьшите совместные усилия. Рассмотрим общий случай пространственной системы сходящихся сил.
Поскольку сила, действующая на твердое тело, является движущимся вектором, то сила tF F2,…, ФН можно предположить применяться до 1 точки центра пучка рис. 12. Примените аксиому параллелограмма к первым 2 силам балок F и F2, заменив их на 1 равнодействующую силу Rl2 рис. 13. 12 = 1 + 2 Затем, по правилам параллелограмма, сложите силы Rl2 и F3 и получите результат. И так далее.
Из — за тяжелого твердого тела,вращающегося вокруг неподвижной точки,в трех случаях была задана система первого интеграла дифференциальных уравнений,из которой во времени были сформированы неизвестные углы Эйлера. Людмила Фирмаль
Продолжается процесс векторного сложения сил против всех n сил л = 12 + + + з 1 я = 1. Таким образом, системе из N сходящихся сил соответствует 1 сила R . Это результат системы сил. Процесс последовательного применения правил параллелограмма к силе, или сложение его вектора, строит силовой полигон из заданного Force. In силовой полигон, конец одной силы выступает как начало силы другой рис. 14.Равнодействующая сила H силового многоугольника соединяет начало Первой силы и конец последней силы. То есть в общем случае рисуется открытый замкнутый силовой полигон. Силы силы внутри многоугольника могут быть представлены в любом порядке.
Это изменяет форму силового многоугольника и не изменяет closure. As в результате результирующая сила не изменяется. Для пространственной системы сходящихся сил силовой многоугольник является пространственной фигурой, и он является плоским flat. In в случае плоской системы сходящихся сил результирующая сила может быть определена графически путем создания многоугольника задней силы в масштабе, выбранном для force. In космическая система сходящихся сил, необходимо построить силовой полигон из стержня в пространство. Поэтому, как правило, система сходящихся сил Дело сводится к 1 силе равноденствию Системы этой силы. Заключительная сила мулти Треугольник построенный с силой системы У нас есть.
Линия действия равнодействующей силы проходит через центр балки параллельно замкнутому силовому полигону. Для аналитического определения результирующих сил необходимо выбрать систему ортогональных координатных осей и использовать известную теорему из геометрии о том, что проекция любого многоугольника на любую ось равна сумме проекций составляющих его сторон на одну и ту же ось. Потому что результирующая сила R является замкнутым силовым полигоном, или векторной суммой сил 1 я 1 Если вы проецируете вектор, векторы которого равны на прямоугольных координатных осях в соответствии с теоремой проекции замыкания, вы получаете f Fu. Ры = я Фий Р = Физз.
Из проекции определяют Косинус модуля результирующей силы и угол с координатными осями, согласно формуле n = 7 i 2+ i 2+ i: 2 = q e F a 2+ f 4. Три в COS х, = A 8 Лу, Lu = со Ф, Аз = Дж с. 4 в уравнении 3 определяется модуль результирующей силы, поэтому знак плюс всегда берется перед квадратным корнем. Для плоской системы сходящихся сил, когда 1 из осей координат обычно Oz выбран перпендикулярно силе, каждая сила луча дает проекцию на эту ось. Так как она равна нулю, то проекция силы, синтезированной на этой оси, равна нулю.
Условия равновесия системы сходящихся сил Чтобы уравновесить систему сходящихся сил, приложенных к твердому телу, замыкание силового многоугольника, представляющего результирующую силу, должно быть точечным. То есть конец последней силы многоугольника должен совпадать с началом Первой силы. Такой силовой полигон называется замкнутым рис. 15.Получены условия равновесия сходящихся сил геометрических фигур: для равновесия системы сходящихся сил, приложенных к твердым телам, достаточно замкнуть силовые полигоны, составленные из них forces. In в случае 3 сходящихся сил, находящихся в равновесии, необходимо замкнуть треугольник сил, состоящий из 3 forces.
To для определения неизвестной силы, находящейся в равновесии, более желательно использовать равновесное состояние системы сходящихся сил в аналитической форме. Система сходящихся сил из за нахождения в равновесии Если результирующая сила должна быть равна нулю силовой полигон замкнут, то радикальная Формула 3, состоящая из суммы положительных величин, будет равна нулю. Таким образом, каждый квадратный Значение радикального выражения, а следовательно и сама сумма, равно нулю. Получаем условие равновесия пространственной системы в ванитивной форме сходящейся силы. ZFte = 0 F , 0 Fiz = 0, 5 = я Я = Я Я = я т. е.
Для равновесия пространственной системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы сумма проекций сил для каждой из 3 х прямоугольных осей была равна нулю. Для плоской системы сходящихся сил 1 обычно Oz координатных осей выбирается перпендикулярно силе, в то время как другие 2 оси выбираются соответственно плоскости силы. Тогда 3 е условие 5 от идентичности Fjz = 0.Если вы отбросите его, это будет 1 = 1. F = 0 Fjy = 0, 6 я = я я = я То есть для равновесия плоской системы сходящихся сил, действующих на твердое тело, необходимо и достаточно, чтобы сумма проекций этих сил для каждой из 2 х прямоугольных координатных осей в плоскости силы была равна нулю.
Проецирование сил на координатные оси Учитывая силу F, проекция на прямоугольные координатные оси вычисляется как Форекс = Г Т = Feos Ф АКС Ф = Ф. = Feos ф г ФЗ = Ф Р = объекты первого класса Ф, з. Где i, j и F единичные векторы, направленные вдоль осей. Угол силы и косинус осей координат удовлетворяют условию cos2 Ф АКС + cos2 Ф, Ас + cos2 Ф, з =1.Из 3 углов только 2 являются независимыми. При проецировании силы на прямоугольную координатную ось также рекомендуется использовать 2 угла. Из за этого сила сначала разлагается на 2 взаимно перпендикулярных компонента.
- Одна из них параллельна любой координатной оси например, Oz , а другая находится в координатной плоскости двух других осей в данном случае координатной плоскости Ohu рис.16. Возьми Ф = А + Пока Когда вы проецируете вектор осей is, он выглядит следующим образом: Форекс = Fsinacos 0 ФГ = Fsinacos 0 Fz = Fcos a, потому что Fxy = ФСИНа. При проектировании использовались только 2 угла a и 0. Векторные значения Fx, F, Fz называются компонентами силы F вдоль осей координат. Скалярная величина Fx, F F Z, является проекцией силы F на координатные оси. Поэтому сила, приложенная к осям, обычно проецируется в фазе 2.Во первых, он проецируется на координатную плоскость 1 оси и 2 других осей.
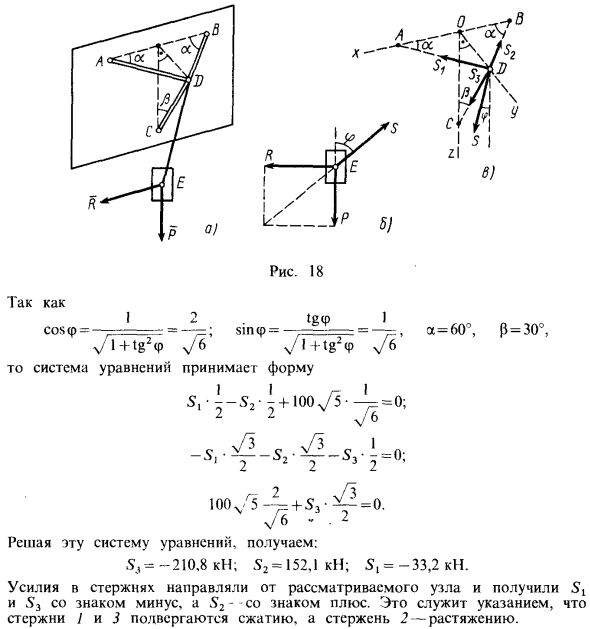
Проекция силы на плоскость является вектором. Этот вектор проецируется на оси в плоскости. Пример 1.Кран с вертикальной осью вращения АВ состоит из неподвижного стержня с шарниром. Ось крана фиксируется с помощью упорных подшипников а и в рис.17, а. Принимая во внимание общий вес штанги и крана, определите силу реакции упорного подшипника и подшипника, штанги A, I и штанги A, а также угол ai, a2 az, если известны размеры a, I. Стержни 2 и 5 расположены горизонтально. Кран, используя кабель CD, под действием силы тяжести удерживает груз R. Solution.
Теорема об изменении кинетического момента системы при относительном движении относительно центра масс рассматривает относительное движение системы только относительно системы координат и не учитывает относительное движение системы. Людмила Фирмаль
Ввиду того, что кран является сплошным, он освобождается от муфты, которая является упорным подшипником и подшипником, и заменяет ее силой реакции муфты. Сила реакции подшипника цилиндрический шарнир перпендикулярна валу. Направление силы реакции упорного подшипника заранее не известно, поэтому его необходимо определить. Действуют 3 силы на весь кран в равновесии: р, ра, РБ рис. 17.6.Линии действия этих сил должны пересекаться в 1 точке. То есть линия действия силы Jal должна проходить через точку K, в которой пересекаются линии действия силы P и RB. 3 силы также должны образовывать замкнутый силовой треугольник.
Поместите силу P на выбранную шкалу и проведите линию, параллельную силе Ra и Rb, до ее начала и end. In в полученном силовом треугольнике 3 силы направлены одна за другой рис. 17, в. Из полученного прямоугольного треугольника РА= , ТФБ = Ptga. потому что Из геометрического треугольника ABK вы получаете A ЛI коза= , ТГА=. г Н2 + Л2 ч Для определения силы тяг 1 и 2 применяют метод разрезания узлов. Для этого рассмотрим равновесие отдельного шарнира или узла С. сила Р действует через силы реакции этого троса и стержней 1 и 2.Сила реакции стержня на узлы должна быть направлена вдоль стержня, так как никакая другая сила не действует на эти стержни между их шарнирами.
Стержень закреплен на шарнирах. При необходимости увеличить число одинаковых числовых обозначений силы, указать силу реакции стержня от узлов рис. 17, г, согласиться поставить знак вектора силы на рисунке НС После выбора координатных осей в точке с настройте условие равновесия плоской системы сходящейся силы, действующей на узел С. Исправить = 0, Фий = 0. Эти условия в рассматриваемом случае принимают форму проекции на ось. Х С2 + Slcoszl = К г п + с Сина= 0.
Из полученного уравнения получаем следующее: Знак. Это указывает на то, что направление этой силы противоположно принятому направлению. По направлению к узлу. Рассматривая равновесие отдельных стержней 1, мы уверены, что только 2 силы со стороны узлов С и Е будут действовать на стержень. Эти силы должны быть равны по абсолютной величине и противоположны по направлению в равновесии. Узел C действует на стержень I с силой s в противоположном направлении к силе, действующей на стержень в узле E рис.17.6. таким образом, если принять во внимание равновесие узла C, то можно увидеть, что если величина S отрицательна, то стержень сжимается. S2 теперь является плюсом.
Поэтому стержень 2 будет находиться в напряжении. Поскольку узел с имеет 3 силы, действующие на него, необходимо сформировать замкнутый силовой треугольник. Построение треугольника сил должно начинаться с известной силы P и проходить через край линии, параллельной силе реакции стержня, величина которой неизвестна рис.17, f .Из треугольника сил можно определить силы S1 и S2. Из уравнения равновесия или треугольника сил можно определить только 2 неизвестные силы. Поэтому для дальнейшего решения задачи необходимо учитывать равновесие узлов, в которых действуют не более 2 неизвестных сил. Таким узлом является узел L. 3 неизвестная сила действует на узел.
Если мы рассмотрим равновесие узла L, то снова направим силу реакции стержня из этого узла, независимо от ранее полученных знаков для стержня рис. 17, г. в уравнении равновесия известная сила S2 должна быть заменена ранее перенесенным знаком плюс. Условие равновесия силы, действующей на узловую точку L, принимает вид: х С2 4 потому что С3 А2 С4 А3 со = 0 г грех 4 С3 А2 С4 грех А3 = 0 Sina2 S2tga3 Из этих выражений следует, что S4 53 S3 — sma3 cosa2 tga24 tga3 Если вы присваиваете значение 3, полученное выражению в S4, вы получаете: S2tga2tga3 sina3 с iga24 tga3 Группа С3 С2 с положительным отрицательным. Поэтому стержень сжимается. Усилие S4 является положительным.
Таким образом, стержень растягивается. Для узла L можно также решить задачу построения замкнутого силового треугольника и нахождения геометрически неизвестных сил. Пример 2.Груз с силой тяжести P = 200 кН устанавливается на шарнире D с помощью троса. Шарнир D крепится на вертикальной стене с помощью 3 стержней, 2 из которых используются для горизонтальных поверхностей, а 3 й для шарниров. Сопротивление нагрузки ветром L = 100kN находится на уровне и параллельно стене. для a = 60r, p = 30 определим натяжение троса и силу тяги, принимая во внимание невесомость штанги рис.18, а. Решение.
На нагрузку Е в равновесном состоянии оказывает влияние система из 3 сходящихся сил на вертикальной плоскости, параллельной стенке. Это напряжение S, направленное на гравитацию P, сопротивление R и кабель S рис.18.6.Сила S должна уравновешивать силу P и результаты H. И так оно и есть. 5 = JP2 + R2 = 1 00h 5 кн. Потому что силы P и R вертикальны. Сила S создает угол p относительно вертикали. Р 1 ТГ Р= =. 3. Рассмотрим действие натяжения троса, равное S рис. 18, В, при равновесии шарнира D, где силы реакции стержней S1, S2 и S3 направлены вдоль стержня. Существует пространственная система сходящихся сил, равновесные условия которой принимают вид: Fix = 0, к 1 = 0.
В этом случае для выбранных осей существуют: Cosa4 ы х СЖ коза С2 апельсин Р = 0 Дж с Сина Сина С2 С3 sin0 = о z ф4 53cos 0 = 0 из 5. Восемнадцать С 1 2 in 8 1 Ч. В. , , вл + tgcp В6 7,+ t82 стр. 76 Система уравнений принимает вид а = 60 S, S2 + 100 5 D 0 2 В6 2 10 5— + 3 = 0 V6 Когда вы решаете эту систему уравнений, она выглядит так: , = 210,8 кн 2 = 152,1 кн, = 33,2 кн. Сила в стержне направлена от рассматриваемого узла и получена, причем 3 со знаком минус, а S2 со знаком плюс.
Смотрите также:
Теоретическая механика — задачи с решением и примерами
| Теорема о переносе силы вдоль линии действия | Приведение к равнодействующей силе |
| Теорема о трех силах | Условия равновесия системы сходящихся сил |
Если вам потребуется заказать теоретическую механику вы всегда можете написать мне в whatsapp.

