Оглавление:

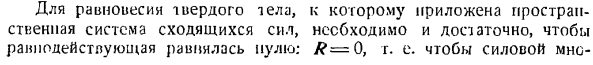


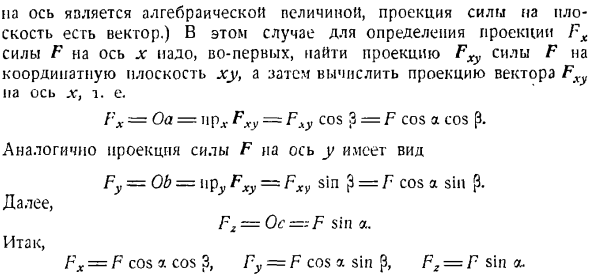











Система сходящихся сил
- Система сил сближения В Главе 1§ 1 рассматривалась плоская система сходящихся сил. Пространственная система сходящихся сил, такая как плоскость, также сводится к результирующей самости. Синтетическое R пространственной системы сходящихся сил также применяется к пересечению линий действия компонентов, эти силы являются задней стороной силового многоугольника, состоящего из R.
То есть пространственная линия нарушена. Проекция результирующей силы R на оси декартовых координат x, y, z равна сумме проекций составляющих сил на соответствующие оси. Р= х F ** ры =£/ в = £Б(2 *) к = I ЗДК ^ Л К-Я Результаты модуля/?
В отличие от соответствующей плоской задачи, силовой полигон не является плоским. Людмила Фирмаль
Равный Направляющий Косинус задается формулой: Потому что(Х’, р), соѕ (/>)=, потому что (>Г>)=. (4 *) Добавьте новый ic к средней точке и предположите, что стержень растянут (ориентирован Т. И Ти и Принудительно до 1 л. Они были названы 7-м примером направления реакции связывания, который рассматривался в начале книги.
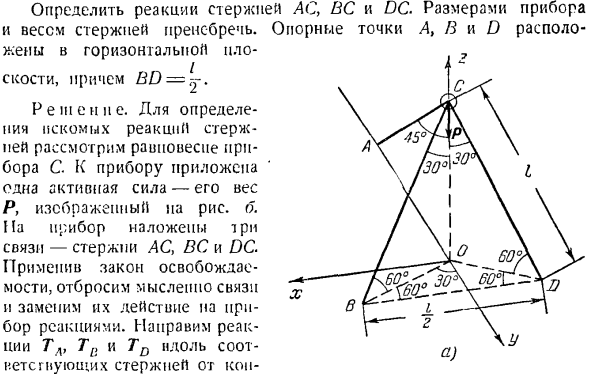
Теперь мы можем изучать равновесие устройства как свободное твердое равновесие под действием пространственной системы из 4 сходящихся сил: P, TA, Tn, TD. In в этом случае необходимо создать 3 проекционных уравнения на оси декартовых координат. Число алгебраических неизвестных Если она равна 3 (T, T и TD), то задача определяется статически.
- Проведите ось x вдоль линии действия силы P, а на пересечении горизонтальной плоскости и оси z, где расположены точки A, B, D, выберите начало координат O. ориентируйте оси x и y этой плоскости параллельно и перпендикулярно вспомогательной линии BD соответственно. Используйте TD Поскольку угол между линией действия и осью l: и y этих сил неизвестен, построение уравнений равновесия создает трудности при проектировании сил Tn и Tn на оси x и y axes.
By таким образом, сначала силы Ti и TD проецируются на плоскость xy, а затем эти проекции TPhu и TDx проецируются на»ось x и ось y».Силовой модуль tnhu и тд * г Рави Тху = ТВ соѕ 60°, TDXy = тд Косинус 60°. (Я) векторные конструкции Tllxy и Thnu на осях x и y определяют угол между линиями действия этих сил и осями x и Y. Из OVS и ODC прямоугольного треугольника, OV = = OD = l-sin 30°= / / 2, где / — длина каждого стержня.
Таким образом, угол, под которым образуются ОБ и ось, равен СО0. Людмила Фирмаль
Треугольник OBD является равносторонним треугольником, поскольку по условиям BD также равен. приступим к составлению уравнений проекции сил на ось X. проекция сил P и TA на ось x равна нулю(сила P перпендикулярна оси x, а TA находится в плоскости yz, перпендикулярной этой оси).для вычисления проекции сил Tn и Td векторы T {} xy и Tnu должны быть проецированы на ось X. Эти проекции равны соответственно: — COS 60°и-TDxy cos 60°.
Таким образом, форма уравнения проекции на ось x имеет вид £Fkx = TRxy cos 60—TDXV cos 60°= 0、 Учитывая равенство(1), запишем: 2 Fkx = 7ocos2 60° — TD cos2 60°=0.(2) при проектировании сил на ось Y, в дополнение к соответствующей проекции Т -} и ТДТ, в дополнение к Tnhu соѕ 30°и TDxy соѕ 30°, половина проекции та Т сила равна Т Т соз 45°(сила Р перпендикулярна оси Y).
Так, проекция уравнения на ось Y записывается в виде: £Fby = TRxy cos 30° — j-TDxy cos 30° — TA cos 45°= 0 Принимая во внимание равенство (1), получаем следующее: v rby = TB cos 60°cos 30°TD cos 60°cos 30° — TA cos 45°= 0 (3) Легко создать уравнение проекции для оси z, потому что угол, образованный линией действия и осью z каждой силы, известен. 23Fkg = — P-T cos 45° — TB cos 45° — TD cos 30°=0.(4) Осталось решить систему уравнений(2) — (4).
Из Уравнения (2) Следует, Что Ta = Tn. Вычитая (3) из (4) и считая, что Tv = Tn、 TB = TD = s-9 V3 P = −0.38 P. получено Подглвпв 1/2. Значения Tv и TD в уравнении (3), TA =-0.47 P = −0.47 P、 Знак минус в ответе указывает на то, что найденная сила не ориентирована, как показано на рисунке. 6, но как раз наоборот. Это означает, что АС, HC и стержней постоянного тока подвергаются сжатию, а не напряжение.
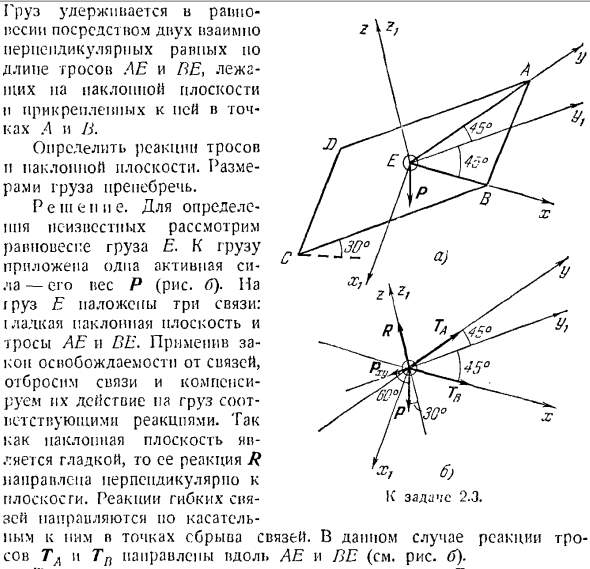
Задача 2.3.Гладкая прямоугольная наклонная плоскость ABCD с йодом, расположенная под углом 30°к горизонту, имеет нагрузку E весом P Точки загрузки.4 и B сбалансированы 2 взаимно перпендикулярными глухими кабелями длины AE и на angled N прикрепленном к блоку. Определите реакцию троса и наклонной плоскости. Игнорируйте размер нагрузки. The solution.
To определим неизвестные, рассмотрим равновесие нагрузки E. нагрузка£имеет 1 активную силу, т. е. массу P(рис.6).На груз е накладываются 3 муфты: (пренебрегая наклонной плоскостью ZY и кабелем AE и BE. Реакции гибкой связи ориентированы, но тангенциальны к ним в точке резания связи.
Здесь равновесие нагрузки Е можно рассматривать как равновесие свободного твердого тела под действием 4 сил: Р, та, Т№, которые образуют пространственную систему сходящихся сил. Эта система позволяет создать 3 уравнения равновесия. Число алгебраических неизвестных также равно * jpCM(Ra, T и 7’l), поэтому задача определяется статически.
Учитывая, что тросы AE и BE, а следовательно, силы T и Tn перпендикулярны друг другу, оси x и y направлены вдоль линий действия этих сил, а ось z перпендикулярна этой плоскости, то есть вдоль линии действия силы R. При таком осевом выборе проекционные координаты будуговых сил R, TA и Tn являются величиной нуля или соответствующей force.
It необходимо преодолеть некоторые трудности только при проектировании силы P, так как неизвестно, какой угол образует линия действия силы P на осях je и y. So, предварительно проецируя силу P на плоскость xy, найдите вектор Pxu (проекция вектора на плоскость также является вектором), а затем проецируйте Pxu на ось x и ось Y.
Модуль вектора » Пху » — это ПХ = П Косинус 60°. (1) Приступим к построению уравнений равновесия пространственной системы сил сходимости. Для этого, сумма проекций всех сил на оси декартовых координат Х, Y, R, должна быть равна нулю. Форма этих уравнений для этой задачи является 2 = РХ + Р * — налог + м » х = о、 £ГКУ = Пы ры + Тэй-Джей — сайт twu = о、 X = Pz Rz-1-TAg + TBg = 0
После замены значений проекции силы: РХ = — данные Косинус 45°, ГХ = 0, Телекса = 0, данные = Tjp ПБ = — данные грех 45°, ры = 0, Тай = та> ТБИ = 0, Р2 = — Р соѕ 30°, РЗ = Р } раз — = о, ТВГ = 0、 Эти уравнения принимают вид Rhu cos 45°TV = 0,(2) Несется 45°+ TA = 0, (3) P cos 30°+ H =0.(4) Осталось решить систему уравнений(2) — (4), учитывая равенство (1), Определить неизвестные.
Выйти. ТП = 7Д = — Пху-Р = 0.3 5П,/? = 1 ^ p = 0,87 A. При составлении уравнений равновесия пришлось столкнуться с трудностями при проектировании силы P на оси x: u, поскольку ранее необходимо было проектировать P в плоскости xy. Этих проблем можно избежать, направляя ось Y-вдоль 2-isorial осью угол а-ЕВ, ось Z вдоль оси Z, а ось Y-вдоль оси X.
Теперь, поскольку появляется силы Р в плоскости комфорта постояльцев во всех номерах, оси X{ый з { pXi-0, RU1 = — Pcos 60°, P2i = — Pcos 30°. Ыыы =- уравнение равновесия нагрузки в проекции на ось xy yy 2}описывается следующим образом: £FkXl = — TA cos 45°+ Tn cos 45°= 0, (5) 2Fkyi = — П соѕ 60° — й-ТА Косинус 45°г. в. в COS 45°= 0, (6) в / ч,, — я ведь 30°+ Я =0.(7)
Сравним систему уравнений(2) — (4) и (5) — (7).Учитывая эквивалентность уравнений(4) и(7), составление уравнений(о)и (6) является более простым и, следовательно, более желательным, чем составление уравнений (2) и (3).Объем вычислений при решении систем (2)-(4) и(5) — (7) примерно одинаков, поэтому выбор осей x] 7 y\, zj является более целесообразным. Я…
В. Мещерский рекомендует решать следующие задачи «сборника задач теоретической механики» начиная с 1950-х годов:212 216, 217, 220 В случае жесткого равновесия, в котором применяется пространственная система сил сходимости, необходимо и достаточно, чтобы результат был равен нулю. #= 0, то есть сила- Гон был closed. In кроме того, форма уравнения равновесия равна=0.(5 ) А-я.
Если алгебраические неизвестные равны 3, то задача определяется статически(не предполагая, что все силы находятся на 1 прямой или на одной плоскости).таким образом, если вы знаете направление всех сил, вы можете определить 3 силовых модуля. Для решения задачи равновесия твердых тел под воздействием пространства
В системе сил сближения необходимо встретить первые 4 точки, которые обозначены в начале k и r, а также a и t. 15.После этого: 5) убедитесь, что задача определена статически, то есть алгебраические неизвестные равны до 3. 6) осевая система декартовых координат. выберите s, Y и-G. 7) в проекции на ось декартовых координат создайте уравнение твердого равновесия (5). —1 Рисунок 2.1. 8) решить систему уравнений полученных результатов, то есть определить неизвестные величины.
При поиске синтетической пространственной системы сил сходимости, после завершения первых 6 точек, необходимо определить проекции Rxi Ry, Rz, используя формулу (2), и вычислить модуль синтетического R и косинус направления по формуле (3), (4*). Рекомендуется, чтобы начало координат декартовых осей координат выбиралось на пересечении рабочих линий составляющих сил.
Координаты малых должны быть направлены параллельно или перпендикулярно большинству этих сил. Проекция силы на координатные оси, например, сила F на оси x, угол между осью x и линией действия силы может быть неизвестен, но с учетом угла a и угла p, образованного силой F и координатной плоскостью xy (рис. 2.1) между проекцией оси x и линией действия силы
Координатная плоскость xy. (Во время проецирования силы, не забывайте об этом В этом случае для определения проективной Fx силы F оси x сначала находят проективную Fxy силы F координатной плоскости xy, а затем вычисляют проекцию вектора Fxy оси x, 1.е. С GX = ОА = Ирл. FXY = Fxy cos? — Ф потому что потому что С.
Аналогично, проекция силы F на ось Y имеет вид: = Обь = пр Fxy-Fxy за грех Е = F потому что грех п Следующий Ф2-ОЦ-Ф грех. Так… Форекс = Ф, потому что значение COS 3, ФГ = Ф, потому что грех-п, ФЗ = Ф грех. необходимо смешать состав Силы Света с понятием f Ic, проекцией силы на ось (рис. 9.2).
Компонент силы представляет собой вектор, равный произведению проекции соответствующей силы на единичный вектор проекции. Форекс = ФДЖ, ФГ=ФГ]、 Ф2 = ФЗК. Разложение силы F на единичный вектор оси декартовых координат、 Ф = РЖ-(- FyJ — Джей-диф- Если проекция силы на ось отрицательная, то соответствующая составляющая силы направлена только в противоположную сторону от положительного направления этой оси.
Задача 2.1.Определите результирующую пространственную систему сил сближения, показанную на рисунке. Мощность F3 и Fz находятся в плоскости xy, мощность Fv — в плоскости y, а мощность F4-в плоскости xz. / 71 = 2 n, F * = F3 = 4 RA = 6 n. Решение. Полученный R можно определить как заднюю сторону силового многоугольника, построенного на основе Fit Fb f4 и Fit. То есть R = Fx -] rF.1 — {- F2 — {- Fi.
Однако, поскольку этот полигон представляет собой пространственную пунктирную линию, прямое определение модуля и направления вектора R требует применения сложных методов построения моделей или начертательной геометрии. Эта проблема может быть решена гораздо проще с помощью проекции method. As известно, что проекция результирующего R определяется по формуле (2*).
В этом случае форма этих выражений Rx = — P \ x-G F * x + 1: 2x исправить » Ры = ф \ г-г ф * г-ый〜Б 1 ’\ г•РЗ = Ф \ с «ГFlzН〜» в Ф-Фу ФБ F3 и интернет на ОСН л*, У, 2: вычислить проекции силы. /:,.v = 0, FXy = F, cos 60°, F1z = F, cos 30°; Исправить= Фи Косинус 30°, Фив =-Т7 * потому что 00°, Фу = 0; ф ^ = Косинус 45°ФЗ, F3v = Ф \ Косинус 45°, Фу = 0; Взлетел = Ф \ Косинус 45°. Фу == Ф4, потому что 4 5°, Р1 в = 0、
Если вы присвоите эти значения выражению(I), оно будет выглядеть следующим образом: = в COS 30°+Рзcos 46 ° + Фи Косинус 45°, РВ = Ф}, потому что «0 ° -Ф3, потому что Г (К ° −1″Г3cos 45°, РЗ = потому что О0 ° Ф \ cos4r)°、 (!) Теперь, используя число, указанное в условии, найдите следующее: РХ = 10,5 Н, ры = 1, 82 я, РЗ = 5.9 ° С.
Теперь вы можете легко найти полученный модуль R R =] / R%^ rR ^ — Rl = 12.3 n и его индукционный Косинус: cos(x, P)= — * −0.86> потому что(г, р)= уу-0,1 о、 потому что(гг /?)= 7 ^ = 0,57、 01 здесь Как только вы знаете модуль и направление результирующего R, вы можете представить его в системе координат оси X.
Задача 2.2. Дозатор Р установлен на штативе.3 стержня AC, BC, PS имеют одинаковую длину и соединены шарниром C(рисунок A).Образуются стебли солнца и постоянного тока! С углом 30°вертикальным, и углом штанги АК 45°. К задаче 2.1.
Смотрите также:
Предмет теоретическая механика
| Равновесие тел при наличии трения | Произвольная пространственная система сил |
| Графическая статистика и методы расчета ферм | Центр тяжести |

