Синтез корректирующих устройств по логарифмическим амплитудно-частотным характеристикам

Оглавление:

Это изображение имеет пустой атрибут alt; его имя файла - image-10-1.png

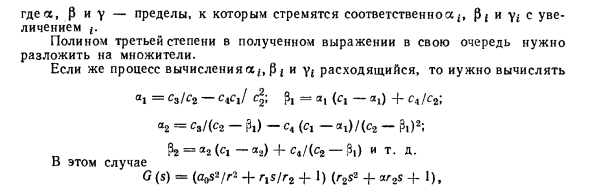
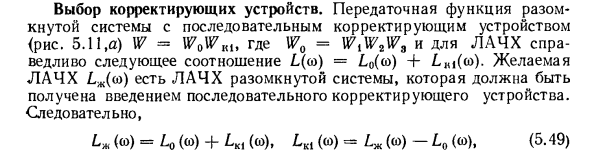
Синтез корректирующих устройств по логарифмическим амплитудно-частотным характеристикам

Синтез модифицированных устройств с логарифмическими амплитудно-частотными характеристиками Давайте рассмотрим другой способ синтеза корректирующего устройства. Он был разработан в мельчайших деталях и используется в широком спектре приложений. Давайте посмотрим на передаточную функцию неизмененной части системы W0 ($) «V? O (*) / [sv’Qo (s)], Где R0 (s) \ Q0 (s) — многочлен от s со свободным членом, равным 1. vo является постоянной величиной. Система должна иметь статический порядок v-ro, иметь качественный коэффициент k, превышать значение o и время настройки меньше tP. Такой набор требований часто предъявляется к системам отслеживания.

Статистика v и значения коэффициента качества / g выбираются на основе точности, необходимой для стационарного регулирования. Выбор показателей качества переходного процесса (превышение и время регулирования ТВ) обеспечивает необходимую скорость и динамическую точность системы. В некоторых случаях при начальном несоответствии g0 регулируемое ускорение координат не должно превышать допуск w. Такое ограничение необходимо, например, в механических системах, где контролируемой координатой является смещение.

Не допускайте возникновения недопустимых перегрузок (механических, электрических и т. Д.) На регулируемых объектах и исполнительных элементах. Людмила Фирмаль

Если статистический порядок v0 инвариантной части системы меньше v, легко подтвердить, что элемент преобразования усиления требует (v-v0) интегрированных связей. Также легко определить требуемое значение коэффициента передачи элемента усиления преобразования, которое равно k / k0. Поэтому задача сводится к синтезу корректирующих устройств, которые обеспечивают необходимые динамические характеристики системы.

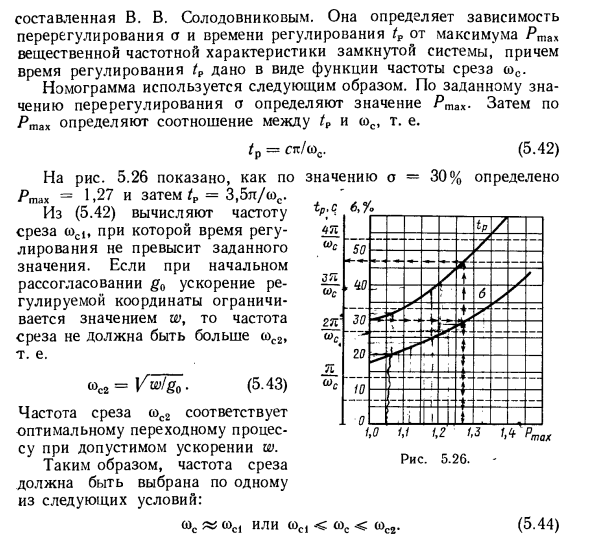
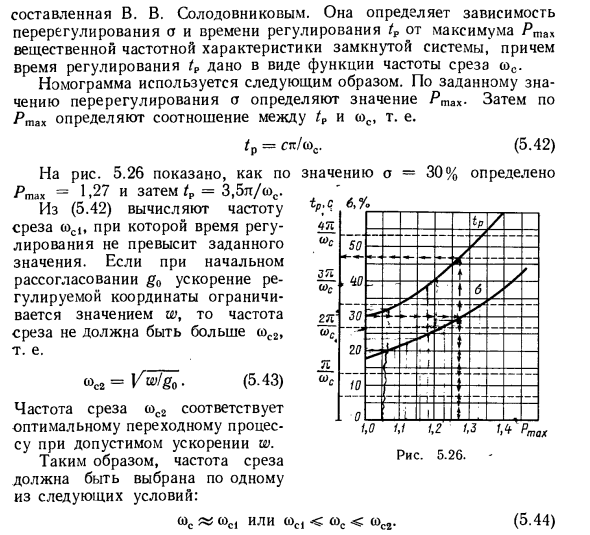
В то же время предполагается, что передаточная функция неизмененной части системы является среднечастотной асимптотой открытой системы LAF и сопряжена с низкочастотной системой, которая определяет динамику: некоторые характеристики системы Является ли стабильность и качественные характеристики переходных характеристик. Построение среднечастотной асимптоты требуемого LAF начинается с выбора частоты среза o> s. В.В, чтобы сделать это. Используйте номограмму, составленную Солодовным новым (рисунок 5.26). Определяется зависимость перерегулирования o и времени управления / P от максимальной частоты Pmax реальных частотных характеристик замкнутой системы, а время управления / P задается как функция частоты отсечки o> s.

Номограмма используется следующим образом: Параметр overshoot определяет значение gsc. Во-вторых, соотношение tP и sos определяется Pmax. / p = pt / sos. (5,42) На рисунке 5.26 значение o = 30% определяет Yatah до 1,27 и tP = 3,5 л / (ос. Из (5.42) рассчитывается частота среза (a1, время управления не превышает установленного значения). Если начальное несоответствие g0 и регулируемое ускорение координат ограничено значением w, частота среза не будет больше, чем со2. «02 = ^^ 0- (5-43)

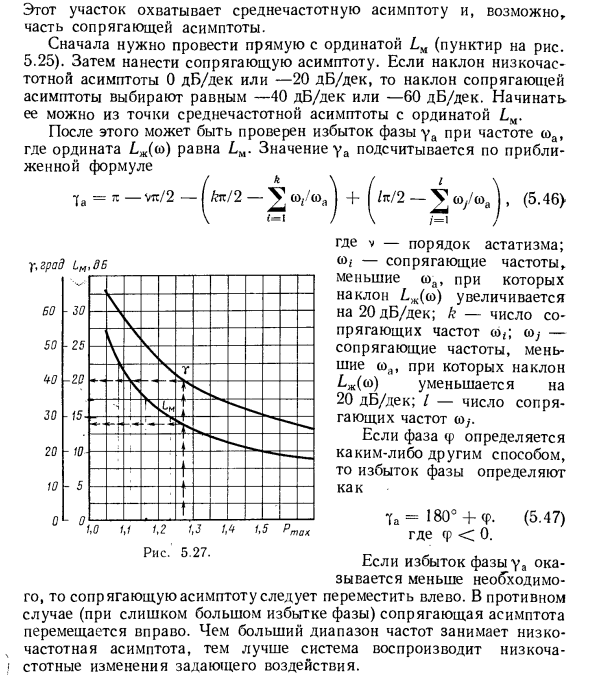
Частота отсечки со2 соответствует оптимальному переходному процессу с эффективным ускорением w. Следовательно, частота среза должна выбираться в соответствии с одним из следующих условий: cac «(oc1 или cac1 s 0> с 271 час 71 (О, т / с 50 /// 40 Вт т / к т ди 30 г 20 … \ < | 1 4- 10 • Я ♦ — ._ J _ Lr —— J-? _ __ 0 1 1 1 —g-1 4- | 1,0 1,1 1,2 1,3 рт.ст. Рисунок 5.26. -Чем больше sos, тем короче время настройки. Однако, если co2 > — ^ M- (5.45) Этот раздел описывает среднечастотную асимптоту и, в некоторых случаях, некоторую сопряженную асимптоту. Сначала вам нужно нарисовать линию с ординатой LM (пунктирная линия на рисунке 5.25). Затем примените асимптоту спаривания.

Если наклон низкочастотной асимптоты равен 0 дБ / дек или –20 дБ / дек, то уклон сопряженной асимптоты выбирается равным –40 дБ / дек или –60 дБ / дек. Людмила Фирмаль

Вы можете начать с асимптоты промежуточной частоты по ординате LM. После этого мы можем проверить, что фаза ya превышена на частоте coa, где ордината £ x (co) равна LM. Значение уа рассчитывается по приближенному выражению b = i-VTC / 2- | w2-2 co, / cod j + ^ / it / 2-2 co / coa j, (5.46) 60 50 b0 30 20 10 -30 -25 Грамм 20 -IS- -10 -5 -0 \ L s \ \ \ To. \ г 1 1 с 1 1 • — 1.2 1.3 Рисунок 5.27. 1,5 р так Где v хаотический порядок. (O — -сопряженная частота меньше, чем coa, где градиент £ x (co) увеличивается на 20 дБ / дек; k — число сопряженных частот co *; co; и градиент £ w (c) 20 дБ / дек. Уменьшается с шагом; / — это число сопряженных частот co /.

Если фазу cp определяют другими методами, избыток фазы определяют следующим образом: fa = 180e (5.47) cp <0. X, степень LM, дБ Если избыточной фазы меньше, чем необходимо, сопряженную асимптоту необходимо переместить влево. В противном случае (если избыток фазы слишком велик), сопряженная асимптота перемещается вправо. Чем шире частотный диапазон низкочастотной асимптоты, тем лучше система воспроизводит низкие частоты. Изменить частоту действий по настройке. Высокочастотная асимптота желаемого LAF мало влияет на характеристики системы.

Поэтому вам следует выбрать максимально корректное устройство коррекции. Это достигается путем объединения высокочастотных асимптот характеристик ж ((ω) и f0 () становится высокочастотной асимптотой L0 ((( Должен иметь тот же уклон, что и d). После выбора высокочастотной асимптоты требуемого LAF и сопряжения ее с асимптотой средней частоты, ордината частоты (y, характеристика жж (ω) равна- / ^, T 7b = — * <7av / 4-2 (0b / (0r, (5,48) Где DSL — относительный наклон асимптоты средней частоты (наклон составляет -20 дБ / декар. Qcv = 1). частота coL-mating, большая частота среза o> s ;: число n-частот ig. е

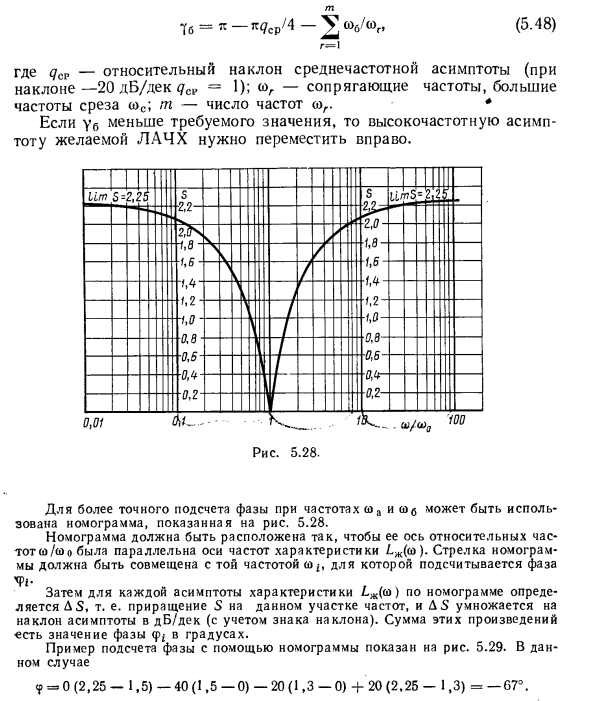
Если Ub меньше требуемого значения, высокочастотная асимптота желаемого LACH должна быть перемещена вправо. Для более точного расчета фазы на частотах а) а и (о <5 можно использовать номограмму, показанную на рис. 5.28. Номограмма должна быть размещена так, чтобы относительная ось частоты (o / coo была параллельна оси частоты характеристики 1zh (o). Стрелка номограммы должна быть выровнена с частотой тона Wj, где рассчитывается фаза Затем для каждой асимптоты характеристики AS определяется из номограммы, то есть приращения S этого частотного участка, и AS умножается на наклон асимптоты на дБ / дека (с учетом знака наклона).

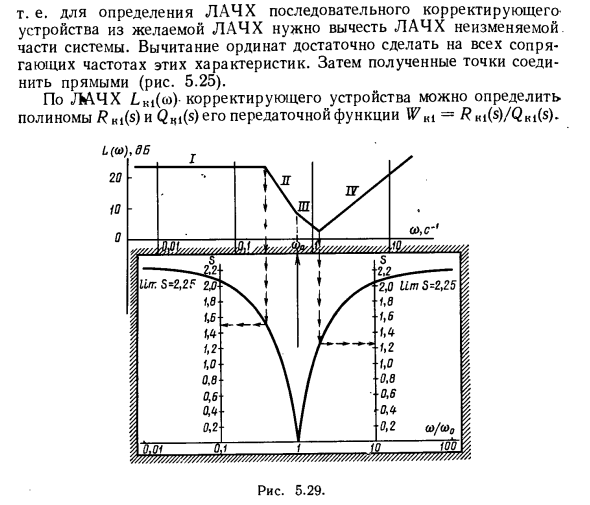
Сумма этих продуктов является фазой в градусах. Пример расчета фазы с использованием номограммы показан на рисунке. 5,29. В этом случае 9 = 0 (2,25-1,5) -40 (1,5-0) -20 (1,3-0) + 20 (2,25-1,3) = -67 ° 1.0 1.1 Выберите корректирующее устройство. Передаточная функция системы с разомкнутым контуром с устройством последовательной коррекции (Рисунок 5.11, a) W = W0WKi9, где W0 = WtWtW9, следующее соотношение справедливо для LAC (Cso) = L0 (o>) + LHi (co). Желаемый LAFL £ w (co) — это LAFL с открытой системой, который необходимо приобрести, установив устройство последовательной коррекции. так Lα (ω) = L0 (ω) + LKi (ω), LKl (ω) LM LM (ω) -L0 (ω), (5.49)

Другими словами, чтобы последовательно определить LAF корректирующего устройства из целевого LAF, необходимо вычесть LAF из неизмененной части системы. Для этих характеристик достаточно вычесть ординату на всех частотах спаривания. Затем соедините полученные точки с прямой линией (рисунок 5.25). Устройство коррекции JK \ 4X Lki (устройства) можно использовать для определения полиномов Rn, (s) и Qhi (s) передаточной функции tt ?? I = Rki (s) / Qki (s). Я спариваю каждую: для частот y, где наклон LAF уменьшается на 20 дБ / дек, соответствует коэффициенту (s / α; + 1) многочлена Rki (s).

Если частота o> »или наклон LACH изменяются на 40 дБ / дек, квадрат указанного коэффициента соответствует этому. Далее, используя уравнение (5.21), передаточные функции Wн2 и \ VH3 для устройств параллельной и прямой параллельной коррекции, соответствующих требуемому устройству последовательной коррекции, должны быть определены соответственно. Если передаточная функция \ VKl является сложной, используйте уравнение (5.23), чтобы определить, какие передаточные функции WKl ‘и WK2’ могут заменить устройство последовательной коррекции, необходимое для двух устройств коррекции (последовательное и параллельное)

Рекомендуется исследовать. На основании полученных результатов и физических характеристик элементов инвариантной части системы вы можете выбрать один из вариантов включения корректирующего устройства. Если нет очевидного и убедительного преимущества одного или двух возможных вариантов, следует рассмотреть все варианты. Учитывая передаточную функцию корректирующего устройства, вы можете выбрать пассивную 4-контактную схему для реализации этой передаточной функции. Простую информацию о пассивных 4-терминальных устройствах можно найти в 5.6. Более подробная информация доступна, например, в 17].

Передаточные функции для полиномов 1-го и 2-го порядка RH (s) и QK (s) легко реализовать. Если степень этих многочленов высока, вы должны использовать два пассивных квадруполя, соединенных последовательно. Основные соображения относительно этой возможности описаны в 5.6. После выбора электрической цепи необходимо рассчитать требуемые значения емкости и сопротивления и убедиться, что вы можете физически запустить эту цепь, используя необходимые параметры передаточной функции. В частности, не используйте пассивные квадруполи с очень малыми передаточными числами (менее 0,1-0,05) или с очень большой емкостью.

Кроме того, не должно быть значительной емкости (или сопротивления) в той же схеме, которая на 2–3 порядка больше и отличается по размеру. Обычно требуемые значения для параметров передаточной функции пассивной 4-портовой сети имеют несколько опций для значений ее элементов. Устройство коррекции также использует активное 4-портовое устройство (см. §5.6). Они имеют большие преимущества, но усложняют систему. Необходимо указать на одну ситуацию. Предположим, что устройство параллельной модификации (рисунок 5.11.6) покрывает часть цепочки со статистикой v-ro порядка. W * = * A (s) / [sv <? 2 (с) J, Где R2 (s) \ Q2 (s) — многочлен от s, равный одному свободному члену.

Корректирующее устройство не меняет порядок статистики в этом разделе цепочки для передаточных функций. kK2RK2 (s) s / \ QK2 (s) \ t (5.50) Где RK2 (s) \ Qh2 (s) — многочлен от s, равный одному свободному члену. W0 (s) = bRAs) / \ s * Q0 (s)], (5.41) Это связано с тем, что передаточное число элемента преобразования усиления и необходимость использования интегрированной связи уже известны. Метод синтеза устройства компенсации, разработанный В.В. Поскольку этот метод используется для систем с минимальным фазовым типом, достаточно учитывать только логарифмические частотные характеристики открытых систем.

Фактически с таким корректирующим устройством передаточная функция рассматриваемого участка схемы = ^ 2 = M «(«) QK2 (S) 2 1 + [Qt (s) QK2 (s) ^ kikKiRt (s) RK.i {s) \ sy То есть статистика сайта остается прежней. Завершающий этап синтеза. При создании целевого LAC предполагалось, что в неизмененной части системы усилителя было необходимое передаточное число. После выбора корректора откройте передаточное число системы, Обычно меняется. И теперь вам, наконец, нужно определить требуемое значение передаточного числа усилителя. Синтез системы завершен. Однако построение желаемого LACH основано на конкретных предположениях.

Кроме того, существует примерная реализация требуемого корректирующего устройства LAF. Поэтому абсолютно необходимо проверить качество синтезированной системы. Для этого строятся миграционные характеристики замкнутой системы и определяются ее качественные показатели. Если система третьего порядка, переходные характеристики удобнее строить операционными методами. «Методология определения корней многочлена описана в начале этого раздела. В системе более высокого порядка следует использовать метод фактических частотных характеристик (трапециевидных или треугольных).

Фактическая частотная характеристика При аппроксимации с отрезком линии необходимо учитывать следующее: начните с начальной точки характеристики, для характеристик с менее сложными формами просто замените 4-5 трапеций (или треугольников) Достаточно, характерный «хвост», то есть последний раздел с ординатой ниже первого 0,1, может быть отброшен. Если системные требования практически не выполняются (во время перерегулирования нормативное время превышает допустимое отклонение), вы должны найти и устранить причину сбоя в решении.

В дополнение к ошибке вычисления, неточная реализация требуемой передаточной функции корректирующего устройства с выбранным электрическим 4-контактным разъемом, неточное приближение требуемого корректирующего устройства LAC с этой передаточной функцией, а также частота управления ωa и o> T Недостаточная фаза окончена). Могут быть существенные различия между фактической частотной характеристикой синтезированной системы и типичной характеристикой номограммы (рисунки 5.26 и 5.27), на которой основаны вычисления. В последнем случае необходимо повторить расчет и установить значения o и / P меньше требуемого.

Пример 5.3 Настраиваемые объекты и исполнительные элементы системы слежения за устройством описываются передаточными функциями W0 (s) = k / \ s (0,05 с — + — 1) (0,01 с + 1) 1- Должен быть выбран последовательный корректор, который обеспечивает следующий индекс качества с k = 200 с-1 и v = I. o «30% и tp <0,5 с. Допустимое ускорение регулируемых координат w = 50 рад / с2, начальное несоответствие go = 0,1 рад. Перед началом расчета обратите внимание, что система с k-200 и без корректирующего устройства нестабильна. На самом деле, в этом случае характеристическое уравнение 0,0005 с3 + 0,06 с * + с + 200 = 0 И идентификатор Гурвица a ^ -o ^ s = 0,06 -0,1 = -0,04 <0.

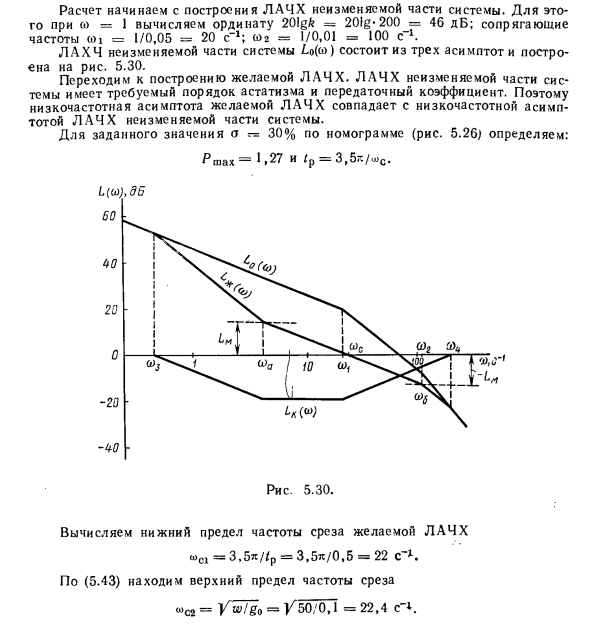
Начните вычисление, построив LACH неизмененной части системы. Для этого рассчитайте ординату с помощью (o = 1 20 logfc = 20ig * 200_ = 46 дБ; 1 = 1 / 0,05 = 20 с «1; co2 = 1 / 0,01 = 100 с K fit Комбинированная частота Инвариантная часть системы LAHCH состоит из трех асимптот и одного компонента. Фиговая хна. 5,30. Продолжайте строить желаемый LACH. LACH неизмененной части системы имеет необходимый беспорядок и передаточное число. Следовательно, низкочастотная асимптота желаемого LAF совпадает с низкочастотной асимптотой LAF в неизмененной части системы.

Для определенного значения a 30% от номограммы (рисунок 5.26) определите: Pmax = 1,27 и /p = 3,5 г. / O> с. L (0i), дБ Рисунок 5.30. Рассчитать нижний предел целевой частоты среза LACH bc1 = 3,5 * / fp = 3,5 * / 0,5 = 22 с’1. Найти верхний предел частоты среза по (5.43) «C2 = V ^ Tgo = / bOTOL = 22,4 с-1. По выбору пользователя). , = 22 с 1 И, через эту точку, нарисуйте среднечастотную асимптоту желаемого LACH с ранее рекомендованным градиентом 20 дБ / дек (рис. 5.30). Кроме того, в соответствии с кривой для Pmax = 1,27 (рисунок 5.27) мы определяем, что для координаты LM (± o = в пределах 14 дБ (o)) требуется перепад фазы y = 40 °. Нарисуйте линию по ординате -M4 дБ и постройте асимптоту тестового перехода с уклоном 40 дБ / дек от пересечения с асимптотой средней частоты желаемого LAC.

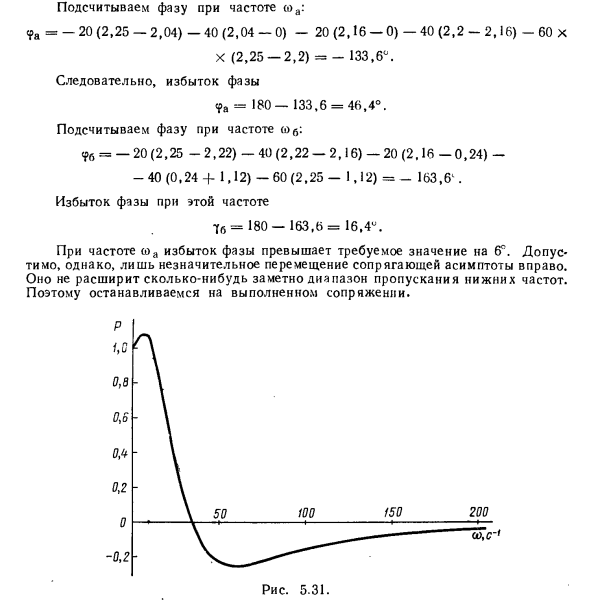
Целевой высокочастотной асимптотой LAF является высокочастотная асимптота LAF неизмененной части системы. Связь требуемой асимптоты промежуточной частоты LAF и высокочастотной асимптоты начинается с частоты 2. Теперь нам нужно проверить превышение фазы на контрольной частоте (используя a и номограмму для расчета фазы в соответствии с асимптотическим LAF, показанным на рисунке 5.28.Рассчитать фазу на частоте коа. ? а = -20 (2,25-2,04) -40 (2,04-0) -20 (2,16-0) -40 (2,2-2,16) -60 х Х (2,25-2,2) = -133,6 ° В результате превышение фазы 9а = 180-133,6 = 46,4 °. Рассчитать фазу на частоте d> 6. % = -20 (2,25-2,22) -40 (2,22-2,16) -20 (2,16-0,24) — -40 (0,24-L 1,12) -60 (2,25-1,12) = _ 163,6 ‘.

Избыточная фаза на этой частоте А = 180-163,6 = 16,4. На частотах o> a превышение фазы превышает требуемое значение на 6 e. Однако допускается только небольшое движение вправо от сопряженной асимптоты. Заметный низкий диапазон не расширяется. Поэтому выполненное сопряжение описано. Рисунок 5.31. Избыток фазы при с & g значительно ниже приемлемого диапазона. Чтобы увеличить его, нужно сдвинуть высокочастотную асимптоту желаемого LACH вправо. Это усложняет устройство коррекции. Давайте проверим качество системы, используя целевой LAC. Желаемый фактор определяется. (Co) составляет передаточную функцию открытой системы коррекции. w ^ _ + 0 = 200 (0,24 с + 1) S (S / U) 3 + I) (s / 2 =, 100 с «1; a> 4 = 174 с» 1.

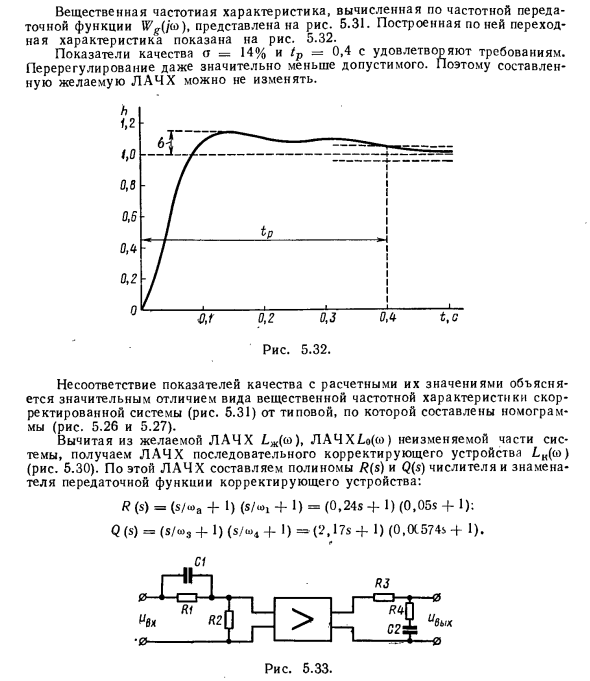
Передаточная функция с замкнутым контуром IVK [s) = W (s) / | l + U? (S) | = (0,24 с + 1) / (6,25 • I0 «7s4 + 1,72 • 10» «s3 + 4-0.011s2 4-0.245s + I). На рисунке 5 показана фактическая частотная характеристика, рассчитанная по передаточной функции частоты Wg (ja) t. 5,31. Результирующий переходный ответ показан на рисунке. 5,32. Качественные показатели а = 14% и / р = 0,4 с соответствуют требованиям. Overshoot намного ниже допустимого. Следовательно, скомпилированный целевой LACH не может быть изменен.

Рисунок 5.32. Несоответствие между показателем качества и его рассчитанным значением объясняется существенным различием между типом частотной характеристики материала настроенной системы (рисунок 5.31) и стандартной системы с составленной номограммой (рисунки 5.26 и 5.27). Целевой LACH /.* (<■>) »LACHXLo ((o) Вычтите из неизмененной части системы, чтобы получить LACH устройства последовательной коррекции LK (w) (рисунок 5.30). Используйте этот LACH Числитель и знаменатель передаточной функции устройства коррекции полинома R (s) и Q (s): R (s) = (s / a> af-1) (S / u> x 4-1) = (0,24 с + 1) (0,05 с + I): Q (s) = (с / «S + 1 ) (S / u «4 + I) = (2,17sf 1) (0, (X574s + 1). Рисунок 5.33.

Желаемая передаточная функция корректирующего устройства может быть реализована путем дифференцирования и интеграции 4-контактного устройства с отдельным усилителем (рисунок 5.33). Дифференциальная квадрупольная передаточная функция WKl (s) = feKα (Γ | α + 1) / (Γ * + 1). Где 7j = 0,05 = /? A; T2 = 0,00574 = H2G, / (/?, + H2). Значение сопротивления /? G должен быть выбран при расчете усилителя. Затем вы можете определить необходимые значения для Ri и Ci и рассчитать значение kKl. … Построение постоянной части системы LACH. Асимптотический LAFC L0 (co) должен быть построен из передаточной функции 0 0 (s), определенной в (5.41).

Во-первых, каждый многочлен R0 (s) и Q0 (s) передаточной функции W0 (s) должен быть учтен как Tts 4-1 и 7y s2 4-2 Tjb 4-1. <1. Это разложение о. Его удобно выполнять итерационным методом, предложенным М. Крыжановским. Оператор метода и пример его применения показаны в (8). Предположим, у вас есть кубический полином G (s) = a ^ 4. axs2 -f 1 = a0 (s3 c, s2 4-c ^ s + c3), Где cx = a, / a0; c2-a2 / a0 и c9- / Oq. Вычислить a, = c3 / s2. Eh-stj (s, -a,); A2 = CE / (C2-% = H-II2) ‘” * i = c91 (c2-b2) \ и т. д. Значение a, когда процесс сходится, то есть i увеличивается. И есть определенные пределы а и р соответственно. тогда G (s) = (s / i + 1) (acifjs2 4-? Ооs4-1). / Процесс расчета ир. Это может быть по-другому.

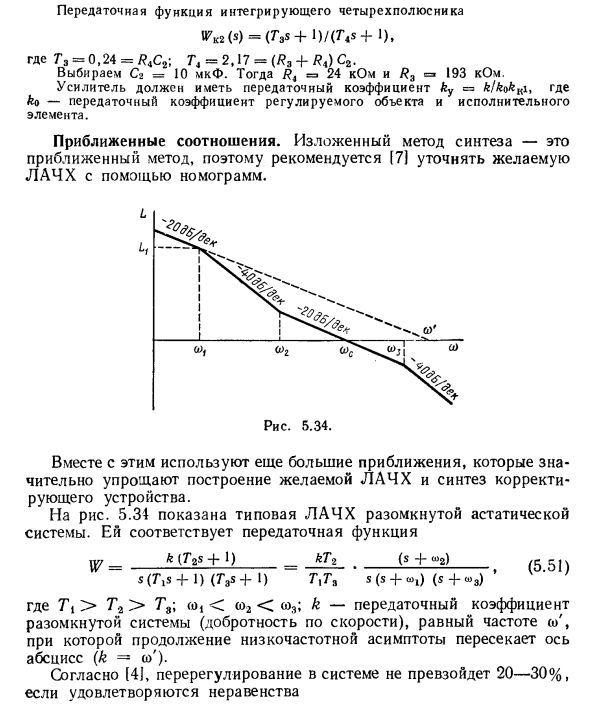
Тогда вам нужно сделать такой расчет. A1 = c2 / c1 — c3 / s21; «2 = ^ / (^ 1-» i> — ^ i) 2: а9 = с2 / (с1-а2) -с9 / (Cr-H2) 2 и т. д. После определения предела a, к которому идет значение aj, получаем G (s) = (a0s / r 4-1) (rs * 4-ars + 1). R задницу а-а-а здесь. Предположим, у вас есть полином 4-го порядка G (s) = a0s4 4-axs3 4-a2s * 4-OgS 4-1 = a0 (s1 -f- cxs * -f-с4-CyS 4-c4), Где c = ajao: c2 = a2 / 4>; c3 = a3 / a0 и c4 = I / a0. Рассчитать a = c4 / c3; = ax (c, -ai); f = s. (5.53) Таким образом, заданное значение k может определить частоту o /, а затем создать прямую линию с низкочастотной асимптотой искомого LAC. С другой стороны, целевую частоту среза LACH можно определить из (5.53), используя настройку времени / P. Частоты ). Вы можете быть абсолютно уверены Игнорировать двоичные и троичные выражения для T9 <. Здесь coC0 — это частота, на которой характеристика L0 (co) пересекает горизонтальную ось (частота среза этой характеристики).

Используйте рекомендации, сделанные в II, с. 212), можно более точно определить влияние малых постоянных времени и допуск игнорировать их. На рисунке 5.25 показана системная характеристика L0 ((o), приблизительная форма астеризма первого порядка). Постройте желаемый LACH. Называется асимптотической LACH £ (со) открытой системой с желаемыми (обязательными) статическими и динамическими свойствами. Целевой LAF (см. Рисунок 5.25) состоит из трех основных асимптот: низкая частота, средняя частота и высокая частота. Кроме того, могут быть асимптоты, соединяющие основные.

Целевой LACH строится на основе системных требований. Ранее было известно, что низкочастотная асимптота кривой LAC с разомкнутым контуром определяет статические характеристики. Низкая частота, если передаточная функция открытой системы (5.41) имеет коэффициент передачи k и статистический порядок V, которые отвечают требованиям Требуемая асимптотика LACH £ ((o) является низкочастотной асимптотой немодифицированной части системы LACH L L0 ((o). На рисунке 5.25 показан такой случай). Сопряженность низкочастотной системы с средней частотой асимптоты частоты LAC системы с разомкнутым контуром определяет динамику. Некоторые свойства системы являются характеристиками стабильности и качества переходных характеристик. Построение требуемой частоты LAC из низкочастотной асимптоты начинается с выбора частоты среза sos. Для этого используйте номограмму (рисунок 5.26).

Новое составлено В. В. Солодовным. Определите зависимость перерегулирования o и времени регулировки tP от максимального значения Pmax частотной характеристики материала замкнутой системы, где время регулировки tP дано как функция частоты среза ss. Номограмма используется следующим образом: Заданное значение превышения a используется для определения значения Pmax, а отношение tP к toc определяется как Pmax. / p = G1t / o> s. (5,42) На рисунке 5.26 показано, как Yashav = 1,27 определяется со значением o = 30%, а затем /p = 3,5 л / о) с. Из (5.42) частота отсечки a> c1 рассчитывается таким образом, чтобы время управления не превышало установленного значения. Для первого расхождения g0, если регулируемое ускорение координат ограничено значением w, частота среза не должна превышать со2. «02 = ^^ 0. (5-43)

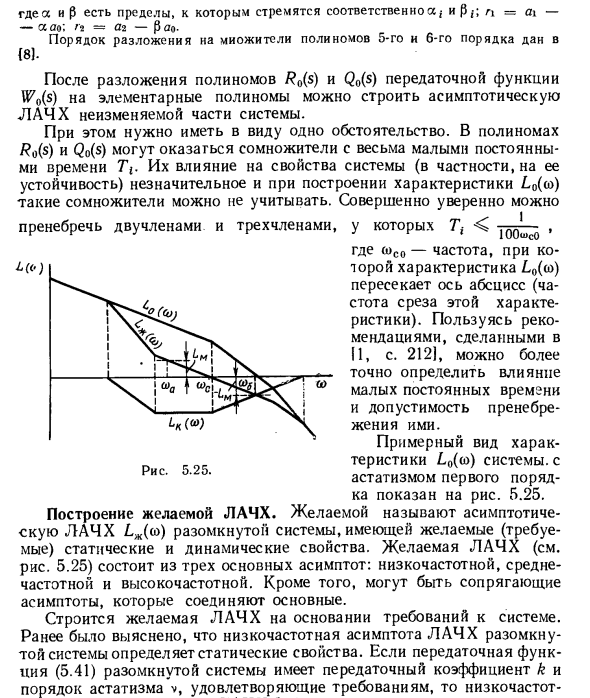
Частота отсечки a> c2 соответствует оптимальному переходному процессу с допустимым ускорением w. Следовательно, частота среза должна выбираться в соответствии с одним из следующих условий: (Σα ((σ1 или (1> c1 << σ > — ^ M- (5.45) После разложения многочленов R0 (s) и Q0 (s) передаточной функции W0 (s) на основные многочлены можно построить асимптотический LAF немодифицированной части системы. В этом случае вам необходимо знать одну ситуацию. Полиномы ρ0 (s) и Q0 (s) имеют очень малую постоянную времени 7V. Влияние на характеристики системы (особенно ее устойчивость) незначительно, и такие факторы являются характеристикой L0 ((o), в которой вы можете быть абсолютно уверены Игнорировать биномы и троицы T9 < Xj Lh \ Chg Ch LK (o>) Рисунок 5.25. «100u> c0 Где a> co — частота, co-1 (o), характеристика L0 (до)

Пересекает горизонтальную ось (частота среза для этой характеристики). Используйте рекомендации, сделанные в II, с. 212], можно более точно определить влияние малых постоянных времени и допуск игнорировать их. На рисунке 5.25 показана системная характеристика L0 ((o), приблизительная форма астеризма первого порядка). Постройте желаемый LACH. Открытая система асимптотики LACH (L Ju) с желаемыми (обязательными) статическими и динамическими свойствами. Целевой LAF (см. Рисунок 5.25) состоит из трех основных асимптот: низкая частота, средняя частота и высокая частота. Кроме того, могут быть асимптоты, соединяющие основные.

Метод аппроксимации кругом	Построение областей устойчивости в плоскости параметров системы
Количественные критерии оценки устойчивости по нормам и по следу матрицы В	Устойчивость систем с запаздыванием и систем с иррациональными звеньями