Оглавление:





Синтез двухполюсников, основанный на последовательном выделении из функции входного сопротивления
Двухполюсный синтез, основанный на последовательном отделении простейших компонентов от функции входного сопротивления. Задача выглядит так:
- Известно уравнение для входного сопротивления Z (p) = для двухполюсного устройства, которое
удовлетворяет требованиям по физической выполнимости. Людмила Фирмаль
Вам нужно сформировать схему и последовательно извлечь самые простые компоненты из функции входного сопротивления, чтобы найти значения их компонентов. Рассмотрим один из возможных способов решения проблемы. 1.
Сначала выберите компонент, пропорциональный первой степени p из композиции Z (p). Происходит, когда порядок A (p) на один выше, чем порядок B (p). Идентифицированный компонент имеет вид ± р.
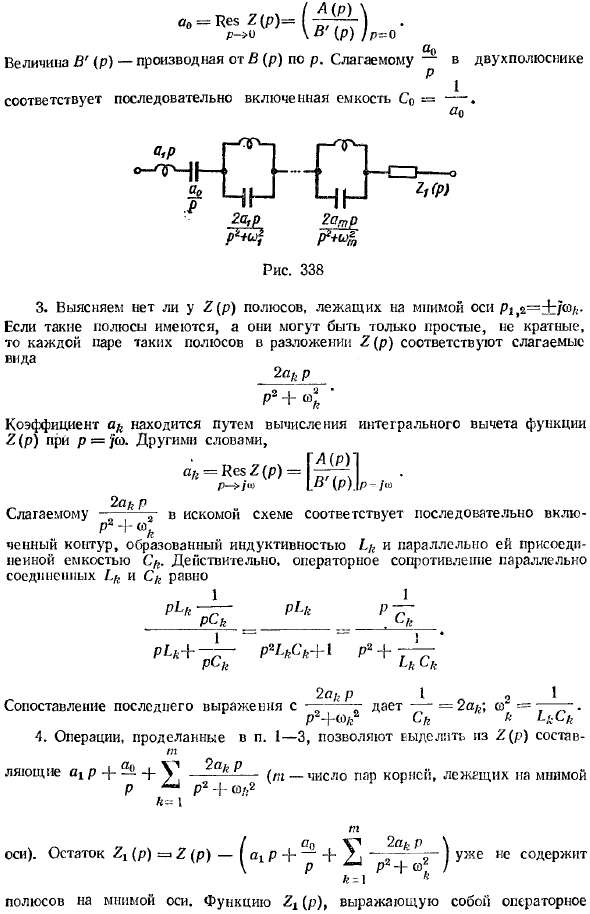
- Где aY — индуктивность, в которой начинается двухполюсник (Рисунок 338). A (p) 2. Проверьте, имеет ли Z (p) = полюс с p => 0 (корень уравнения B (p) = zO называется полюсом). Если Z (p) имеет полюс при p = »0, форму-член следует отличать от Co Z (p).
Коэффициент равен p = 0, то есть целочисленный остаток функции Z (p) для ao. — Если 2-контактная клемма РI соответствует емкости Co = — • ao 3, включенной последовательно.
Величина B ‘(p) является производной от B (p) по p. Людмила Фирмаль
Проверьте, имеет ли Z (p) полюс на мнимой оси Pi. 2 = + / ® / .- просто, кратно только ns, тогда каждая пара таких полюсов расширения. Z (p) соответствует члену вида 2 ^ P P3 + <•. Коэффициент ak получается путем вычисления интегрального остатка функции Z (p) при p = po. То есть, ах = Res Z (p) = («TTs] P-> jw I» (P) .1l- / «> 2 (1 / gp).
Целевой элемент схемы формируется параллельно с индуктивностью Lk. В соответствии со схемой последовательного соединения, сопротивление оператора Lft и Ck, соединенных параллельно, фактически равно 1 1 P’-fr -r-pt-k Pg _ PrgA, cfe pLk + ~ P2I * Ck + 1 P2 + ~ P ^ k l’k в последнем выражении c — — = 2am co2 ==, P 4- —9 I kc
Уже содержит pP4® / Ft = lk на мнимой оси полюса и согласился вызвать функцию Zx (p) 5. Дальнейшее формирование двухполюсной сети — это функция минимального реактивного сопротивления (p)
Эта операция может привести к следующим случаям: а) Zj (p) является действительным и положительным В двухконтактной схеме это реализуется с помощью ряда активных резисторов 339 a.b) Zj (p) является частью формы, а At (p) является постоянным nc-зависимым членом 0i (P)
Не включается, т. Е. (P) таково, что p-0 равно нулю Zj (p) P. В этом случае Zx (p) является суммой долей вида p, т.е. 7 VP ^ 1 (P) = Aj может быть разложен • «p4- / ny ak p-type parts» • 2-контактная схема соответствует цепи последовательного соединения, образованной параллельно индуктивностью Ln и активным сопротивлением Rn ,
Обратитесь к рисунку 339, б. Это Rnt равно параллельному соединению Ln, по сравнению с -k ~. Сравнение для схемы cif {^ Rrl и ./dl = 10, реализующей ZA (p), последовательное активное сопротивление, равное C. Zj (p) = (p) не зависит от ° i (P) В этом случае Zx (p) можно выразить следующим образом: (P) = J] nl_A «b.
Каждая часть схемы Zt (p) представляет собой емкость C / И параллельное соединение сопротивления R / t (рис. 339, в). Фактически, связанное с оператором сопротивление Ck и Rk, соединенных параллельно, составляет ~ P + R ^ k „bk II Сравнение с: -и БД. P + rfft Ck * RkCk 6.
В заключение, если функция минимального (P) реактивного сопротивления Zx (p) = -is (p) равна нулю, то есть (P) корень уравнения A1 (p) на мнимой оси ^ ^ 0 лежит p-zti ^ k, чтобы PRI P-Zi (p) формируется путем построения обратной дроби: y ~ L = 1 2i (p) Л (p) ‘, разлагаем ее в том же порядке Описано в пунктах 1-4 выше.
Конечно, разложение а) с? GT4! } 1 6> 4Lb4xj “Tt Рисунок 339 Рисунок 340 уже физически реализован в виде последовательно соединенных резисторов a, p. И Zj (p), как в Z (pi и P2). P2 -Ilt 2 <Tp, в виде параллельного соединения ветвей проводимости p, -, и pp * -No ‘Y2 (p) L (p) p: t [p2-i-2p
Пример 150. Функция Z (P) = — == • -I (P) p * + p2- ‘, должно быть реализовано решение p I 1. По вышеуказанному методу: 1. Порядок A (p) — B (p) Поскольку они равны, == 0, то есть двухполюсная сеть не имеет индуктивности последовательного соединения 2. Z (p) не имеет полюсов при p = 0.
Поэтому требуемая биполярная конфигурация соединена последовательно 3. Z (p) имеет два полюса на мнимой оси. Фактически B (P) = (P * 4 “0 (P + O-, следовательно, p ( 2 = ± / .. P = 4- / Остаток Z (p) действителен, потому что оба остатка от p = -j действительны : A (p) = P34 ~ P24 ~ 2p = -1.4-2 / = 1 «x = Res Z (p) p = ~ -i B ‘(P) Zp24-2p4-1- 3 4-2 / 4- 1 2 * p = / p ^ i
Определите значения f4 и C ^ Cr4, соединенных параллельно от Z (p) до реактивного сопротивления P2-L Z, (p); PP * + 1 и минимальной функции z (P ) P3 * pa + 2p-pr 1 p3-bpChr + 1 p2 + 1 pm ‘5. Структура Zx (p) соответствует тому, что описано в § 56, поэтому Z, (p) Работает в форме параллельных соединений L2 => 1 и /? 3 = 1.
Показывает схему нужного двухполюсника. График: графен формулы Мейсона — это набор узлов и ветвей, которые их соединяют. Существует два типа графиков: ненаправленные и направленные. Узлы и ветви неориентированного графа соответствуют узлам и ветвям рассматриваемой электрической цепи.
Геометрическое изображение или скелетная диаграмма, график направления (график сигнала или (Также называемые диаграммами потоков сигналов), узлами обычно являются ток и / или напряжение, и каждая ветвь характеризуется величиной передачи (отношение выходного значения этой ветви к входному значению этой ветви).
На ветвях появляются стрелки, указывающие направление передачи. Основная формула теории графов — формула Мейсона. Предположим, что это относится к ненаправленному графику: / V / np, где / — ток, протекающий вдоль выбранной ветви графика, где определяется входная или взаимная проводимость, а Vn — источник
Напряжение е. d.s или ток источника тока, подключенного к узлам t и l. Cr — произведение проводимости ветви пути между узлами m и n, которая проходит через выбранную ветвь. При прохождении по этому пути Cr будет иметь знак плюс, если выбранная ветвь обходит эту ветвь, условно выбранную в соответствии с положительным направлением.
Ar является определителем схемы, полученным из исходной схемы путем замыкания всех ветвей пути Cr. Общее количество членов равно числу возможных путей между узлами m и l на графике (количество путей не включает в себя путь от l до l через схему питания).
А является определяющим фактором всей схемы. Несколько методов (разложение по узлам, разложение по ветвям) было разработано для облегчения вычисления A и Ar, но здесь считается недостаток места (см. L. 9).
Смотрите также:

