Оглавление:









Симметрия по отношению к перестановкам
- Перестановочная симметрия Рассматривая систему, состоящую только из двух частиц, Можно утверждать, что координатная волна работает на 100 Стационарное состояние <p (1 * 1, G2) должно быть симметричным, Либо антисимметричный. В общем, система из Количество свободных частиц в решении уравнения Шредингера Определить волновую функцию).
- Симметричный или асимметричный В перестановке любой пары частиц, как в Полная волновая функция (включая спиновый коэффициент). Физическая идентичность частиц здесь Гамильтониан системы неизменен Если частицы, и, следовательно, какая-то функция является решением Уравнение Шредингера, решение является функцией Излучение от источника через различные перестановки Переменный.
Это потому, что перестановка только координат Две частицы еще не совместимы с физическим перемещением. Людмила Фирмаль
Сначала сделаем несколько замечаний о перестановке Вовсе нет. В системе с N частицами возможен только N1 раз Личная перестановка. Представь себе все частицы Перенумерация может представлять каждую перестановку Определенная последовательность чисел 1, 2, 3, … Вы можете получить любую последовательность от природы Последовательность 1, 2, 3, … последовательная замена Пара ми частиц.
Перестановки называются четными или нечетными В зависимости от того, является ли это нечетным или четным Количество парных перестановок. P указывает на оператора Введем перестановку из N частиц и значение Sp, +1, равное ес Является ли P четной перестановкой, и -1, если перестановка нечетная Не. Если <р является симметричной функцией для всех частиц, Пип = (р, §63C I M M E T R I O O T N O S N Y Y K P E R E S T A N O V K A M 291
И если функция асимметрична по всем частицам, Пипс = 8 пипсов Из любой функции (p (Tx, T2, …, Gd) Для создания симметричной функции используются симметричные операции Nation. Вы можете написать: Итого выполняется максимально Newcomer. Формирование антисимметричной функции (это операция (Иногда называют радио) Сано в форме Проблема поведения волновой функции <p Система идентичных частиц с перестановками 1).
Дело в том, что в системе гамильтонианы все симметричны Частица математически означает, что она коммутативна с Все операторы перестановки P. Тем не менее, эти операторы Не может быть личным, потому что они взаимно коммутативны Они находятся по диагонали одновременно. Это корова Новая функция (p не может быть выбран, Симметричный или антисимметричный Все индивидуальные парные перестановки 2).
Возникает проблема определения возможных типов симметрии Ri функции N переменных (p (Gx, Gx, …, gdg) Функции некоторых таких функций относительно замены) Переменный. Симметрия должна быть такой, чтобы она не могла Выше, то есть дополнительные симметричные операции Чередование или чередование применительно к этим функциям Объедините их линейно или Так же, как ноль.
1) С математической точки зрения проблема состоит в том, чтобы найти Заменяемое представление замещающей группы. Детальные товары См. Книгу теоретической теории групп перестановок: Г. Weil. Теория групп И квантовая механика. -М. : Наука, 1985; М. Хамелмеш. Теория групп и ее Приложение к физическим проблемам. -М. : IL, 1966; И.Г. Каплан. Сим Мультиэлектронная система показателей. -М. : Наука, 1969.
2) Только один оператор для двухчастичных систем. В то же время можно уменьшить до диагонали С гамильтонианом. Я уже знаю две операции, которые приводят к функциональности Максимальная симметрия: симметризация всех переменных Переключает все переменные поочередно.
Эти операции Это сводится к следующему: Разбейте множество всех N переменных ri, G2. , , , Б-г (Или то же самое, индекс 1, 2, 3, …, N) Элементы серии (переменные), включая iVi, iV2, … Ni + + N2 + … = N. Такие перегородки можно визуализировать Схема (так называемая молодая схема), каждая Насыщенный Ni, L / 2, … представлен несколькими рядами клеток ( На рисунке 2 показана схема разбиения 6 + 4 + 4 + 3 + 3 + 1 + 1 Для N = 22, 7 + 5 + 5 + 3 + 1 + 1), следует за каждым квадратом.
Введите одно из чисел 1, 2, 3, … Порядок сокращения (как сделано на рисунке 21), затем схема Не только непрерывное горизонтальное направление Не только строки, но и вертикальные столбцы. Выполнить любую функцию симметризации Что касается переменных, которые составляют каждый? (Я * я, G2, …, GDG) С линии.
После этой операции _ я я __ я ——— ———— только Различные включенные переменные _ny line; чередование ЖЖ пара переменных в Очевидно, в одной строке Рисунок 2 1 по сути ноль. Выберите из каждой строки Одна переменная, не теряя общности Растопить их в первой ячейке ряда (после симметрии) Порядок массива переменных в каждой ячейке Линия не важна), мы используем их поочередно С поясом.
Уберите первый столбец и сделайте все Повторите переменные, выбранные из каждого Линии сокращены таким образом. Эти изменения сейчас Нью-Йорк может снова считаться в первой ячейке Линия неттинга. Продолжайте этот процесс, и мы придем в фанк.
Сначала симметризируется каждой структурной переменной ки и поочередно в каждом ряду (Конечно, вообще говоря, после изменения функций, Каждая строковая переменная больше не является симметричной; Симметрия длится только в отношении изменений В ячейке первого ряда Другая линия).
- Распределение N переменных по порядку Схема Кэм Янга (распределение клеток в каждом ряду §63C I M M E T R I O O T N O S N Y Y K P E R E S T A N O V K A M 293 (Слегка) получить набор функций таким образом Конвертировать с любой перестановкой переменных 1) через друг друга. Однако следует подчеркнуть, что не все Эти функции линейно независимы.
Количество независимых функций Как правило, меньше, чем количество возможных распределений Переменная в соответствии со строкой схемы. Поэтому каждая схема Юнга имеет определенную схему Второй тип функциональной симметрии относительно перестановок.
Я не могу остановиться здесь 2) для более подробной информации по этому вопросу. Людмила Фирмаль
Настройте все схемы Юнга (для данного N) Найдите все возможные типы симметрии. Кипятить Номер N всеми возможными способами В меньшие сроки и возможные разделы Само число N также включено (например, если N = 4 Перегородки: 4, 3 + 1, 2 + 2, 2 + 1 + 1, 1 + 1 + 1 + 1). Может быть введен в каждый энергетический уровень системы.
Поддержка нескольких схем Юнга для определения Устанавливает симметрию соответствующего решения уравнения Шредингера, в этом случае каждое значение энергии Эм, вообще говоря, несколько разных функций Установите, чтобы конвертировать друг друга.
Существование этого «Перестановочное вырождение» уже упоминалось Некоммутируемость оператора P соответственно Мутация с гамильтонианом (ср. § 10, стр. 48). Подчеркните OD Однако это не подразумевает дополнительного присутствия Физическая модификация энергетических уровней.
Все эти различия Функция координат, умноженная на спин Особенности включены в одну конкретную комбинацию (пол) Волновая функция-удовлетворенность (зависит Спин частиц) Симметричное состояние или антисимметричное состояние STI Среди различных типов симметрии всегда N) 2 задано и соответствует только одной функции Вы.
Один из них соответствует симметричной функции Переменная, а другая — асимметричная (первый случай Можно выполнить симметризацию и замену в 1). Первичные переменные сначала с переменными в каждом столбце Он симметричен переменным ts и line. Но это не Функции, полученные с помощью обоих методов Линейная комбинация друг друга.
2) Независимые функции, которые преобразуются друг в друга Основа неприводимого представления группы замещения. Эти цифры Функция — это измерение выражения. Для частиц со спином 1/2 определено в вопросе 1 этого раздела. Схема Юнга состоит только из одного ряда N клеток, Со второго -1 столбца).
Посмотрите на функцию спиновой волны x (cri, 0 2, …, sgdg). Типы симметрии для перестановок частиц Роль ne определяется по той же схеме Юнга Проекция воспроизводится путем проецирования спина частиц. Вопрос Какая схема соответствует спиновой функции Определение заданной схемы координатной функции.
временно Во-первых, частицы полностью вращаются. Тогда завершите Волновая функция g / j должна быть симметричной во всех частях цы. По этой причине симметрия спиновых и координатных функций Должна быть определена по той же схеме Юнга, завершена Волновая функция φ выражается в виде определенного билина Все остальные комбинации с ними, никогда не останавливайся Теперь о проблеме составления этой комбинации.
Здесь дайте частице половинное целое вращение. тогда Общая волновая функция Все частицы. Об этой схеме Юнга, Координаты и функции вращения должны быть двойными: Добирайтесь друг до друга, заменяя строки столбцами и наоборот (Например, две схемы, показанные на фиг. 21). Мы подробно обсудим важный случай частиц со спином. Ном 1/2 (например, электронный).
Каждый раз, когда вращение меняется Есть только два значения с числовыми значениями <7 1, (7 2, …, ± 1/2. Поскольку функция асимметрична относительно любых двух Переменная исчезнет, если эти переменные совпадают Понятно, что значение функции% можно изменить Только переменные пары.
Alternani осел уже 3 переменные, по крайней мере 2 из которых Имеют одинаковое значение, так что вы можете видеть, что они абсолютно одинаковы Ноль. Поэтому в электронной системе схема Юнга Функция вращения может содержать только один столбец Ну или две клетки (т.е. 1 строка или 2 строки); Та же диаграмма координатных функций Линия.
Количество возможных типов перестановочной симметрии Таким образом, система из N электронов Разделите N на сумму 1 и 2. Четный N Это число равно N / 2 + 1 (0, 1, …, 7V / 2 2 раздела) Нечетные (N + 1) / 2 (0, 1, …, (N-1) / 2 раздела 2). Таким образом, на рисунке 22 возможна схема Юнга (Координаты и вращение), когда N = 4
Каждый из этих типов симметрии (т.е. Схемы Юнга) соответствуют определенным полам Spin S электронной системы. рассматривать §63C I M M E T R R I O T T N O SH E N I Y K K P E R E S T A N O V K A M 295 Спин-функция, то есть спин-функция в виде спинора Ранг iV-ro и его индекс (соответствующий каждому Будет доминировать сзади отдельных частиц) В клетке Схема Юнга.
Думать о спине Новая схема Юнга, состоящая из 2 ряда с клеем N ± и N2 В настоящее время (iVi + N 2 = N, N 1 ^ N 2). в Есть два в первых N столбцах 5 = 2 5 = 1 5 = 0 для ячейки и соответствующей пары Индекс блесны анти 2 2 Симметричный. По индексу Наконец-то n = N ± -N2 В первом ряду ячеек счетчик должен быть симметричным.
но Как мы знаем, такие спиннеры iV-ro ранга снижают симметрию Спин-спиннер Nth для полного Вернемся к схеме спин-юнга, равной S = n / 2 Функция ординаты, схема с п Ками с одной клеткой Спин при полном вращении S = n / 2. Четный N, полный оборот Может иметь целочисленное значение от 0 до N / 2 и нечетное число N-половинное целое значение от 1/2 до N / 2, если требуется Быть.
Подчеркните этот уникальный ответ Юнга Схема полного вращения Спин 1/2, для систем только с двумя частицами мы убедились Это уже объяснялось в предыдущем абзаце. Для системы с N частицами Для спина s функция спиновой волны Редукция N симметричных спиноров ранга 25, то есть Уровень 2 Ns.
Это спинор Используя конкретную схему Янга из N клеток, Такой симметризованный спинор-зависимый компонент Обычно образует несколько наборов линейных комбинаций, Соответствующие различным значениям общего спина s S. Stem Подобно частицам со спином 1/2, схема Юнга является спиновой Новая функция не может содержать более 2 столбцов Моя клетка, поэтому для частиц с любым спином 5 длины.
Столбец не должен превышать 25 + 1 клеток. Если число N частиц в системе является целым числом, кратным 25 + 1 Среди возможных схем Юнга прямоугольные схемы ма, каждый столбец содержит 25 + 1 клеток. Такая схема Me соответствует одному конкретному значению общего вращения, S = 0. В общем, любые два (спин) йона Эскизы, которые можно объединить в прямоугольники Такое же значение для 2 s + l high, S 1) соответствует.
Этот вывод Есть просто два случая Полицейский может сделать суммарный момент равным нулю, Когда добавленный момент имеет тот же размер. Я уже упоминал в конце этого раздела Состояние системы с предыдущего (см. Примечание на стр. 8 6) Некоторые идентичные частицы не могут претендовать на волну Функция установившегося режима с наименьшей энергией У нее нет узлов.
Это проясняет это утверждение, Найдите его происхождение. Не волновая функция (если говорить о координатных функциях) Есть узлы, должны быть симметричными вообще Частица, если она не симметрична Перестановка любой пары частиц 1 и 2 Когда i * i = Г2, это ноль.
Однако, если система состоит из 3 или более Электрон, то идеально симметричная координатная волна Функции не разрешены (схема координат Юнга Функция не может содержать строки с более чем двумя ячейками). Следовательно, это решение уравнения Шредингера, но соответствующее Это наименьшее собственное значение и не имеет узла.
Однако поймать (по вариационной теореме), это Решение не может быть физически приемлемым. Потом опять Минимальное состояние системы — не менее Шея и волна от собственных значений уравнения Шредингера В общем случае основной функцией в этом состоянии является узел.
В общем случае для частицы с полуцелым спином s это положение Подходит для систем, содержащих более 25 + 1 частиц. Для системы Координаты, состоящие из одинаковых бозонов и совершенно симметричные Сильные волновые функции всегда возможны. Z a z h 1. Полностью определить количество уровней энергии с разными значениями Спин S в системе N-частиц со спином 1/2 (Ф. Блох, 1929).
Значение проекции проекции полного спина системы принятия решений M s = cr может быть реализовано N \ 1) Например, существуют следующие пары цепей (когда s = 1): Дополнительные цепи показаны сплошными и пунктирными линиями. Моя линия §63C I M M E T R I O O T N O S N Y Y K P E R E S T A N O V K A M 297 В зависимости от метода (N / 2 + M s назначаются частицы кр = 1/2, а остальные кр = = -1/2).
Соответствует всем домам энергетического уровня с заданным значением S Состояние 2 s + 1 является значением M s = S, S-1. , , -S. Так легко Количество различных уровней с заданным значением S составляет 2 + <S + 1)! (2 Общее количество различных энергетических уровней n = ^ 2 n (S) составляет S n = / (0) = N \ N или n = t-N \ (N + 1 \, [N-1 V 2 J V 2 Нечетное число 7V. 2.
Найти значение общего спина * S, происходящего в разных местах Функция спина симметричной функции 2, 3 или 4 систем Частица 1 со спином. В случае принятия решения двумя частицами соответствие устанавливается следующими фактами. Коэффициент, который умножает спиновую функцию на перестановку Частица должна быть равна (—l) 2s_, s (см. Конец §62).
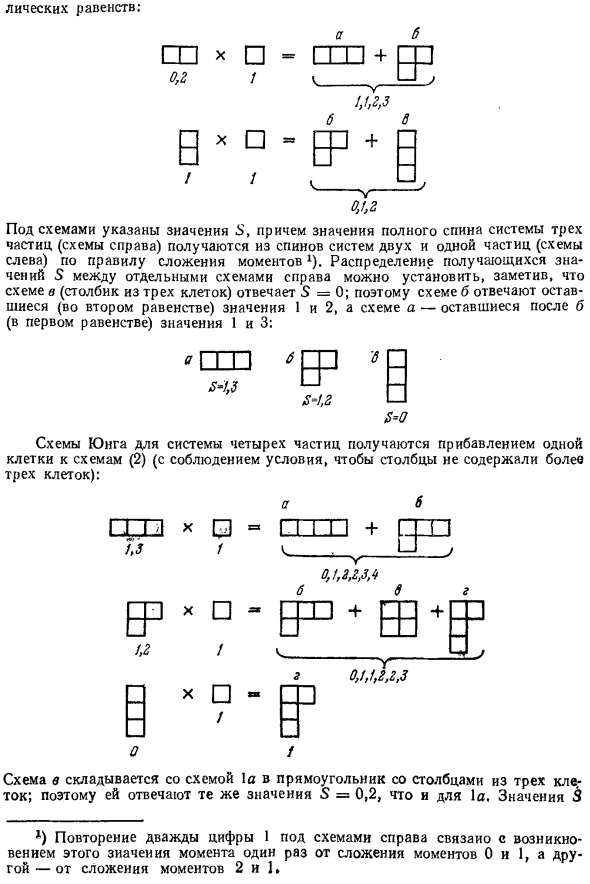
Для частиц со спином s = 1, это дает ответ. <* W b P (1) s = o, 2 U 5 = 1 Схема Юнга для трехчастичной системы Схема одной ячейки (1) всеми возможными способами. Могу написать В форме символического уравнения: w x □ = t p + t 0, 2 1 Y 1, 1, 2, 3 □ = 1 «V 0, 1, 2 Значение S показано ниже схемы, а общее значение вращения системы.
Три частицы wes (правая схема) взяты из двух систем и одного системного спина. Частицы по правилу сложения моментов (рисунок слева) 1). распределение 1) Повторение двузначного числа 1 под правой цифрой Это значение момента от сложения моментов 0 и 1, а также Другое связано с добавлением моментов 2 и 1. 298 Т И О Д Е С Т В Е Н Н О С Т У Ф Х Ц Ч Ш Щ Э Ю IX
Результат значение S м Обновите схему (столбец из 3 ячеек), чтобы она соответствовала S ‘= 0. по Эта схема b соответствует остальным значениям (во втором уравнении) 1 и 2. Значения 1 и 3, оставшиеся после схемы a-b (первое уравнение): 5 = 1,3 S = 1,2 s = o Схема Юнга четырехчастичной системы.
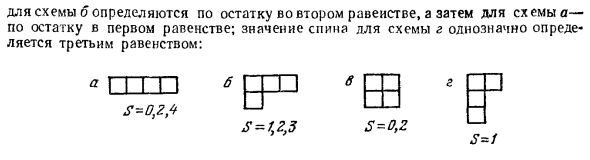
Ячейка для схемы (2) (с учетом критериев, не включенных в столбец Укол 3 или более клеток): 1,3 □ 1 Y 0, 1, 2, 2, 2, 4, 4 EP x p 1, 2 + 0, 1 + 1, 2, 2, 3 г — X □ = 1 0 1 Свернутый вид на рисунке 1а становится трехрядным прямоугольником. Ячейка, поэтому то же значение S = 0,2 соответствует 1а. Другой способ S на схеме b определяется остатком второго уравнения, тогда Для схемы а по оставшейся части первого уравнения. Значение спина схемы r однозначно определяется третьим уравнением.
Смотрите также:
| Принцип неразличимости одинаковых частиц | Вторичное квантование. Случай статистики Бозе |
| Обменное взаимодействие | Вторичное квантование. Случай статистики Ферми |
Если вам потребуется заказать решение по физике вы всегда можете написать мне в whatsapp.

