Оглавление:




Силы взаимодействия молекул. Уравнение состояния неидеального газа
- Теперь необходимо более подробно остановиться на свойствах сил взаимодействия между молекулами. Силы, с помощью которых молекулы (и атомы) действуют друг на друга, могут быть выражены как сумма множества членов, зависящих от свойств взаимодействия молекул. particles. It можно классифицировать следующим образом. 1.Сила, действующая на небольшом расстоянии, то есть сила, которая падает почти до нуля на расстоянии порядка атомных размеров (10″ см).Это, в первую очередь, валентная («химическая») сила. Здесь мы не принимаем во внимание валентную силу.
Тут же принимают очень большое положительное значение, и 2 молекулы соприкасаются друг с другом. Такая грубая идея часто дает подходящее приближение не только для газов, но и для кристаллов. Это связано с тем, что эти силы на определенном расстоянии между частицами очень резко уменьшаются с увеличением distance. In кроме того, для упрощения задачи мы будем рассматривать частицу как ball. In фактически, это подходящее приближение, например, для атома инертного газа.
Если взаимодействующая молекула не имеет постоянного электрического дипольного момента, то сила Ван-дер-Ваальса обусловлена взаимодействием дипольного момента. Людмила Фирмаль
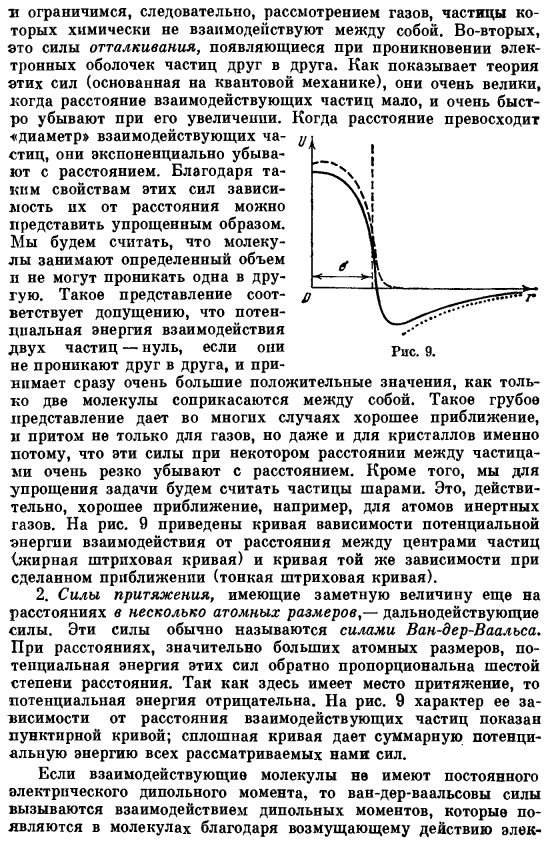
На рисунке 9 показана кривая зависимости потенциального взаимодействия электронов от расстояния между центрами частиц (кривая толстой пунктирной линии) и такая же зависимость от приближения (кривая тонкой пунктирной линии). 2.Сила притяжения, имеющая ярко выраженную величину даже на расстоянии нескольких атомных размеров, является силой больших расстояний. Эти силы обычно называют Ван-дер-Ваальс forces. At на гораздо больших расстояниях, чем атомное измерение, потенциальная энергия этих сил обратно пропорциональна 6-ти степеням расстояния. Поскольку существует гравитационное притяжение, потенциальная энергия отрицательна. Рисунок 9.
Свойства зависимости от расстояния взаимодействующих частиц показаны пунктирной кривой. Сплошная кривая показывает полную потенциальную энергию всех рассматриваемых сил, возникающего в молекуле вследствие возмущающего действия электрического поля. 1. ионы от одной молекулы к другой и 3 электрических поля электронов. Соответствующая энергия взаимодействия пропорциональна квадрату «поляризуемости» молекулы.
Скорость поляризации называется Сила также добавляется к силе взаимодействия дипольного момента, но эти силы обычно меньше силы рассеяния. Рассмотрим силу отталкивания и силу Ван-дер-Ваальса. Зависимость энергии взаимодействия двух частиц от расстояния показана сплошной кривой на рис. 3. 9.Расстояние между центрами частиц, при котором энергия отталкивания начинает резко возрастать, называется диаметром. Рассчитайте величину o (22.5 a), учитывая указанные особенности сил взаимодействия.
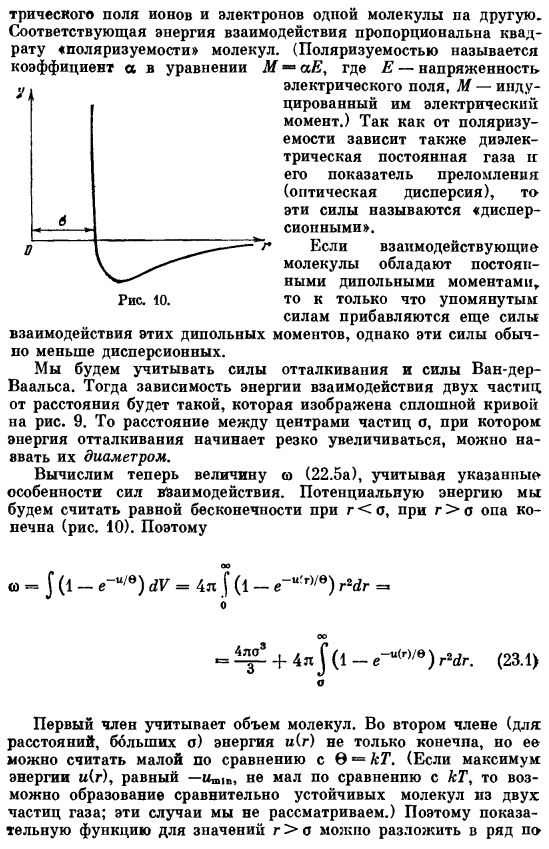
- При r <0 рассмотрим потенциальную энергию, равную Бесконечности. для r> опа конечна(рис. 10)… <о-J в (1-е «» / е) дв = 4л J в(1-e_u р,/ е)’dr Р = = + 4l J(1 _td (23.1) В первом члене учитывается количество молекул. Во 2-м члене (если расстояние o велико) энергия u ® не только конечна, но и может считаться малой по сравнению с 0-kT. (если максимальная энергия u ®, равная-u»ir, не меньше kT, то возможно образование относительно устойчивых молекул из 2 частиц газа.
Эти случаи не рассматриваются.) Следовательно, экспоненциальная функция значения r> a может быть расширена, продолжая Ограничьтесь первой пощечиной: О значении Замена Где мы взяли = — /И / <0 (аттракционы). (23.1).、 Уравнение(23.4) дает уравнение состояния . Среди них 1 из самых успешных-уравнение ван-дер-Вааля. (23.6) Это уравнение состояния только количественно Она совпадает с экспериментальными данными относительно разбавленного газа, но также качественно показывает явление конденсации и перехода в жидкое состояние.
Как известно, для газов предложено большое количество эмпирических уравнений состояния. Людмила Фирмаль
Если число частиц на единицу объема N / V невелико, то можно выразить формулой (23.6), оставив следующий порядок слагаемых. ве /u⁸ П. С. В. М.> В * Если мы сравним это уравнение с (23.4)、 Таким образом, постоянная ван-дер-Ваальса b равна 4-кратному объему молекулы. ОЦР. Разумеется、 Взаимное притяжение сил притяжения всех молекул газа равно среднему пространственному значению энергии. Таким образом, смысл формулы энергии газа(23.5) однозначен.
Его энергия отличается энергией идеального газа и этим количеством. Вычисляя Интеграл состояния, мы рассмотрели проблему реального газа с использованием общих методов. Попробуем более наглядно показать, почему в уравнении состояния появляются дополнительные члены (по сравнению с идеальным газом). При выводе формулы давления газа стенки сосуда используется закон сохранения импульса. С этой точки зрения причины появления коррекции молекулярной массы можно объяснить следующим образом: средний импульс каждой поражающей молекулы определяется температурой и не зависит от объема молекулы.
Однако число молекул, сталкивающихся со стенкой молекулы с конечным объемом, больше, чем число точек, потому что перенос импульса в Газе с конечным объемом происходит в пространстве без молекулы со скоростью теплового движения, а в объеме, занятом молекулой с бесконечной скоростью (мы считаем их трудными с определенной величиной).Учитывая эту ситуацию, мы получаем корректную коррекцию объема*). Если учесть силу притяжения, действующую на частицы газа, прилегающие к стенке от частиц, находящихся в сосуде, как внешнюю силу, то получим поправку, связанную с наличием дальнодействующих forces. In в этом случае потенциал этих сил будет меньше в недрах газа и больше в атмосфере. wall.
Согласно формуле Больцмана, плотность у стенок меньше, чем внутри. Если не учитывать объемную поправку, то стенка Давлепы будет равна формулам Клапейрона U, c. где N-среднее число молекул на единицу объема вблизи стенки. Принимая во внимание разницу между средним числом молекул на единицу объема всего газа, равным этому числу N и N / V, можно получить правильное выражение термина№/К*формулы при тех же допущениях, сделанных в заключении. Государство. • ) Смотрите ниже для получения дополнительной информации. Херцфеловка. Кинематика вещества: Пер.- М.; Л.: ОНТИ, 1935, гл.
Смотрите также:

