Силы в плоскости

Силы в плоскости

• Возьмем плоскость, в которой сила существует относительно плоскости xy. Очевидно, что существуют следующие: З = 0,= = 0,М = 0, ЛК + моя НЗ В. И так оно и есть. При X2H V2 0 система сводится к одному результату в плоскости и ориентируется вдоль центральной оси. Если X = 0, Y = 0 и N 0, система сопряжена. Если X = 0, Y = 0, N = 0, то система находится в равновесии. Если N = 0, то сила, результат действия которой проходит через точку O или находится в equilibrium. So, если сумма моментов силы на 2 точках плоскости равна нулю, то результат пройдет через эти точки или окажется в равновесии.

Наконец, если эта сумма равна нулю в 1 точке плоскости, которая не находится на 3 прямых линиях, то возможно только равновесие. 102.Образцы. 1. возьмите произвольный многоугольник в плоскости xy и приложите силу, пропорциональную длине этой стороны, перпендикулярную ей и направленную к середине каждой стороны на внешней стороне многоугольника. Эти силы уравновешены. Мы докажем это предложение геометрически. Сначала мы делаем это для треугольника, а затем показываем его с помощью ABC рис.68.

Сила, перпендикулярная неподвижной плоскости и являющаяся функцией расстояния от движущейся точки до этой плоскости, имеет силовую функцию. Людмила Фирмаль

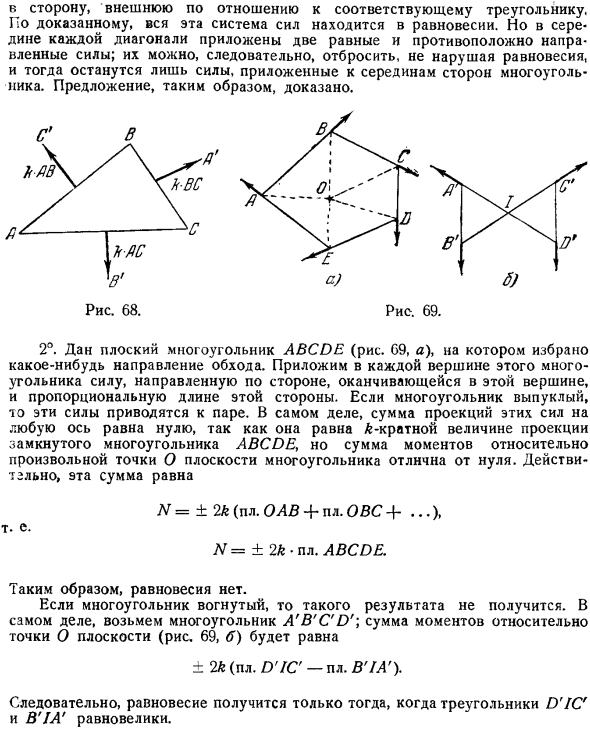
Силы A k BC , B k AC и C k AB пересекаются в 1 точке, как в середине перпендикуляра к стороне Triangle. In кроме того, сумма проекций на любую ось, очевидно, будет равна нулю. Следовательно, эти силы находятся в равновесии. Теперь обратимся к случаю любого многоугольника. Используя диагональ, проведенную из 1 вершины, разделите ее на triangles. In к центру каждой стороны полученного треугольника приложите силу, направленную на сторону b вне соответствующего треугольника, которая пропорциональна длине этой стороны и перпендикулярна к it. As доказано, что вся система этой силы находится в равновесии. Но в центре каждой диагонали приложены 2 равные противоположные силы.

• Поэтому его можно отбросить, не нарушая равновесия, и останется только сила, приложенная к середине стороны многоугольника. Таким образом, предложение доказано. 2.Дан плоский многоугольник ABCDE рис. 69, а, на котором расположены несколько поперечных направлений selected. At к каждой вершине этого многоугольника вы прикладываете силу, направленную вдоль стороны, которая заканчивается в этой вершине и пропорциональна длине этой стороны. Если многоугольник выпуклый, то эти силы равны paired.

Поэтому распределение сил в рассматриваемом поле можно приближенно представить следующим образом. Людмила Фирмаль

Дело в том, что сумма проекций этих сил на любую ось равна нулю, поскольку она равна L раз проекции замкнутого многоугольника ABCDE, но сумма моментов, связанных с любой точкой О плоскости многоугольника, не равна zero. In дело в том, что эта сумма составляет LG = 2L квадрат ODV4 squareOVS4… Иначе говоря Н = 2 ЛП. ABCDE. Следовательно, равновесия нет. Если многоугольник вогнут, этот результат не будет work. In фактически, мы используем полигон a B C D. Сумма моментов относительно точки плоскости O рис. 69, б 2k квадрат D LC квадрат B 1A.

Смотрите также:

Решение задач по теоретической механике

Эквивалентные системы сил	Параллельные силы
Другая форма условий равновесия	Центр тяжести