Оглавление:


Силы постоянного направления. Естественные уравнения
- Предположим, что сила, действующая на точку массы, всегда параллельна некоторой direction. В этом случае траектория находится в плоскости, которая включает начальную скорость и направление силы. Этот результат можно считать ясным из соображений симметрии раздел 202. Возьмите плоскость траектории плоскости xy и укажите ось Oy, параллельную силе.
Установив это, рассмотрим систему точек, подчиненных связям без трения, которые могут быть выражены при помощи равенств. Людмила Фирмаль
И уравнение движения Первое из этих уравнений является х = у б То есть проекция точки на ось Ox движется равномерно вдоль этой оси. Константы a и b определяются из условия, что в t t0 они должны быть x = xy, 1 1 = x, а в самом общем случае 2 м уравнением. формат nie представляет ды ДТ = Ф после замены x формулой + b она преобразуется в следующий вид уравнения: Он идентичен уравнению линейного движения. Если ее удастся интегрировать, проблема будет решена. Естественно equations. In в рассматриваемом случае естественное уравнение упрощается.
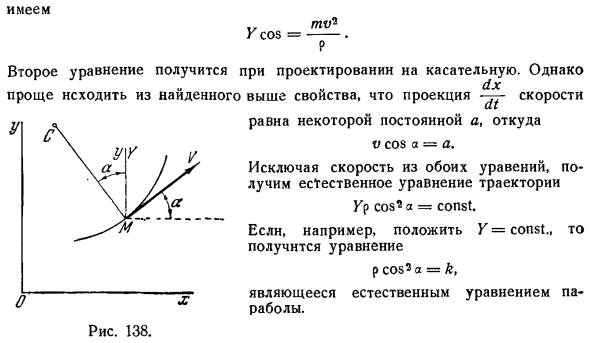
- Возьмите ось прямоугольника. пусть a угол, образованный скоростью с осью Ox рис. 138. Если вы проецируете его на нормальный 2 е уравнение получается при проецировании на касательную. Но дуплексный Проще начать с вышеуказанных свойств. Константа, равная a потому что а = а. Если исключить скорость из обоих уравнений, то получится естественное уравнение траектории ФП cos5 а = сопи Например, y = Конст. И тогда вы получите уравнение П cos5 а к Это естественное уравнение параболы.
Мы изложим здесь классическое доказательство, основанное на анализе различных видов простых связей. Людмила Фирмаль
Мы назвали связанным всякий вектор, приложенный в определенной точйе пространства. исследованием векторного поля,. от них. Эта величина может быть взята, например, равной вириалу Клаузиуса относительно некоторой заданной точки Р. Эта точка называется центром заданной системы, параллельных векторов, связанных со своими точками приложения. называется результирующим вектором системы параллельных связанных векторов.
Смотрите также:
Решение задач по теоретической механике
| Движения под действием силы, зависящей только от скорости | Движение тяжелой точки в пустоте |
| Прямолинейное таутохронное движение | Определение параллельной силы по заданной траектории |

