Оглавление:




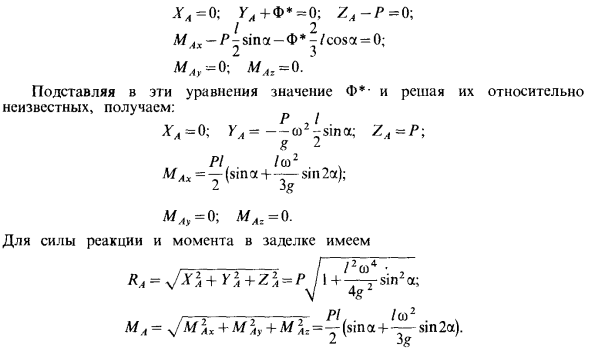

Силы инерции твердого тела в частных случаях его движения
- Поступательное движение. Если твердое тело движется вперед, ускорение в этой точке одинаково. Силы инерции в этих точках составляют систему параллельных сил, направленных в одном направлении. Такая система сил сводится к объединенной силе *. Это равно главному вектору. f ‘= f = -Mac. В этом случае результирующая линия силы инерции проходит через центр тяжести. Это связано с тем, что главный момент инерции каждой точки тела относительно центра тяжести £ ”» = Л ?? С (ПД) = 0.
Фактически, согласно следствиям принципа Даламбера центра тяжести (12) Х л? S (Pe ’) + £? ‘= O Во время перевода тело не вращается вокруг центра тяжести, поэтому X ^ c (A * ‘,) = 0. Следовательно, ££ «= 0. При вращении вокруг неподвижной оси. Если вы выберете точку O центра вращения Oz в качестве центра инерции, то в этой точке будут получены главный вектор и главный момент инерции. Φ = -Wc; L ^ = -dRo / dt. Если центр тяжести находится на оси вращения, Φ = 0. Проекция главного момента инерции на неподвижные оси в общем случае может быть рассчитана по формуле L ™ = -dKx / dt * O. L ™ = -dA ^ / d / ^ O; L ™ = -dKz / dt = -Jzs.
Поступательное движение зависит от выбора точки фигуры, в которой происходит это поступательное движение, но угол поворота вокруг полюсов не зависит от выбора полюса. Людмила Фирмаль
Моменты инерции £ <® * и L1® ‘рассчитываются в следующем разделе. Если оси Oz являются главными осями инерции точки O, они равны нулю. В плоском движении. Если вы выберете центр тяжести в качестве центра уменьшения инерции, вы получите главный вектор и главный момент инерции в этой точке. Для основного вектора силы инерции, F = — форель. Для главного момента инерции относительно центра масс C, который является точкой перемещения плоского движения объекта, получим ту же формулу, что и формулу (14), полученную для неподвижной точки O. Согласно результату принципа Даламбера (12) главный момент инерции относительно центра тяжести удовлетворяет следующему условию £ jWc (Fle>) + Zb® ‘= 0.
С другой стороны, из теоремы относительно изменения момента движения относительно центра тяжести абсолютного и относительного dKc / dt = £ MS (GG); dK? / DT = Из этих отношений £ = -dtfgi / 0; = -dKty / dt ^ 0; L ^ = -dKWdt = -JCle. Здесь ось Cz параллельна плоскости, вдоль которой движется точка тела. Момент инерции рассчитывается так же, как тело вращается вокруг фиксированной оси. Если оси Cz являются главными осями инерции точки C, они равны нулю. Это особенно верно, если тело проходит через центр масс и имеет плоскость симметрии, параллельную плоскости движения тела. Пример I.
- Нагрузка A под действием силы тяжести Pt падает вдоль конца призмы под действием силы тяжести P, а нагрузка B под действием силы тяжести P2 с помощью нити, брошенной на невесомый блок C. При рассмотрении пола сглаживаются края и вес призм, и определяется давление на призмы на полу и выступы, которые препятствуют движению призм и натяжению нитей. Угол наклона стороны призмы воздуха (рис. 84, а, б) Решения. Применимо к системам, состоящим из призм, гирь, нитей и блоков, которые являются результатом принципа Даламбера. Создать равновесие между внешней силой и силой инерции системы.
Предположим, что ускорение груза А направлено вниз и равно а. Для абсолютных значений сил инерции груза А и Б соответственно Уравнение у нас есть Принцип Даламбера PaB «adT ^ yTaS …. Ускорение отдельного груза может быть применено индивидуально к каждому грузу, создавая условие силы инерции в направлении потока. Что получить: условия _ F и F инерция в проекции на координаты S, решение -Pjsmp> 0. Подставляя приобретенную стоимость в (а) Давление призмы за счетчиком будет F «= -F ‘, давление призмы Чтобы определить натяжение нити $, значение ускорения можно рассчитать по формуле (б) или (б) Пример 2.
Системой отсчета для трехмерного евклидова пространства не может служить одна точка, линия или плоскость, необязательно прямая, лежащая в одной плоскости. Людмила Фирмаль
Однородный тонкий стержень АВ Я прочно закреплен на вертикальной оси ГС под углом а (рис. 85, а). Вал ОО вращается вместе со стержнем АВ с постоянной угловой скоростью ω. Определить реакцию стержня на конце А. Решения. Примените результат принципа Даламбера в виде силы равновесия к внешним и инерционным силам стержня AB. Векторные моменты неизвестной реакции RA и конца M1 вытянуты вдоль координатных осей. Если весь стержень разделен на основные секции одинаковой длины, ускорение в каждой точке стержня равно a, = gdsh2, поэтому ускорение в средней точке этих участков линейно распределено вдоль стержня (r равно k Расстояние второй точки) оси вращения.
Силу инерции основного сечения стержня также принимают за точку, распределенную по линейным законам, образующую треугольник. Эти распределенные параллельные силы имеют результирующую силу, линия действия которой находится на расстоянии / s_ / вдоль стержня от основания треугольника и 2/3 / от вершины треугольника. Результирующая сила Ф * всегда равна главному вектору силы, всегда распределенному вдоль треугольника. Для основного вектора силы инерции, F = -масса Штанга, т переменное ускорение Промежуточная точка.
Вот так. Состоит из шести состояний стержня рассматриваемого момента, расположенного в координатной плоскости Айз. Далее проекция силы и ее момента на оси координат Ax, Ay, Az выглядит следующим образом. Рисунок 85 LG4 = O; CL + F * = O; ZA-P = O-, Ml, ~ P-sina-Ф * -Icosa ^ O; Ml = 0; ML = 0. Подстановка значений Ф * в эти уравнения и решение для неизвестных дает: мл = о-, MLg = 0. Для силы реакции и момента уплотнения, Ml = JM Lx + Ml, + M2Lr = ^ — (ma <1 + ˜sin 2a).
Смотрите также:
Задачи по теоретической механике
| Принцип Даламбера для материальной точки | Динамические реакции при вращении твердого тела вокруг неподвижной оси |
| Принцип Даламбера для системы материальных точек | Статическая уравновешенность |

