Оглавление:



Силовой и веревочный многоугольники. Графическое определение равнодействующей для плоской произвольной системы сил
- Мощность и веревочный многоугольник. Одна из проблем со статистикой, как описано в§1.1, состоит в том, чтобы найти любую систему, полученную в результате силы. Эту проблему можно решить, применяя эти силы непрерывно (см.§1.5). Однако этот способ громоздок и неудобен, особенно при применении большого
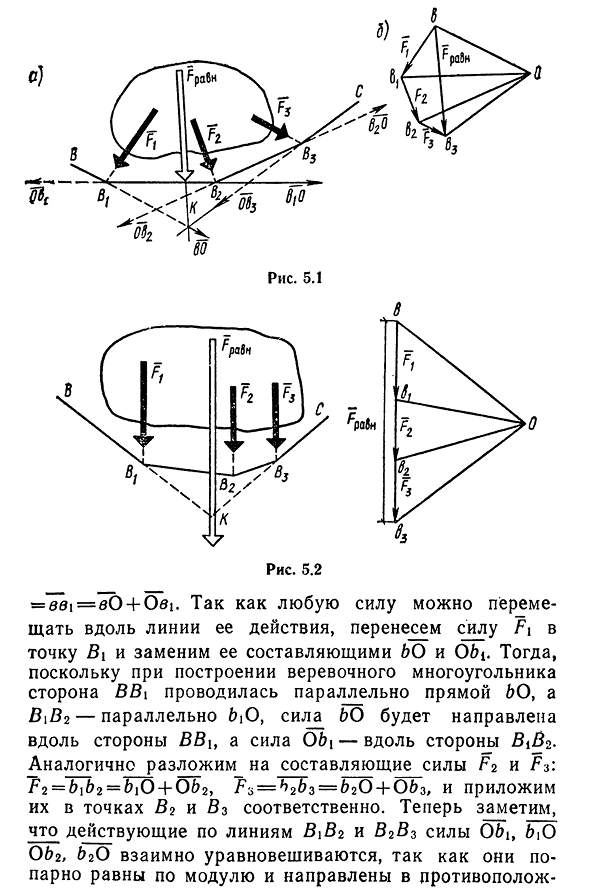
количества сил. Рассмотрим более удобный и простой способ нахождения системы произвольных плоских сил (включая систему параллельных сил). Пусть на свободные твердые тела действует плоская система произвольных сил{Fb F2,F3} (рис. 5.1). Модуль и направление результата этой системы сил определяются правилом силового многоугольника (§1.5).
Давайте теперь выясним положение Людмила Фирмаль
линии действия равнодействующей системы сил. Выталкивает любую точку O, которая не существует на стороне многоугольника или ее продолжение в плоскость многоугольника и соединяет ее со всеми вершинами многоугольника. Затем возьмем любую точку(рис. 5.1, а) провести через нее линию, параллельную линии S, и перейти к точке пересечения с линией действия силы Fi в точке B. Затем
провести линию, параллельную линии, от точки Bi до пересечения с линией действия силы F2 в точке B2, и так далее. Построенная таким образом полилиния BB^b2b3c называется канатным полигоном, и ее название происходит от того, что гибкие нити фиксируются в точках B и C, а нити B2 и B3 фиксируются в точках B и C. Теперь мы докажем, что результирующая линия действия FpaBH фактически проходит
- через точку / S_iz силового многоугольника(рис. 5.1, б) найти, что Fi= 48и = — eei=eb+Oei. Так как любую силу можно перемещать вдоль линии ее действия, то передадим силу Fi в точку Bi, и попробуем заменить составляющие Fi и Obi тогда, так как при построении каната из полигона сторона B I перешла к линии Bo, Bic2-параллельная био сила направляется вдоль стороны Bi и O bi, BI2. Аналогично разложим компоненты силы F2 и F3: F2=bib2=biO+Ob2, F3=h2b3—b2O+Ob3 и приложим их соответственно в 2 и 3 точках.
Теперь сила, действующая на линии b iB2 и B 2b3obi, b, 0Ob2, B 2 o, заключается в том, что модуль равен, и поскольку он направлен в противоположном направлении, он уравновешен друг с другом.- 4-480 Обратная сторона. Поэтому с помощью этих полномочий можно меняться.■ В результате этой системе сил соответствуют две силы
B и obz, направленные вдоль крайних сторон BBI и B3C, а именно канатный многоугольник. {?!, 0-3}. (5.1) Таким образом, через эту Людмила Фирмаль
точку их результат, или то же самое, проходит через результирующий Фпабх системы этой силы. Поскольку полученные правила графического определения являются общими, то применима и система параллельных сил, направленных как на одну, так и на разные стороны. Эти три параллельные силы показаны на рисунке. 5.2
Смотрите также:

