Сила взаимодействия жидкости с поверхностью, движущейся равномерно, поступательно и прямолинейно

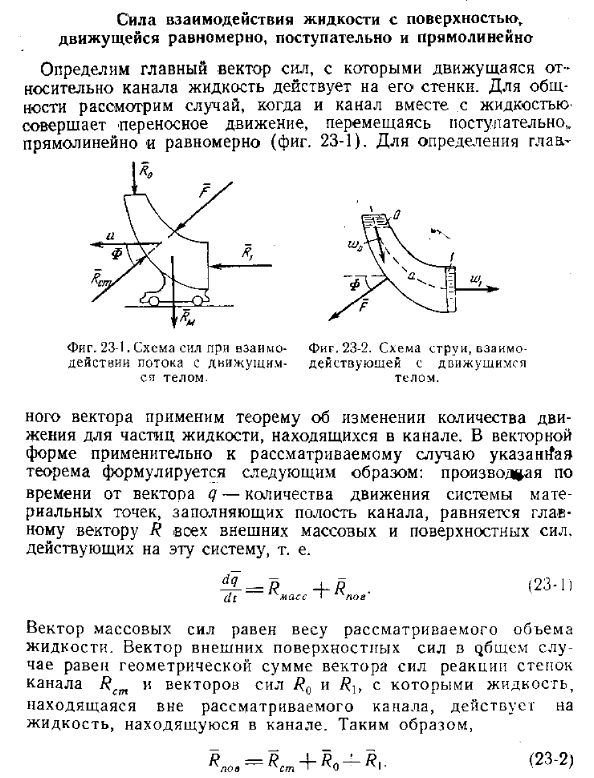
Сила взаимодействия жидкости с поверхностью, движущейся равномерно, поступательно и прямолинейно

Сила взаимодействия жидкости с поверхностью, движущейся равномерно, поступательно и прямолинейно. Определяет основной вектор сил, действующих на стенку при движении жидкости относительно канала. В общем, чтобы определить главу, рассмотрим случай, когда канал движется линейно и равномерно с определенным движением с жидкостью (рис. 23-1).

Результирующая сила давления жидкости на поверхность погруженного в нее твердого тела (выталкивающая сила) равна весу жидкости в объеме погруженной части тела и направлена вверх по вертикали (закон Архимеда) . Людмила Фирмаль

• Для векторов теорема применяется к изменению импульса частиц жидкости в канале. Для векторной формы, применяемой к рассматриваемому случаю, эта теорема формулируется как Импульс системы материальных точек, заполняющих полость временного канала от вектора #, равен главному вектору H всех внешних масс и поверхностных сил, действующих на эту систему, т. е. (23-1) .

Вектор силы массы равен объемному весу рассматриваемой жидкости. Вектор силы внешней поверхности в общем случае равен вектору силы реакции стенки канала $ st и геометрической сумме жидкости Это влияет на жидкость в канале за пределами рассматриваемого канала. Вот так (23-2) • 25 * , ’^ 88 Поток жидкости и взаимодействие твердого тела.

• Чтобы вычислить производную импульса, сначала найдите приращение импульса рассматриваемой системы во время СИ. Пунктирная линия 23-2. Приращение импульса системы рассчитывается как разница между смещением и начальным импульсом. В связи с тем, что канал движется постепенно, этот прирост можно найти как разницу в массообмене при объеме 0 и / или.

Указывает вектор импульса массы жидкости Вы проходите через том 0 и / соответственно? о, яа и р / б Ясно, что импульс рассматриваемой системы в смещенном положении равен геометрической сумме. То же самое относится и к прогрессивной, прямой и равномерной. Следовательно, в течение времени r1 приращение импульса равно _я = я \ <1n ^ 0 рассчитывается.

При определении силового воздействия жидкости на твердую поверхность решают обычно две задачи определяют величину равнодействующей сил гидростатического давления и находят точку ее приложения (центр давления).   Людмила Фирмаль

• В связи с тем, что каналы движутся постепенно, линейно и равномерно, разность импульсов можно рассматривать как разность, соответствующую импульсу только в относительном движении. Таким образом, каждый импульс ^ и можно найти по формуле, аналогичной формуле (10-15). В этой формуле отображается относительная скорость u вместо абсолютной скорости V.

Смотрите также:

Задачи по гидравлике

Возможно эти страницы вам будут полезны:

1. Сопротивление давления.
2. Волновое сопротивление.
3. Сила действия потока жидкости на неподвижное колено, образующее угол 90.
4. Сила действия свободной струи на неподвижную плоскую поверхность.