Сила тяжести и центр тяжести
Материальная точка, отпущенная без начальной скорости вблизи поверхности Земли, совершает движение по отношению к Земле с некоторым ускорением, которое называют ускорением силы тяжести. Это ускорение, измеренное относительно вращающейся Земли, определяется притяжением к центру Земли и вращением Земли вокруг своей оси. Оно оказывается различным на различных широтах и зависит от расстояния точки от оси вращения Земли. Силу, действующую на материальную точку и равную произведению массы этой точки на ускорение силы тяжести, называют весом материальной точки. Направление силы тяжести отличается от направления к центру Земли и изменяется с изменением широты местности. Более детальное изучение силы тяжести будет проведено в динамике.
Рассмотрим систему материальных точек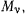 
каждая из которых имеет массу 
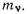Обозначим координаты точки 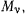через 
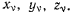Предположим, что на каждую материальную точку действует сила тяжести. Ограничиваясь только случаем, когда размеры тел достаточно малы, будем предполагать, что силы тяжести 
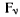всех точек параллельны одному направлению. Очевидно, что если повернуть всю систему на определенный угол, сохраняя взаимное расположение точек, то сами векторы 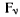не изменят своих величин, а изменят лишь направление по отношению к самой системе материальных точек. Векторы 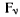в рассматриваемом случае приложены к определенным точкам системы, и следовательно, являются связанными векторами. В теории векторов было показано, что для такой системы векторов существует точка 
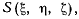координаты которой не зависят от направления векторов и даются уравнениями:
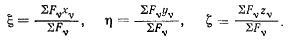
Определенная так точка S называется центром тяжести системы. Она найдена из условия о том, что сумма моментов сил тяжести относительно точки 5 равна нулю. Такая точка будет существовать, поскольку всякая система параллельных сил, направленных в одну сторону, приводится к равнодействующей силе. Аналитически это условие запишется в виде
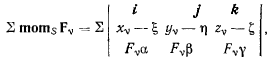
где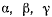 
— направляющие косинусы линии действии силы тяжести относительно выбранных осей координат. Выписанное векторное соотношение эквивалентно трем скалярным уравнениям
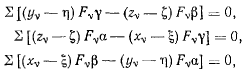
которые можно переписать в виде
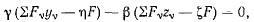
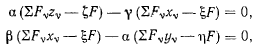
где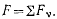 
Полученные из этих уравнений координаты 
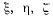определяют произвольную точку, лежащую на линии действия равнодействующей. Положение равнодействующей зависит от направления силы тяжести относительно выбранных осей. Уравнения не будут зависеть от выбора направляющих косинусов 
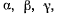если координаты 
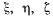удовлетворяют условиям (1), т. е. являются координатами центра тяжести системы. Если систему осей жестко связать с материальными точками, то при изменении положения системы координаты отдельных ее частиц не изменятся, и мы получим способ вычисления координат центра тяжести.
Полученные формулы для координат центра тяжести системы материальных точек не могут быть непосредственно применены к определению центра тяжести сплошных материальных тел. Определение координат центра тяжести в этом случае можно свести к вычислению интегралов.
Действительно, рассмотрим некоторую точку тела, координаты которой обозначим через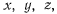 
и выделим из тела элементарный объем 
содержащий эту точку. Будем предполагать, что когда объем стягивается к точке, средняя плотность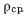 
этого элемента стремится к определенному пределу р, не зависящему от выбора элементарного объема и от способа его стремления к нулю. Величина р представляет собой некоторую функцию от 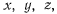которая по своему физическому смыслу однозначна и которую назовем плотностью в точке.
Разделим теперь объем, занимаемый телом, на бесконечно малые элементы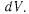 
Масса элемента объема равна 
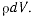Сила тяжести, действующая на элемент 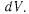может быть представлена в виде
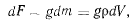
а проекции этой силы на оси координат
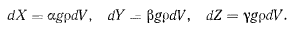
Координаты центра тяжести получат вид
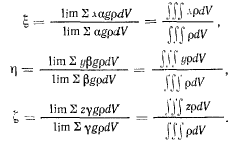
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:
Предмет теоретическая механика
Эти страницы возможно вам будут полезны:
| Частные случаи равновесия твердого тела |
| Задача о равновесии при наличии трения |
| Работа силы на перемещении |
| Сила тяжести |
