Оглавление:



Сила давления жидкости на криволинейные стенки. Плавание тел
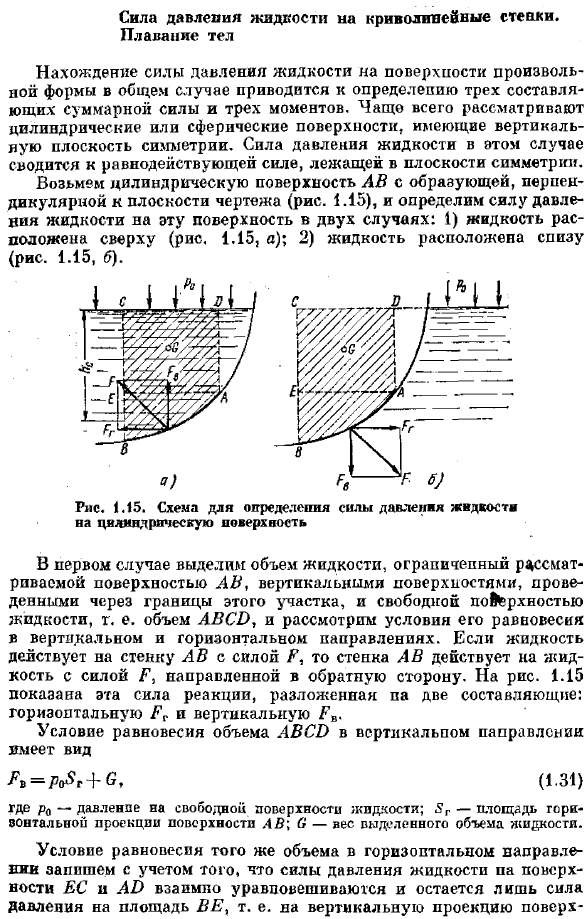
Сила давления жидкости на криволинейные стенки. Плавание тел. Найти давление жидкости на поверхности любой формы в общем случае, это определяет общую силу и 3 составляющие 3 moments. In в большинстве случаев рассмотрим цилиндр или сферу с вертикальной плоскостью симметрии. Давление жидкости в этом случае уменьшается до равнодействующей силы на плоскости симметрии. Возьмем цилиндрическую грань АВ с шиной, перпендикулярной плоскости рисунка (рис. 1.15), и определим силу давления жидкости на эту грань в следующих 2 случаях.1) жидкость находится вверху(рис. 1.15, а). 2) жидкость расположена ниже(Рис. 1.15, б).
В первом случае мы разделяем объем жидкости, ограниченный рассматриваемой поверхностью AB, вертикальную поверхность, проведенную через границы этого сечения, и свободную площадь поверхности R жидкости, то есть объем ABCB, с учетом вертикального и горизонтального состояний равновесия. Рис. 1.15 показана эта сила реакции раскладывается на 2 составляющие: по горизонтали ПГ и по вертикали ПБ. Условие равновесия вертикального объема ABCA является = По $ р-б?(1.31) Где p0-давление свободной поверхности жидкости. Yi площадь горизонтальной проекции поверхности AB \ O-вес разрешенной жидкости.
Если жидкость действует на стенку AB силой, то стенка A B действует на жидкость силой P в противоположном направлении. Людмила Фирмаль
- Давление жидкости на поверхности ЕС и АИ взаимно уравновешиваются и описывают состояние равновесия одного и того же объема в горизонтальном направлении, принимая во внимание тот факт, что в области БЭ остается только давление перпендикулярной проекции поверхности. Двадцать семь бутот АВ-тогда»51prC&C T» Po ^ in * (1.32) При определении вертикальной и горизонтальной составляющих полного давления Р% по формулам (1.31) и (1.32)、 Р = уя + чЕсли жидкость находится ниже (см. рис. 1.15, Б), то гидростатическое давление во всех точках поверхности АВ будет иметь ту же величину, что и в первом случае, но его направление будет противоположным, а суммарные силы Pb и Pm будут определяться по той же формуле (1.31) и (1.32), но использовать обратное sign.
- Кроме того, величину с, как и в первом случае, следует понимать так же, как вес жидкости в объеме АБКО, но этот объем не заполнен жидкостью. Если известна сила Pb и определены центр давления вертикальной проекции стенки и центр тяжести заданного объема ABCB, то положение центра давления цилиндрической стенки можно легко найти. Если цилиндрическая поверхность в вопросе круговая, то задача будет очень easy. In Описанный способ определения силы прижатия цилиндрической поверхности может быть применен также к сфере, в которой результирующая сила проходит через центр поверхности и лежит на симметричной вертикальной плоскости.
Приведенный выше метод нахождения вертикальной составляющей давления жидкости, оказываемого на криволинейную стенку, используется для доказательства закона Архимеда. Погрузите предмет любой формы в объеме V в жидкость(рис. 1.16).Спроецируйте его на свободную поверхность жидкости и нарисуйте цилиндрическую поверхность, которая касается поверхности тела под замкнутой кривой. Эта кривая разделяет верхнюю и нижнюю AT) B поверхности тела ACB. Вертикальная составляющая P1 силы избыточного давления жидкости в верхней части поверхности тела направлена вниз и равна массе жидкости в объеме AA’B’ABA. Вертикальная составляющая Pv2 давления жидкости, оказываемого на нижнюю часть поверхности тела, направлена вверх и равна массе жидкости в объеме AA’B’BVA.
В этом случае все основное давление перпендикулярно поверхности, то есть оно направлено вдоль радиуса, поэтому результирующая сила пересекает ось поверхности. Людмила Фирмаль
- Таким образом, вертикальная равнодействующая сила давления жидкости 28 на корпус направлена вверх, равная весу жидкости объема*, равного разности указанных 2 объемов. RA * = слева O-U 98 * Это закон Архимеда, который обычно формулируется следующим образом: на объект, погруженный в жидкость, действует восходящая плавучесть в вертикальном направлении. Сила РА называется Архимедовой силой, или поддерживающей силой, и точка ее приложения, то есть центр тяжести объема V^, является центром смещения.
В зависимости от отношения массы O к Архимедовой силе RA рассматриваются 3 случая.1) C > RA-тело тонет. 2) О <РА-тело плавает на поверхности жидкости в частично погруженном состоянии. 3) О-РА-тело плавает в полностью погруженном состоянии. Для поддержания равновесия плавающего тела, помимо равенства сил, о-РА должен иметь нулевой суммарный импульс. Последнее условие выполняется, когда центр тяжести тела перпендикулярен центру смещения. Вот условия для устойчивого равновесия плавающих объектов в полностью погруженном состоянии: центр тяжести объекта должен находиться ниже центра смещения. Стабильность баланса тела, растворение.
Смотрите также:
Методические указания по гидравлике
Возможно эти страницы вам будут полезны:

